Bagging や Blending で予測の分散を考慮する

回帰モデルで予測の分散を考慮できるモデルとして、ガウス過程回帰があります。でもあれはあれでけっこうクセがあると思ってて、他の回帰モデルでも予測の分散を考慮できたらなと思ってました。そこで、アンサンブル手法として知られる Bagging や Blending を使えば良いと思ったので試してみました。

予測したい関数

ここでは、単純のため以下のような１変数関数を用います。

import numpy as np

f = lambda x: 0.05*x+0.2*np.sin(x) + 0.3*np.cos(2.1*x) + 0.5*np.sin(0.61*x) + 0.2*np.sin(x/3.1) + 0.1*np.sin(5.1*x)

図示したらこんな感じ。

import matplotlib.pyplot as plt

x_domain = np.linspace(-30, 30, 500) # 関数の範囲
plt.plot(x_domain, f(x_domain))
plt.show()

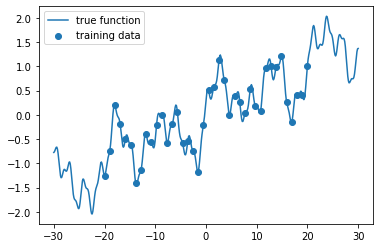
下記のように訓練データを取得して、それを学習させてみたいと思います。

x_train = np.linspace(-20, 20, 40) # 訓練データ

plt.scatter(x_train, f(x_train), label="training data")
plt.plot(x_domain, f(x_domain), label="true function")
plt.legend()
plt.show()

ガウス過程回帰

GaussianProcessRegressor を用いて、予測および予測の分散を求めます。

from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF

kernel = 1.0 * RBF(length_scale=1.0, length_scale_bounds=(1e-1, 10.0))
model = GaussianProcessRegressor(kernel=kernel, random_state=0)
model.fit(x_train.reshape(-1, 1), f(x_train))
y_pred, y_std = model.predict(x_domain.reshape(-1, 1), return_std=True)

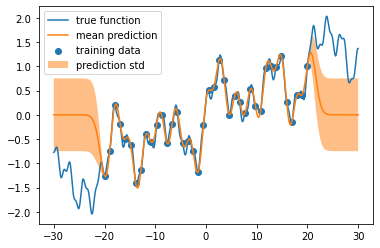
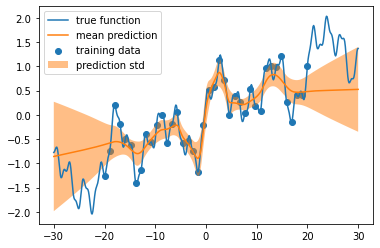
結果の図示

plt.scatter(x_train, f(x_train), label="training data")
plt.plot(x_domain, f(x_domain), label="true function")
plt.plot(x_domain, y_pred, label="mean prediction")
plt.fill_between(x_domain, y_pred-y_std, y_pred+y_std, alpha=0.5, label="prediction std")
plt.legend()
plt.show()

こんな感じで、ガウス過程って、けっこう過剰適合（過学習）しがちで、そのくせ内挿は自信過剰で、外挿はテキトーすぎる印象があるんですよねー（個人の感想です）。

アンサンブル学習器から予測の分散を求める関数

scikit-learnには数多くのアンサンブル学習器が用意されていて、平素より大変お世話になっておりますが、こんな関数が用意されてるともっと嬉しい気がするんです。

def predict_std(model, X):
    y_pred = []
    for base_model in model.estimators_:
        y_pred.append(base_model.predict(X))
    
    return np.array(y_pred).std(axis=0)

Blending

機械学習界隈で「Blending」と呼ばれるアンサンブルは VotingRegressor として実装されています。それを使って、たとえば MLPRegressor をアンサンブルしてみます。

from sklearn.ensemble import VotingRegressor
from sklearn.neural_network import MLPRegressor

model = VotingRegressor(
    estimators = [(str(x), 
                   MLPRegressor(
                       hidden_layer_sizes=[100 for x in range(10)],
                       max_iter=1000,
                       #early_stopping=True
                       )
    ) for x in range(100)]
)

model.fit(x_train.reshape(-1, 1), f(x_train))
y_pred = model.predict(x_domain.reshape(-1, 1))
y_std = predict_std(model, x_domain.reshape(-1, 1))

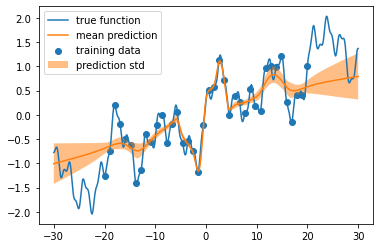
図示すると次のようになります。うーん、まだ不十分な感じだけど、ガウス過程回帰よりは、良いんじゃないですかね。

plt.scatter(x_train, f(x_train), label="training data")
plt.plot(x_domain, f(x_domain), label="true function")
plt.plot(x_domain, y_pred, label="mean prediction")
plt.fill_between(x_domain, y_pred-y_std, y_pred+y_std, alpha=0.5, label="prediction std")
plt.legend()
plt.show()

MLPRegressorには、過剰適合を防ぐ early_stopping=True というオプションがあるのですが、それを入れるとさらにザックリとした予測になります。

Bagging

次は Bagging です。

from sklearn.ensemble import BaggingRegressor
from sklearn.neural_network import MLPRegressor

model = BaggingRegressor(
    base_estimator=MLPRegressor(
        hidden_layer_sizes=[100 for x in range(10)],
        max_iter=1000,
        #early_stopping=True
        ),
    n_estimators=100
    )

model.fit(x_train.reshape(-1, 1), f(x_train))
y_pred = model.predict(x_domain.reshape(-1, 1))
y_std = predict_std(model, x_domain.reshape(-1, 1))

結果の図示

plt.scatter(x_train, f(x_train), label="training data")
plt.plot(x_domain, f(x_domain), label="true function")
plt.plot(x_domain, y_pred, label="mean prediction")
plt.fill_between(x_domain, y_pred-y_std, y_pred+y_std, alpha=0.5, label="prediction std")
plt.legend()
plt.show()

うん、このくらいが一番良い気がしますね（個人の感想です）。