山を登る時、ルートもわからん！頂上がどこにあるかもわからんでは遭難は確実なんじゃ！

プログラミングの勉強を始める時、最初はとても退屈で苦痛です。

まず実行環境を整えなければなりません。初心者はそこでつまづきます。たいていはここで、熟練者の助けが必要になります。

さて、何とか実行環境が整ったら、次はプログラミング言語の文法を勉強します。ところがその作業は非常に退屈で苦痛です。

「そもそもプログラミング勉強したら、何ができるようになるの？」

それを理解するためには、プログラミングを勉強しなければいけないというデッドロック。

「山を登る時、ルートもわからん！頂上がどこにあるかもわからんでは遭難は確実なんじゃ！」

そう、これはPythonの勉強に限らず、コーラを飲んだらゲップが出るっていうくらい確実な宇宙の普遍的法則というべきでしょう。

そうなんですねー。

Python で遭難しないために

Python を使うと、いろんなことができます。色々すぎて説明しきれません。そこで、たくさんある「頂上」のひとつをここでお見せしたいと思います。まずは、意味がわからなくても構いませんので、「コピペ」で頂上まで登ってみてください。以下のコードは全て Google Colaboratory という実行環境での使用を想定しています。

まずは、図を描画するときに日本語を使えるようにするための呪文を唱えておきます。

!pip install japanize-matplotlib

Collecting japanize-matplotlib
[?25l  Downloading https://files.pythonhosted.org/packages/aa/85/08a4b7fe8987582d99d9bb7ad0ff1ec75439359a7f9690a0dbf2dbf98b15/japanize-matplotlib-1.1.3.tar.gz (4.1MB)
[K     |████████████████████████████████| 4.1MB 3.4MB/s 
[?25hRequirement already satisfied: matplotlib in /usr/local/lib/python3.7/dist-packages (from japanize-matplotlib) (3.2.2)
Requirement already satisfied: numpy>=1.11 in /usr/local/lib/python3.7/dist-packages (from matplotlib->japanize-matplotlib) (1.19.5)
Requirement already satisfied: pyparsing!=2.0.4,!=2.1.2,!=2.1.6,>=2.0.1 in /usr/local/lib/python3.7/dist-packages (from matplotlib->japanize-matplotlib) (2.4.7)
Requirement already satisfied: python-dateutil>=2.1 in /usr/local/lib/python3.7/dist-packages (from matplotlib->japanize-matplotlib) (2.8.1)
Requirement already satisfied: cycler>=0.10 in /usr/local/lib/python3.7/dist-packages (from matplotlib->japanize-matplotlib) (0.10.0)
Requirement already satisfied: kiwisolver>=1.0.1 in /usr/local/lib/python3.7/dist-packages (from matplotlib->japanize-matplotlib) (1.3.1)
Requirement already satisfied: six>=1.5 in /usr/local/lib/python3.7/dist-packages (from python-dateutil>=2.1->matplotlib->japanize-matplotlib) (1.15.0)
Building wheels for collected packages: japanize-matplotlib
  Building wheel for japanize-matplotlib (setup.py) ... [?25l[?25hdone
  Created wheel for japanize-matplotlib: filename=japanize_matplotlib-1.1.3-cp37-none-any.whl size=4120276 sha256=f1117e17562a3146802c6bf230ed7c2f5db395b38a791ca1b7881a1ad4d72573
  Stored in directory: /root/.cache/pip/wheels/b7/d9/a2/f907d50b32a2d2008ce5d691d30fb6569c2c93eefcfde55202
Successfully built japanize-matplotlib
Installing collected packages: japanize-matplotlib
Successfully installed japanize-matplotlib-1.1.3

ケーススタディ１：家賃

家賃のデータを解析します。

データ取得

まずは、データの取得を行います。

import urllib.request 

url = "https://raw.githubusercontent.com/maskot1977/toydata/main/home.txt"
urllib.request.urlretrieve(url, 'data.txt')

('data.txt', <http.client.HTTPMessage at 0x7f010d549090>)

家賃のデータの中身はこんな感じです。

import pandas as pd

df = pd.read_csv('data.txt', delimiter="\t")
df

	家賃（円）	徒歩（分）	専有面積（㎡）	築年数（年）	階数（階）	新築	2階以上	南向き	駐車場	オートロック	エアコン	バストイレ別	追い焚き	フローリング	ペット相談可
0	88500	10	20.70	3	8	0	1	0	1	1	1	1	0	1	1
1	86700	10	20.70	3	7	0	1	1	1	1	1	1	0	1	1
2	87300	10	20.70	3	2	0	1	1	1	1	1	1	0	1	1
3	88200	10	20.70	3	9	0	1	1	1	1	1	1	0	1	1
4	170000	10	41.40	3	11	0	1	1	1	1	1	1	1	1	1
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
95	88000	8	21.29	10	4	0	1	0	0	1	1	1	0	1	1
96	88000	8	20.58	10	5	0	1	0	0	1	1	1	0	1	1
97	88000	8	22.04	10	9	0	1	0	0	1	1	1	0	1	0
98	88000	8	20.58	10	8	0	1	0	0	1	1	1	0	0	0
99	93000	7	22.50	7	2	0	1	0	0	1	1	1	0	1	0

100 rows × 15 columns

散布図

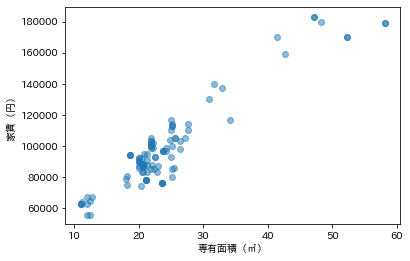
占有面積を横軸に、家賃を縦軸にして散布図を描いてみましょう。明らかな相関があることが分かります。

import matplotlib.pyplot as plt
import japanize_matplotlib 

plt.scatter( df['専有面積（㎡）'], df['家賃（円）'], alpha=0.5)
plt.xlabel('専有面積（㎡）')
plt.ylabel('家賃（円）')
plt.show()

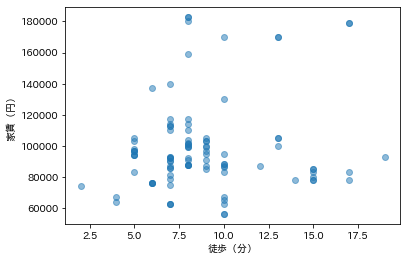
主要駅からの距離が、家賃に影響するかどうか調べてみましょう。駅に近ければ近いほど高い、というわけではなさそうです。

import matplotlib.pyplot as plt

plt.scatter(df['徒歩（分）'], df['家賃（円）'], alpha=0.5)
plt.xlabel('徒歩（分）')
plt.ylabel('家賃（円）')
plt.show()

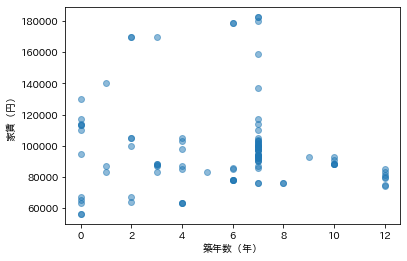
築年数との関係も調べてみましょう。ある程度以上古くなると安くなるものの、そんなに簡単な関係ではなさそうですね。

import matplotlib.pyplot as plt

plt.scatter(df['築年数（年）'], df['家賃（円）'], alpha=0.5)
plt.xlabel('築年数（年）')
plt.ylabel('家賃（円）')
plt.show()

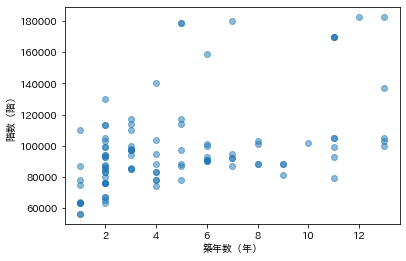
何階建ての建物かと、家賃との関係も、緩やかな相関はあるかもしれませんが単純な話ではなさそうです。

import matplotlib.pyplot as plt

plt.scatter(df['階数（階）'], df['家賃（円）'], alpha=0.5)
plt.xlabel('築年数（年）')
plt.ylabel('階数（階）')
plt.show()

これまでに調べた関係をまとめて図示すると次のようになります。

import matplotlib.pyplot as plt
import japanize_matplotlib 

pd.plotting.scatter_matrix(df.iloc[:, :5], figsize=(8, 8)) 
plt.show()

ヒストグラム

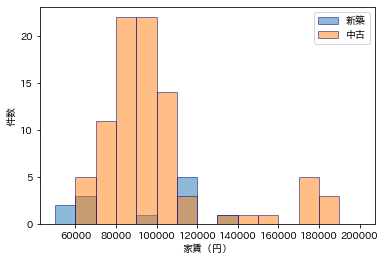
次に、１か０か（２択）しかない属性との関係を調べてみましょう。まず、新築かどうかです。新築なら家賃が高いかと言われると、どうもそういう話ではなさそうです。

plt.hist(df[df['新築'] == 1]['家賃（円）'], alpha=0.5, label="新築", ec='navy', bins=15, range=(50000, 200000))
plt.hist(df[df['新築'] == 0]['家賃（円）'], alpha=0.5, label="中古", ec='navy', bins=15, range=(50000, 200000))
plt.legend()
plt.xlabel('家賃（円）')
plt.ylabel('件数')
plt.show()

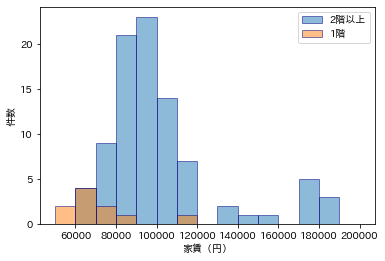
１階かどうかは、家賃とかなり関係がありそうですね。

plt.hist(df[df['2階以上'] == 1]['家賃（円）'], alpha=0.5, label="2階以上", ec='navy', bins=15, range=(50000, 200000))
plt.hist(df[df['2階以上'] == 0]['家賃（円）'], alpha=0.5, label="1階", ec='navy', bins=15, range=(50000, 200000))
plt.legend()
plt.xlabel('家賃（円）')
plt.ylabel('件数')
plt.show()

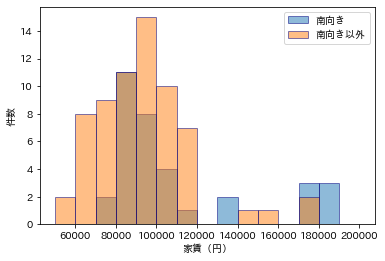
南向きかどうかは、あまり関係なさそうに見えますね。

plt.hist(df[df['南向き'] == 1]['家賃（円）'], alpha=0.5, label="南向き", ec='navy', bins=15, range=(50000, 200000))
plt.hist(df[df['南向き'] == 0]['家賃（円）'], alpha=0.5, label="南向き以外", ec='navy', bins=15, range=(50000, 200000))
plt.legend()
plt.xlabel('家賃（円）')
plt.ylabel('件数')
plt.show()

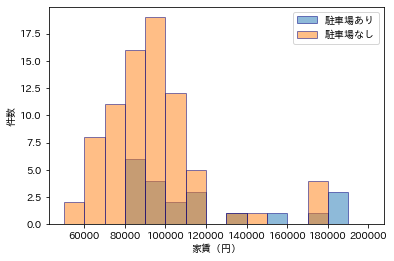
駐車場付きの物件は高めになる傾向がありそうです。

plt.hist(df[df['駐車場'] == 1]['家賃（円）'], alpha=0.5, label="駐車場あり", ec='navy', bins=15, range=(50000, 200000))
plt.hist(df[df['駐車場'] == 0]['家賃（円）'], alpha=0.5, label="駐車場なし", ec='navy', bins=15, range=(50000, 200000))
plt.legend()
plt.xlabel('家賃（円）')
plt.ylabel('件数')
plt.show()

オートロックがついてるかどうかですが...うーん、このデータは本当に正しいのかな？と個人的には疑っています。

plt.hist(df[df['オートロック'] == 1]['家賃（円）'], alpha=0.5, label="オートロックあり", ec='navy', bins=15, range=(50000, 200000))
plt.hist(df[df['オートロック'] == 0]['家賃（円）'], alpha=0.5, label="オートロックなし", ec='navy', bins=15, range=(50000, 200000))
plt.legend()
plt.xlabel('家賃（円）')
plt.ylabel('件数')
plt.show()

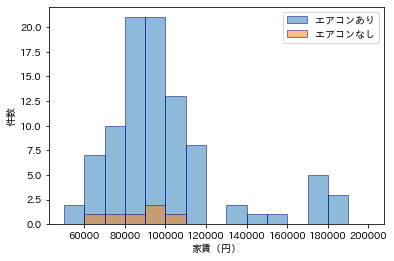
今の時代、エアコンがあるのが普通で、エアコンのない物件は安いようですね。

plt.hist(df[df['エアコン'] == 1]['家賃（円）'], alpha=0.5, label="エアコンあり", ec='navy', bins=15, range=(50000, 200000))
plt.hist(df[df['エアコン'] == 0]['家賃（円）'], alpha=0.5, label="エアコンなし", ec='navy', bins=15, range=(50000, 200000))
plt.legend()
plt.xlabel('家賃（円）')
plt.ylabel('件数')
plt.show()

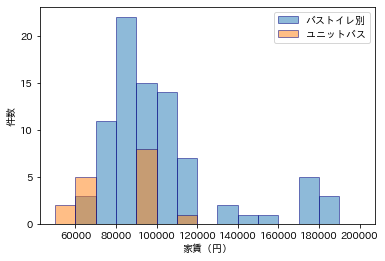
バストイレ別についても同様。

plt.hist(df[df['バストイレ別'] == 1]['家賃（円）'], alpha=0.5, label="バストイレ別", ec='navy', bins=15, range=(50000, 200000))
plt.hist(df[df['バストイレ別'] == 0]['家賃（円）'], alpha=0.5, label="ユニットバス", ec='navy', bins=15, range=(50000, 200000))
plt.legend()
plt.xlabel('家賃（円）')
plt.ylabel('件数')
plt.show()

追い焚きがついてる物件は高めになるようです。

plt.hist(df[df['追い焚き'] == 1]['家賃（円）'], alpha=0.5, label="追い焚きあり", ec='navy', bins=15, range=(50000, 200000))
plt.hist(df[df['追い焚き'] == 0]['家賃（円）'], alpha=0.5, label="追い焚きなし", ec='navy', bins=15, range=(50000, 200000))
plt.legend()
plt.xlabel('家賃（円）')
plt.ylabel('件数')
plt.show()

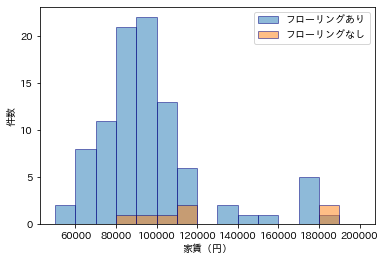
フローリングは、あるのが普通で、うーん、この分布はどう解釈すればいいんだ。

plt.hist(df[df['フローリング'] == 1]['家賃（円）'], alpha=0.5, label="フローリングあり", ec='navy', bins=15, range=(50000, 200000))
plt.hist(df[df['フローリング'] == 0]['家賃（円）'], alpha=0.5, label="フローリングなし", ec='navy', bins=15, range=(50000, 200000))
plt.legend()
plt.xlabel('家賃（円）')
plt.ylabel('件数')
plt.show()

ペット相談可かどうかは、意外と、家賃との関係はなさそうに見えます。

plt.hist(df[df['ペット相談可'] == 1]['家賃（円）'], alpha=0.5, label="ペット相談可", ec='navy', bins=15, range=(50000, 200000))
plt.hist(df[df['ペット相談可'] == 0]['家賃（円）'], alpha=0.5, label="ペット相談不可", ec='navy', bins=15, range=(50000, 200000))
plt.legend()
plt.xlabel('家賃（円）')
plt.ylabel('件数')
plt.show()

以上の話は、賃貸物件に詳しい方が見れば、ツッコミどころが多いかもしれません。私は賃貸の専門家ではありませんので、すみません。とりあえず、データ解析の例をお見せしてみました。

回帰直線

解析をさらに進めてみましょう。次は「回帰直線」です。家賃が占有面積と強い正の相関があることがわかったので、占有面積から家賃を予測する回帰直線を描いてみましょう。

import matplotlib.pyplot as plt
import japanize_matplotlib 
from sklearn import linear_model

model = linear_model.LinearRegression()
model.fit(df['専有面積（㎡）'].values.reshape(len(df),1), df['家賃（円）'].T) # 予測モデルを作成
plt.scatter( df['専有面積（㎡）'], df['家賃（円）'], alpha=0.5)
plt.plot(df['専有面積（㎡）'], model.predict(df['専有面積（㎡）'].values.reshape(100,1)))
plt.xlabel('専有面積（㎡）')
plt.ylabel('家賃（円）')
plt.show()

この回帰直線が、南向き物件か否かで、どう違ってくるか調べてみましょう。

import matplotlib.pyplot as plt
import japanize_matplotlib 
from sklearn import linear_model

df1 = df[df['南向き'] == 1]
df2 = df[df['南向き'] == 0]

model1 = linear_model.LinearRegression()
model1.fit(df1['専有面積（㎡）'].values.reshape(len(df1),1), df1['家賃（円）'].T) # 予測モデルを作成
plt.scatter(df1['専有面積（㎡）'], df1['家賃（円）'], alpha=0.8)
plt.plot(df1['専有面積（㎡）'], model1.predict(df1['専有面積（㎡）'].values.reshape(len(df1),1)), label="南向き")

model2 = linear_model.LinearRegression()
model2.fit(df2['専有面積（㎡）'].values.reshape(len(df2),1), df2['家賃（円）'].T) # 予測モデルを作成
plt.scatter(df2['専有面積（㎡）'], df2['家賃（円）'], alpha=0.8)
plt.plot(df2['専有面積（㎡）'], model2.predict(df2['専有面積（㎡）'].values.reshape(len(df2),1)), label="南向き以外")

plt.xlabel('専有面積（㎡）')
plt.ylabel('家賃（円）')
plt.legend()
plt.show()

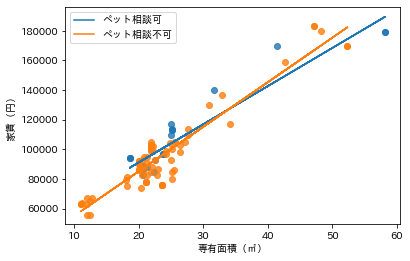
ペット相談可能物件かどうかで比べてみましょう。

import matplotlib.pyplot as plt
import japanize_matplotlib 
from sklearn import linear_model

df1 = df[df['ペット相談可'] == 1]
df2 = df[df['ペット相談可'] == 0]

model1 = linear_model.LinearRegression()
model1.fit(df1['専有面積（㎡）'].values.reshape(len(df1),1), df1['家賃（円）'].T) # 予測モデルを作成
plt.scatter(df1['専有面積（㎡）'], df1['家賃（円）'], alpha=0.8)
plt.plot(df1['専有面積（㎡）'], model1.predict(df1['専有面積（㎡）'].values.reshape(len(df1),1)), label="ペット相談可")

model2 = linear_model.LinearRegression()
model2.fit(df2['専有面積（㎡）'].values.reshape(len(df2),1), df2['家賃（円）'].T) # 予測モデルを作成
plt.scatter(df2['専有面積（㎡）'], df2['家賃（円）'], alpha=0.8)
plt.plot(df2['専有面積（㎡）'], model2.predict(df2['専有面積（㎡）'].values.reshape(len(df2),1)), label="ペット相談不可")

plt.xlabel('専有面積（㎡）')
plt.ylabel('家賃（円）')
plt.legend()
plt.show()

さて、問題は、これらの結果をどう解釈するかですけれども。占有面積や家賃の分布は一様ではなくて、２５平米、１０万円付近に固まった分布をしているので、解釈は慎重にしたほうがいいような気がします。

ケーススタディ２：偽札

次のデータは、ある紙幣の縦の長さ、横の長さなどを計測したものです。

データ取得

import urllib.request 

url = "https://raw.githubusercontent.com/maskot1977/ipython_notebook/master/toydata/sbnote_dataJ.txt"
urllib.request.urlretrieve(url, 'data.txt')

('data.txt', <http.client.HTTPMessage at 0x7f00f9d5ca50>)

import pandas as pd
df = pd.read_csv('data.txt', delimiter="\t")
data = df.iloc[:, :-1]
target = df['class']
data

	length	left	right	bottom	top	diagonal
0	214.8	131.0	131.1	9.0	9.7	141.0
1	214.6	129.7	129.7	8.1	9.5	141.7
2	214.8	129.7	129.7	8.7	9.6	142.2
3	214.8	129.7	129.6	7.5	10.4	142.0
4	215.0	129.6	129.7	10.4	7.7	141.8
...	...	...	...	...	...	...
195	215.0	130.4	130.3	9.9	12.1	139.6
196	215.1	130.3	129.9	10.3	11.5	139.7
197	214.8	130.3	130.4	10.6	11.1	140.0
198	214.7	130.7	130.8	11.2	11.2	139.4
199	214.3	129.9	129.9	10.2	11.5	139.6

200 rows × 6 columns

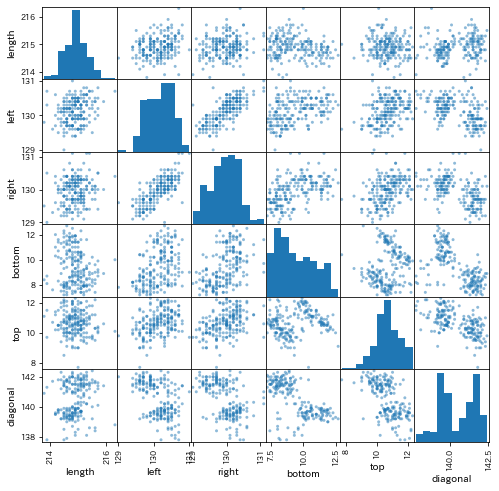
散布図

分布を見てみましょう。すると、どうやらこの紙幣は２つのグループから成るように見えます。

pd.plotting.scatter_matrix(data, figsize=(8, 8)) 
plt.show()

正解ラベル

実際その通りで、本物の紙幣と、偽物の紙幣（偽札）が混じったデータになります。本物か偽物かで色分けすると、次のようになります（どっちがどの色か忘れました）。

pd.plotting.scatter_matrix(data, figsize=(8, 8), c=list(target)) 
plt.show()

教師なし機械学習

では、本物か偽物かを区別する方法は作れないものでしょうか？いくつか方法はあります。一つは「教師なし機械学習」と呼ばれる手法で、クラスターというグループに自動で分割する手法です。その中で「k-means」という手法を試してみましょう。

from sklearn.cluster import KMeans 

kmeans_model = KMeans(n_clusters = 2).fit(data)
pd.plotting.scatter_matrix(data, figsize=(8, 8), c=kmeans_model.labels_) 
plt.show()

同じような結果が得られましたね。k-meansによる分類と、実際の正解データがどのくらい違うのか、混合行列を計算してみましょう。

from sklearn.metrics import confusion_matrix # 混合行列

# 予測結果と、正解（本当の答え）がどのくらい合っていたかを表す混合行列
pd.DataFrame(confusion_matrix(kmeans_model.labels_, list(target)), index=['predicted 0', 'predicted 1'], columns=['real 0', 'real 1'])

	real 0	real 1
predicted 0	100	0
predicted 1	0	100

なんと、完全一致でした。

教師あり機械学習

次に、「教師あり機械学習」の一種である「ロジスティック回帰」を使ってみたいと思います。先程の「K-mean」では、「正解ラベル（本物か偽物か）」の情報を用いずに分類したのに対して、以下の「ロジスティック回帰」では、「正解ラベル（本物か偽物か）」の情報を用いて分類します。

from sklearn.linear_model import LogisticRegression # ロジスティック回帰
model = LogisticRegression(max_iter=530000) #モデルの生成
model.fit(data, list(target))
pd.plotting.scatter_matrix(data, figsize=(8, 8), c=model.predict(data)) 
plt.show()

from sklearn.metrics import confusion_matrix # 混合行列

# 予測結果と、正解（本当の答え）がどのくらい合っていたかを表す混合行列
pd.DataFrame(confusion_matrix(model.predict(data), list(target)), index=['predicted 0', 'predicted 1'], columns=['real 0', 'real 1'])

	real 0	real 1
predicted 0	99	0
predicted 1	1	100

惜しい！１個だけ、外してしまいました。

以上の解析結果は、ロジスティック回帰よりもk-meansのほうが優れている、ということではありません。データの分布の形によって、どの手法が適しているかは変わります。

終わりに

以上、プログラミング初学者が陥りがちな「プログラミングで何ができるの？」というデッドロックを回避するために、ケーススタディを２つお見せしました。最初は「コピペ」だけで大丈夫です。「頂上」（何ができるか）がイメージできたら、次は、その詳細を理解したり、個別の目的のために改変したりできるように「ルート」を進んでいきましょう。