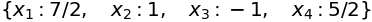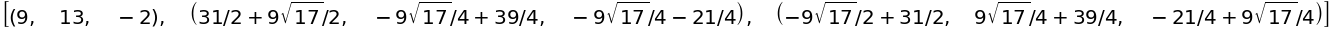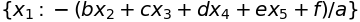連立一次方程式を解くライブラリ
連立一次方程式の解法は、プログラミング演習の題材として非常によく使われますが、実用上は、強力なライブラリが多数存在しますので、自作するよりも既存のライブラリを使ったほうが便利です。
ただし、連立一次方程式の解法を理解しておくということも大事ですし、また、連立一次方程式の解法を実装することはプログラミングの勉強にはとても良いです。
まずは、強力なライブラリ群を紹介してその使い方を習得しましょう。
Sympy を使う方法
Sympyは、代数計算を行うライブラリです。
import sympy
複雑な数式でも図示できるような呪文を唱えます。
sympy.init_printing()
数式を扱う際に、用いる記号をあらかじめ宣言します。
x1, x2, x3, x4 = sympy.symbols('x1 x2 x3 x4')
たとえば、連立方程式
3 x1 + 2 x2 + 7 x3 + x4 = 8
x1 + 5 x2 + x3 - x4 = 5
4 x1 + x2 + 3 x3 - 2 x4 = 7
x1 + 6 x2 + 4 x3 + 3 x4 = 13
は次のようにして解きます。
sympy.solve([3 * x1 + 2 * x2 + 7 * x3 + x4 - 8,
x1 + 5 * x2 + x3 - x4 - 5,
4 * x1 + x2 + 3 * x3 - 2 * x4 - 7,
x1 + 6 * x2 + 4 * x3 + 3 * x4 - 13], [x1, x2, x3, x4])
重解があっても何とかなります。
sympy.solve([x1 + x2 + x3 - 20,
x1 * x2 * x3 + 234,
2 * x1 + 5 * x2 - x3 - 85], [x1, x2, x3])
方程式の解を求めるだけではなくて、与えられた等式を任意の変数について解け、ということもやってくれます。
a, b, c, d, e, f = sympy.symbols('a b c d e f')
sympy.solve([a * x1 + b * x2 + c * x3 + d * x4 + e * x5 + f], [x1])
まあ便利。
Numpy.ligalg や Scipy.linalg を使う方法
NumpyでもScipyでも、連立方程式関係のモジュールが用意されています。まず、連立方程式
3 x1 + 2 x2 + 7 x3 + x4 = 8
x1 + 5 x2 + x3 - x4 = 5
4 x1 + x2 + 3 x3 - 2 x4 = 7
x1 + 6 x2 + 4 x3 + 3 x4 = 13
を次のように表現します。
import numpy as np
A = np.array([
[3, 2, 7, 1],
[1, 5, 1, -1],
[4, 1, 3, -2],
[1, 6, 4, 3]
])
b = np.array([8, 5, 7, 13])
Numpy.linalg を使う方法 (1)
Numpy には連立一次方程式を解く専用の関数が用意されています。
x = np.linalg.solve(A, b)
print(x)
[ 3.5 1. -1. 2.5]
Numpy.linalg を使う方法 (2)
なんなら、Aの逆行列を求めてから、bとの内積をとってもいいです。
Ainv = np.linalg.inv(A) # A の逆行列を計算
x = np.dot(Ainv, b) # A の逆行列と b の内積
print(x)
[ 3.5 1. -1. 2.5]
Scipy.linalg を使う方法
Scipy にも連立一次方程式を解く専用の関数が用意されています。
from scipy import linalg
LU = linalg.lu_factor(A)
x = linalg.lu_solve(LU, b)
print(x)
[ 3.5 1. -1. 2.5]
連立一次方程式の解法
連立一次方程式の解法は、反復法と直接法の2つに大別されます。それぞれどのような方法なのか、どう違うのか、ググって調べてみましょう。
反復法
ヤコビ(Jacobi)法、ガウス・ザイデル(Gauss-Seidel)法、逐次加速緩和法(SOR法: Successive Over-Relaxation)など。
直接法
LU(Lower triangular matrix / Upper triangular matrix)分解法、Gaussの消去法、掃き出し法、Gauss-Jordan法など
線形重回帰
線形単回帰を Python で理解するでは、sklearnを使った線形単回帰と、sklearnを使わない線形単回帰を勉強しました。線形単回帰は説明変数が1つの場合です。それでは、線形重回帰(説明変数が2つ以上の場合)はどう計算するのでしょうか?
説明変数が2つの場合
y = a0 + a1 * x1 + a2 * x2
は、以下のような解法が存在します。
a1 = x2 の影響を除いた x1 と y の偏回帰係数 (partial regression coefficient)
a2 = x1 の影響を除いた x2 と y の偏回帰係数 (partial regression coefficient)
a0 = average(y) - a1 * average(x1) - a2 * average(x2)
説明変数が3つ以上になると、連立方程式を使って解きます(説明変数が2つの場合でも連立方程式を使って解けます)。
線形重回帰と連立方程式
線形重回帰における回帰係数は、実測値と予測値との差ができるだけ小さくなるように求めます。具体的には、残差平方和が最小となるようにします。たとえば
y = a0 + a1 * x1 + a2 * x2
の回帰係数 a1, a2 は、次の連立方程式で求めます。
- S11 * a1 + S12 * a2 = Sy1
- S21 * a1 + S22 * a2 = Sy2
ここで、Sij は、i の偏差(平均との差)と j の偏差との積和です。
回帰係数が求まれば、a0 は
- a0 = average( y ) - a1 * average( x1 ) - a2 * average( x2 )
で求められます。
課題
課題1
インターネットで検索して、以下の問いに答えてください。
- 連立一次方程式の解法は、反復法と直接法に大別されます。その違いを説明してください。
- たくさんある反復法の中から2つ選び、その違いを説明してください。
- たくさんある直接法の中から2つ選び、その違いを説明してください。
課題2
(Sympy, Numpy.ligalg, Scipy.ligalg を使わない問題)
連立方程式1
3 x1 + 2 x2 + 7 x3 + x4 = 8
x1 + 5 x2 + x3 - x4 = 5
4 x1 + x2 + 3 x3 - 2 x4 = 7
x1 + 6 x2 + 4 x3 + 3 x4 = 13
連立方程式2
x1 + x2 + x3 + x4 + 5 x5 = 14
3 x1 + 2 x2 + 10 x3 + 4 x5 = 12
15 x1 + 2 x2 + 3 x3 + 4 x4 + 5 x5 = 20
x1 + 10 x2 + x3 + 3 x4 = 15
3 x2 + 5 x3 + 15 x4 + x5 = 10
連立方程式3
x2 + x3 + x4 = 5
x1 + x3 + x4 = 3
x1 + x2 + x4 = 6
x1 + x2 + x3 = 7
に対して、以下の2つの課題を解いてください。
-
反復法を使って連立方程式を解く Python プログラムをインターネットで検索し、それを使って(必要があれば適当に改変して)上記の連立方程式を3つとも解いてください。また、そのプログラムが記載してあったURLを明記し、たくさんある反復法のうち何法なのかも明記してください。ただし、Sympy, Numpy.ligalg, Scipy.ligalg を使わないプログラムを使うこと(Numpy, Scipyは使っても良い)。
-
直接法を使って連立方程式を解く Python プログラムをインターネットで検索し、それを使って(必要があれば適当に改変して)上記の連立方程式を3つとも解いてください。また、そのプログラムが記載してあったURLを明記し、たくさんある直接法のうち何法なのかも明記してください。ただし、Sympy, Numpy.ligalg, Scipy.ligalg を使わないプログラムを使うこと(Numpy, Scipyは使っても良い)。
課題3
(Sympy, Numpy, Scipy を使わない問題)
-
説明変数が2変数の場合に、1変数の影響を除いた偏回帰係数を算出する関数を作成してください。
-
また、その関数を用いて、家賃のデータ を使って、「徒歩(分)」「専有面積(㎡)」の2変数から「家賃(円)」を予測する線形重回帰モデルを、scikit-learn, sympy, numpy, scipy を使わずに作成してください。pandasは使って構いません。その後、scikit-learnを使った結果と比較してください。
課題4
(Sympy, Numpy.ligalg, Scipy.ligalg を使っても良い問題)
- 家賃のデータ を使って、「徒歩(分)」「専有面積(㎡)」「築年数(年)」「階数(階)」の4変数から「家賃(円)」を予測する線形重回帰モデルを、scikit-learnを使わずに作成してください。ただし、sympy, numpy, scipy, pandas は使っても構いません。その後、scikit-learnを使った結果と比較してください。