グラフ理論とは?
グラフ(Graph)1とは、点と辺によって構成される図形のことです。
例えば鉄道の路線図、Twitterのフォロー関係、コンピューターネットワークなどもグラフで表すことができます。
グラフ理論は、グラフに関する数学の理論のことです。
例えば、A駅からB駅までの経路検索といったシーンで、グラフ理論が応用されています。
「つながる。」とは?
「つながる。」は@YukiMihashiさんがScratchで製作されたパズルゲームで、第3回全国小中学生プログラミング大会のグランプリに選ばれた作品です。

タイルをクリックするとタイルが回転し、人と人が白い線によってつながるようにするゲームです。
「つながる。」はこちらで遊ぶことができます:
https://scratch.mit.edu/projects/180846317/
グラフ理論で「つながる。」のステージを解けるの?
GraphillionというPythonライブラリを使って「つながる。」のステージを解くことができます。
Graphillionには、2012年ごろに話題になった「お姉さん問題」を高速に解くことができるアルゴリズムが実装されています。
再生回数200万回突破!「『フカシギの数え方』おねえさんといっしょ!みんなで数えてみよう! 」 動画はこちら→ https://t.co/3XPmHVoSIe pic.twitter.com/yMECCqFX2w
— 日本科学未来館 (@miraikan) 2018年6月7日
Graphillionを利用するにはグラフ理論の用語を知っている必要がありますが、この記事では必要な用語が出てきたときに注釈を付けるようにしました。
「つながる。」のステージを解く
何が答えとなるのか?
ステージのタイルを回転させ、人と人を上手に結ぶことができれば、そのステージが解けたことになります。
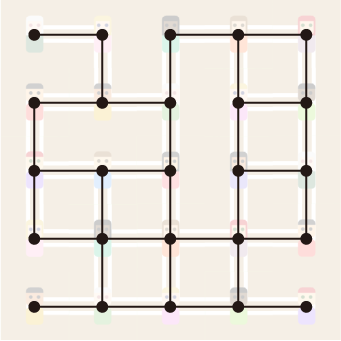
上手に結んだ人と人とのつながりはグラフであると言えます。
このグラフは必ずグリッドグラフ2の部分グラフ3となっています。
Graphillionが得意なこと
Graphillionはベースとなるグラフから条件を満たす部分グラフ3を高速に探し出すことが得意です。
「お姉さん問題」を例にしてみます。
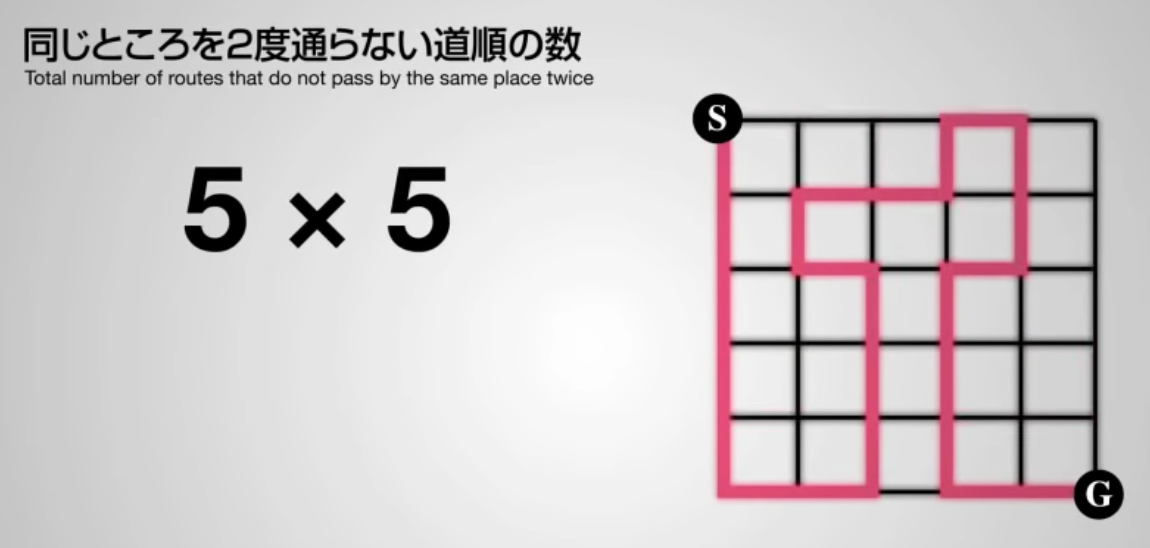
ベースはグリッドグラフ2で、条件は始点(S)から終点(G)までの道4とすれば、条件を満たす部分グラフは同じところを2度通らない道順だといえます。Graphillionを使えば条件を満たす部分グラフの数を数えたり、列挙することができます。
Graphillionで「つながる。」のステージを解く
「つながる。」のステージもGraphillionが得意な問題に置き換えてみましょう。
「つながる。」のステージを解くには、グリッドグラフ2をベースとし、タイルを回転してできる部分グラフをすべて探し出せば良さそうです。
ですが、タイルを回転してできるという条件をそのまま利用することはできません。Graphillionで問題を解くにはグラフ理論の言葉で表現されている必要があるからです。
グラフ理論の言葉で条件を考える
ステージのタイルをよく観察すると、タイルの種類ごとにタイルの上にいる人(以下、点と呼ぶ)の次数5が決まっていることがわかります。
| タイル |  |
 |
 |
 |
 |
|---|---|---|---|---|---|
| 次数 | 1 | 2 | 2 | 3 | 4 |
各点に次数の条件を付けることで、タイルを回転してできるという条件をうまくグラフ理論の言葉に置き換えできたかのように思えます。
しかし、点の次数が2と対応するタイルは2種類あり、次数の条件だけではタイルを区別できる条件とはなっていません。
L字タイルとI字タイル
点の次数が2と対応する2種類のタイルを、L字タイル、I字タイルと名付けて呼ぶことにします。
L字タイルとI字タイルの上にある点には次数2という条件に加え、もう少し条件を付けましょう。
I字タイルの上にある点の周りの辺は、下図のどちらかになっています。
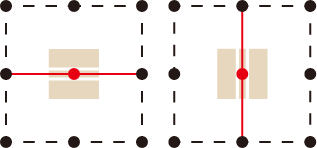
同様にL字タイルの上にある点の周りの辺は、下図のどれかになっています。
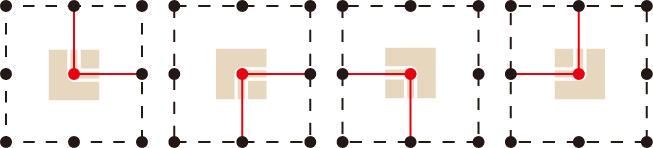
条件は上のもので正しいのですが、Graphillionでは「どれか」といったOR条件を付けるよりもAND条件を付ける方が簡単な都合上、L字タイル、I字タイルのお互いの条件を否定した条件を付けると良いです。
I字タイルの上にある点の周りの辺は、下図のどれにも当てはまらない
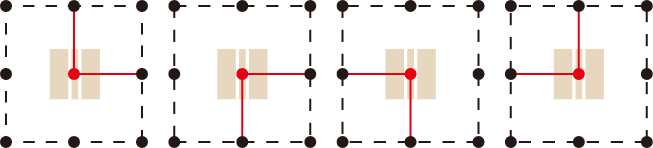
L字タイルの上にある点の周りの辺は、下図のどちらにも当てはまらない
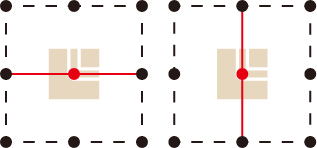
(Graphillionでは、excludingメソッドで「部分グラフとして含まない」という条件を設定できるので、2辺からなるグラフを部分グラフとして含まないように条件を設定します)
プログラムを書いてステージを解く
必要なライブラリと環境
- Python 2.7 or Python 3.7.2
graphillionnetworkxmatplotlib
Graphillion - 無数のグラフを効率的に扱うための高速・軽量ライブラリ に書いてあるの手順に従い、 networkx, matplotlib, graphillion を使える状態にしておきます。
(2019/03/21 追記)
Graphillion が Python 3系でも動くようになったので、Python 3.7.2 においても実行できるようにプログラムを修正しました。
macOSの場合、グラフをプロットするにはこちらの設定が必要かもしれません: matplotlib.pyplotをimportするとエラーが出たり画面が白く描画される問題の対応(macOS)
ステージを解くプログラム
実装方法については割愛しますが、実装の方針はすでに説明しており、Graphillion: 数え上げおねえさんを救え / Don't count naively
(YouTube動画)を見ればある程度実装方法がわかるかと思います。
ステージはタイルの並びなので、入力はタイルの並びとなります(tiles)。
# coding: UTF-8
from graphillion import GraphSet
import networkx as nx
import matplotlib.pylab as plt
import graphillion.tutorial as tl
(L, I) = ('TILE_L', 'TILE_I')
# tl.draw() のほぼコピペ(ラベルを表示する処理を追加)
def draw(g, universe=None):
if not isinstance(g, nx.Graph):
g = nx.Graph(list(g))
if universe is None:
universe = GraphSet.universe()
if not isinstance(universe, nx.Graph):
universe = nx.Graph(list(universe))
n = sorted(universe[1].keys())[1] - 1
m = universe.number_of_nodes() // n
g.add_nodes_from(universe.nodes())
pos = {}
for v in range(1, m * n + 1):
pos[v] = ((v - 1) % n, (m * n - v) // n)
nx.draw(g, pos)
nx.draw_networkx_labels(g, pos) # ラベルを付与
plt.show()
def get_degree(tile):
if tile == L or tile == I:
return 2
return tile
# ステージのサイズとタイルの並びをここに入力
# 1: 次数1に対応するタイル
# L: 次数2に対応するタイルでL字のもの
# I: 次数2に対応するタイルでI字のもの
# 3: 次数3に対応するタイル
# 4: 次数4に対応するタイル
n = 9
tiles = [ L, 3, 3, 3, 3, 3, 3, 3, L,
3, 4, L, L, L, L, L, L, 3,
3, 3, I, I, I, I, I, 3, 3,
3, L, L, I, L, 1, L, L, 3,
3, L, 3, L, L, L, I, L, 3,
3, L, 3, 3, L, 3, 3, L, 3,
3, 3, 3, 1, L, L, I, L, 3,
3, 3, 3, 3, 3, 3, 3, 3, 3,
L, 3, 3, 3, 3, 3, 3, 3, L, ]
# n*nのグリッドグラフの生成
# draw(grid_graph) で点と辺の位置関係を確認してみてください
grid_graph = tl.grid(n - 1, n - 1)
# ベースのグラフ(grid_graph)をセット
GraphSet.set_universe(grid_graph)
# grid_graphの点のラベルが 1,2,3,...,n*n なのでインデックスをずらす
tiles.insert(0, None)
# 次数条件
degree_constraints = {v: get_degree(tiles[v]) for v in range(1, n * n + 1)}
# 各点に次数条件を付けたグラフセット
graphs = GraphSet.graphs(degree_constraints=degree_constraints)
# I字タイルとL字タイルの上の点には追加の条件を付ける
for v in range(1, n * n + 1):
if tiles[v] == L:
if (v - 1, v) in grid_graph and (v, v + 1) in grid_graph:
graphs = graphs.excluding([(v - 1, v), (v, v + 1)])
if (v - n, v) in grid_graph and (v, v + n) in grid_graph:
graphs = graphs.excluding([(v - n, v), (v, v + n)])
if tiles[v] == I:
if (v, v + 1) in grid_graph and (v, v + n) in grid_graph:
graphs = graphs.excluding([(v, v + 1), (v, v + n)])
if (v, v + n) in grid_graph and (v - 1, v) in grid_graph:
graphs = graphs.excluding([(v, v + n), (v - 1, v)])
if (v - 1, v) in grid_graph and (v - n, v) in grid_graph:
graphs = graphs.excluding([(v - 1, v), (v - n, v)])
if (v - n, v) in grid_graph and (v, v + 1) in grid_graph:
graphs = graphs.excluding([(v - n, v), (v, v + 1)])
print('ステージの解:{}通り'.format(graphs.len()))
for g in graphs:
draw(g)
プログラムを実行
上のコードにある n と tiles は「つながる。」の「世界のステージ9」に対応しています。

Pythonでプログラムを実行すると、 ステージの解:3通り と表示され、3通りの答えが表示されます。

このグラフを見ながらタイルを回転させればステージをクリアできるはずなのですが、「つながる。」では3通りの答えすべてがクリアとならず、3通りの答えのうちひとつだけがクリア扱いとなるようでした。
(ステージの製作者が意図した解答のみがクリア扱いとなります)
すべての人がつながっている必要はなかった
「つながる。」というタイトルから、すべての人がひとつにつながっていないといけない気がするものですが、連結グラフ6であることがクリア条件ではありませんでした(例: 世界のステージ10)。
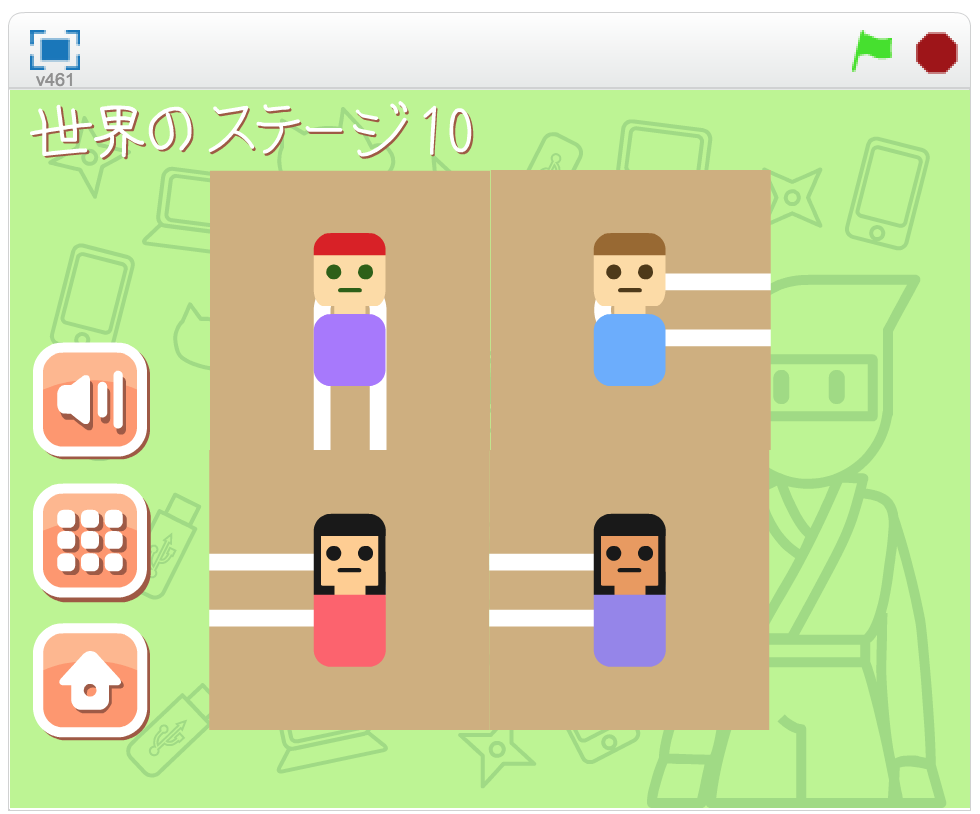
この仕様をうまく利用すると2通りの答えがあるステージで、片方は連結グラフ6でもう一方は非連結グラフ7とすることができ、非連結な方でクリアになるトリッキーなステージを作ることができます8。
つながっていない方がクリアになる「つながる。」ステージの例 pic.twitter.com/iitgDKrhog
— mascii (@mascii_k) 2018年10月24日
Graphillion(とNetworkX)を使えばこのようなステージも探し出すことができます。
まとめ
- Graphillionを使えば、「お姉さん問題」や「つながる。」といったグラフの組み合わせ問題が解けることは大変素晴らしいことです。
- 「つながる。」はScratchで作られていますが、ここまでのものを作れることを知りませんでした。
- Graphillionの記事が少ない中、「つながる。」という事例としてぴったりなパズルを題材に記事を書くことができて良かったです。読者の方々にグラフ理論とプログラミングの面白さが伝わりましたら幸いです。