はじめに
本資料はMySQLでのインデックス勉強会に用いる資料です。
記事としては冗長ではありますが、あくまで勉強会の資料ですのでご了承ください。
資料の公開場所としてQiitaがちょうどよかったので選択しました。
Relational Database
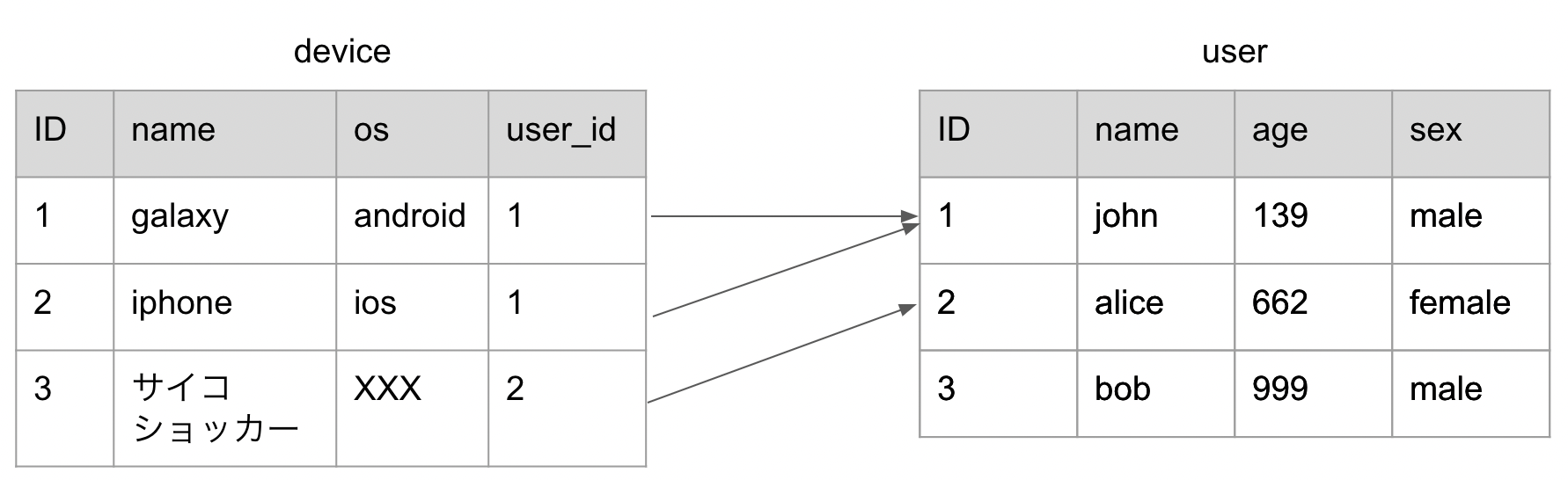
1行を1レコードとするテーブル形式で表します。
主キーでそのテーブルを代表するカラムを指定し、外部キーで別テーブルと関連付けます。
テーブルの設計には正規化と呼ばれる設計手法があり、これでデータの重複をなるべく無くして整合的にデータを取り扱えるようにすることを目指します。
インデックス
索引とも呼びます。データへのアクセスを少ない実行数にして高速化するために作成します。
本の末尾などに単語をあいうえお順、アルファベット順にまとめた索引がついているのを目にするかと思います。
特定のルールに従って並べられているから調べたい単語を探すにも最初から順に見ていく必要はなく、一気に特定の文字クラスタまで飛んでから探せますよね。
データベースでもこういうのが作れます。
いくらコンピュータは人と比べて処理速度が早いと言っても無駄は省いてより早い時間で取得したいですから。
下記のユーザーテーブルを例に取ります。
| id | name | age | sex |
|---|---|---|---|
| 1 | jonh | 139 | male |
| 2 | alice | 662 | female |
| 3 | bob | 999 | male |
レコードの格納位置、格納メモリがID順で連番になっていればIDでの検索をしたければ二分探索をすれば速いですし、名前であれば辞書順に並べられていれば探索を効率化できます。
性別を男女で完全に分割して、その上で年齢順にすれば特定の性別の中での特定の年齢の人を探しやすくなるでしょう。
とはいえ、データベースにおいてはIDのみでしか検索しない、名前のみでしか検索しないといった、特定条件でのみしか検索しないなんてことはないですよね。
そのために、レコードの実態とは別にインデックスを作成し、本の索引のようにインデックスには検索するための対象カラムとレコードの実態をさす格納位置を持ちます。
突っ込まれそうなので補足するとクラスタインデックスに実態を持たせる場合もありますが、今回は説明が面倒なので考慮しません。
ではこのインデックスはどのようにつくられるのでしょうか？
木構造
B木、B+木と呼ばれるデータ構造で作成されます。
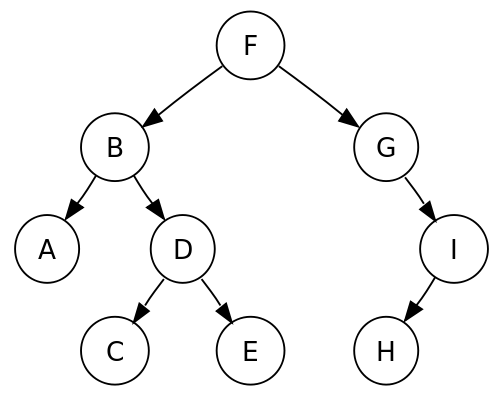
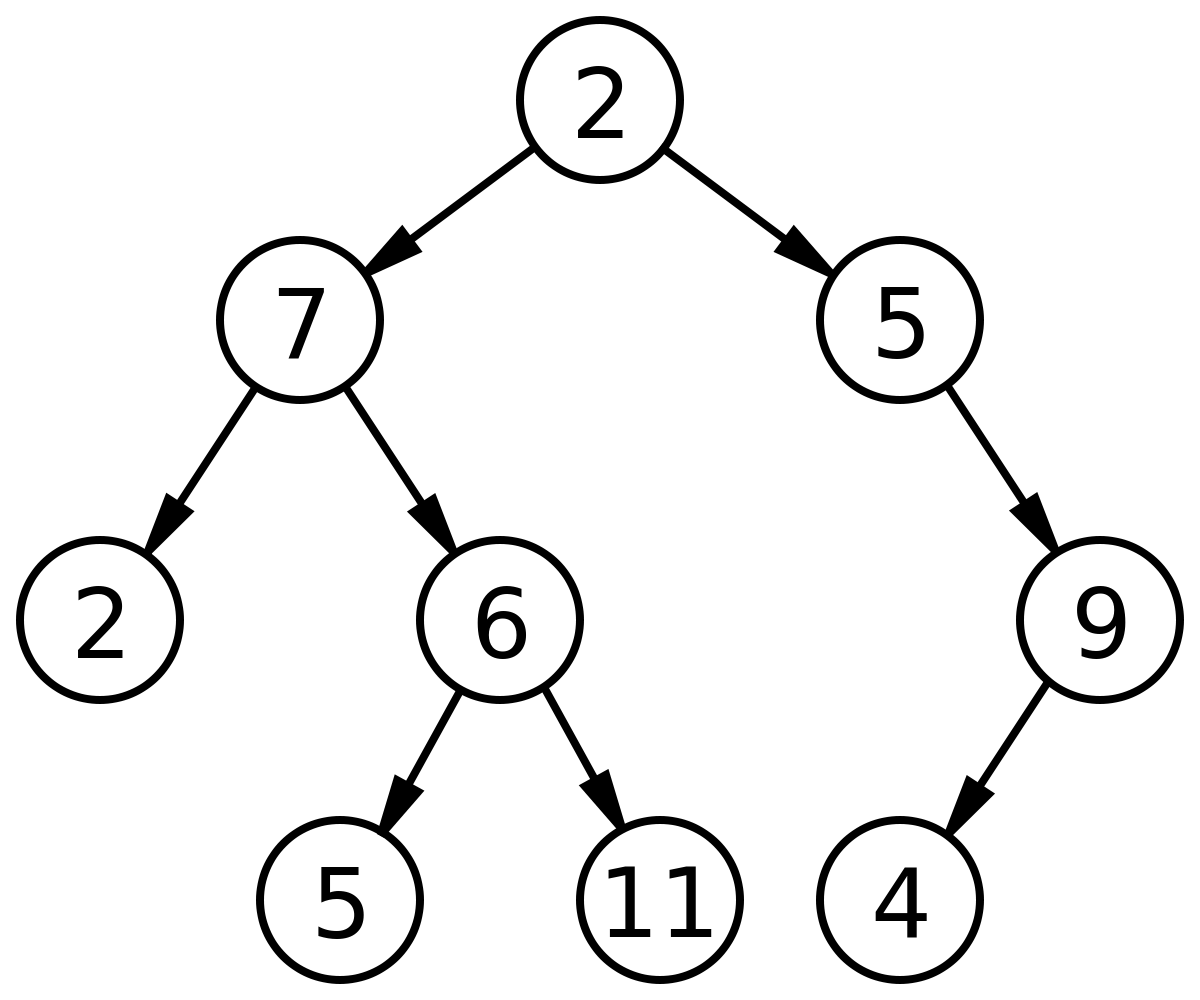
これらは木構造の一種で、そもそも木構造とは下記画像のようなトーナメント形式のグラフを指します。
木構造にはノードとエッジの2つの概念が存在し、ノードが丸の部分、エッジが丸をつなぐ線の部分を指します。
頂点のノード(下記画像ではF)をルートノードと呼び、根とも言います。
そして、その下に繋がるノードを、子ノード孫ノードと呼びます。
逆にノードの上に繋がるノードを親ノードと呼び、繋がり先を親子関係で表現します。
末代のノード(ここではA, C, E, H)をリーフノード、または葉と呼びます。
根っこがあって枝(エッジ)があって先端に葉があって。まさに木ですよね。
下記は有向グラフと呼ばれるエッジが向きを持つグラフですが、向きを持たない無向グラフもあります。
さて、これを踏まえた上でB木を見ていきます。
B木
多分木のバランス木です。
B木のBはバランスのBです。バイナリーではありません。
そうは言っても何言ってんだとなるかと思うので、ぽんち絵を作成しました。
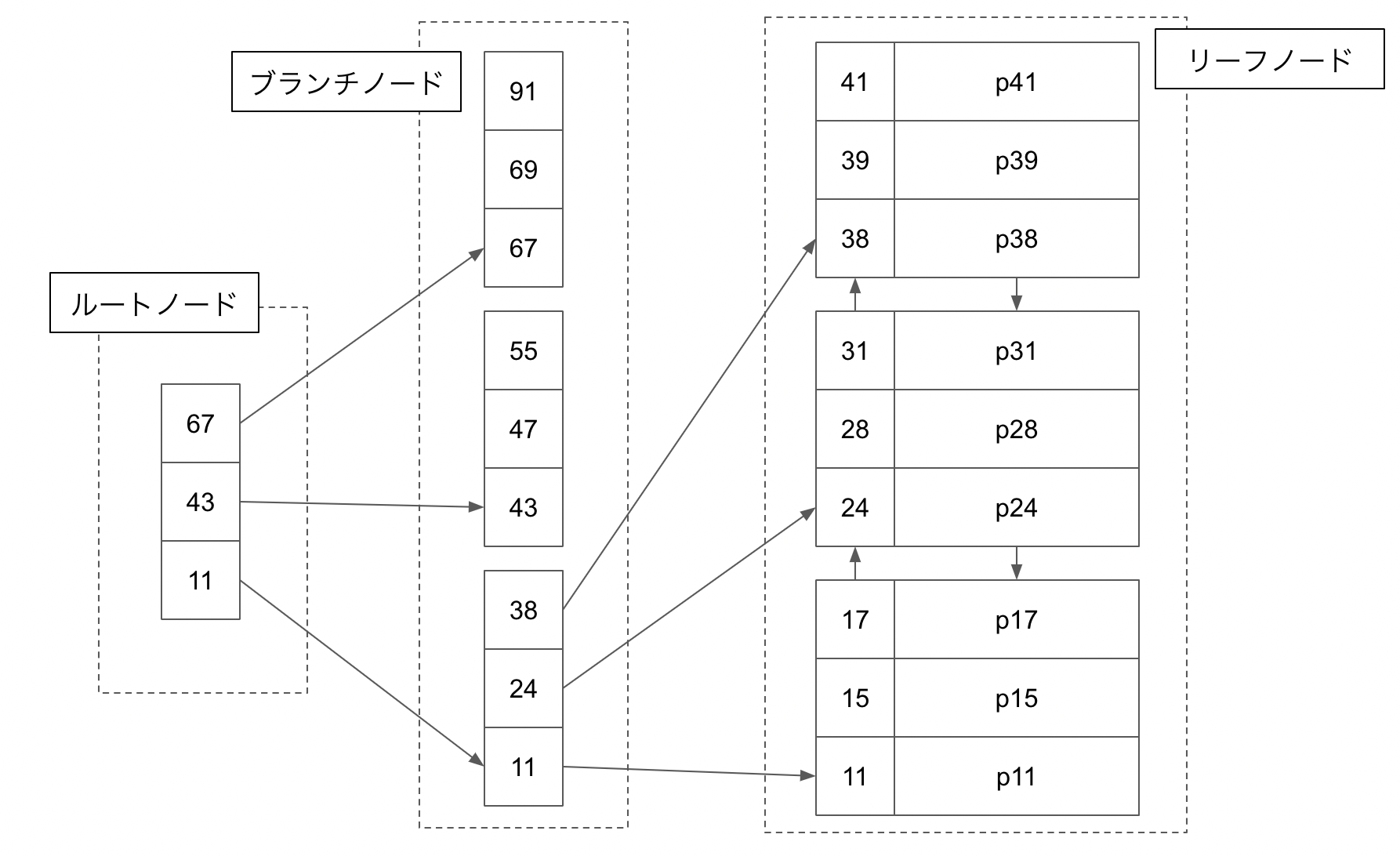
※下記図はB+木ですが、SQLパフォーマンス詳解に合わせてB木と呼びます。
ルートノードがあり、ブランチノードという間に挟むノードがあり、レコードの実態への参照を持つリーフノードが存在します。リーフノードの右側にある p** がレコードの実態への参照を示しているものとしてみてください。
リーフノードは隣り合うリーフノードへの双方向エッジを持っています。
私の作成したぽんち絵は、エッジの繋がる先は最小値を指します。
しかしなぜB木が採用されるのでしょうか？
B木の利点
まず、木構造を用いない場合を考えます。
インデックスの章でも述べた通り、上から順に総舐めしていくのは効率が悪いと言わざるを得ません。
もちろん、レコード数が少なかったり、例えばデータの順序がID順で調べたいIDが若いものだったら上から見ていくほうが速いでしょう。
しかし、数が多くてIDが大きい数だったら？ 名前で見たかったら？
そうなると索引が欲しくなりますよね。
| id | name | age | sex |
|---|---|---|---|
| 1 | jonh | 139 | male |
| 2 | alice | 662 | female |
| 3 | bob | 999 | male |
次に平衡木(バランス木)でない場合を考えます。
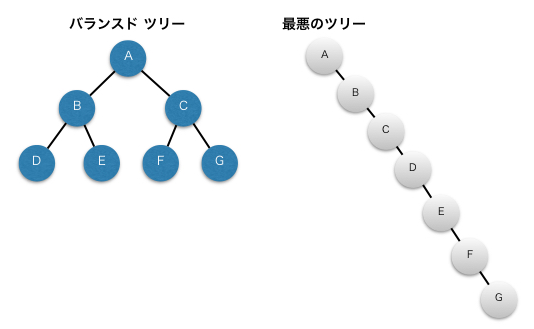
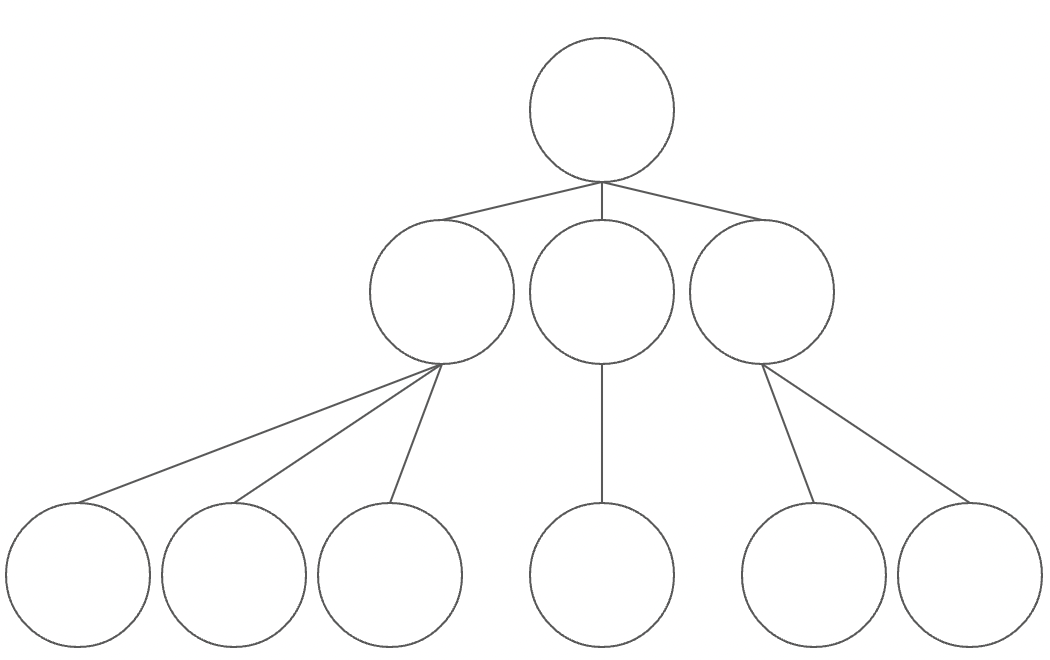
まず平衡木とは、根ノードから子を持たない末端の葉ノードまでの深さ（高さ）がなるべく等しくなるように構築されたものを指します。
下記図がわかりやすいですね。
最悪のツリーでは上から総舐めするのと変わりません。
2つを見比べたとき探索するならバランス木ですよね。
そして2分木ではなく多分木である理由です。
N分木というのは一つのノードがいくつまで枝分かれできるかを指します。
2分木
3分木
多分木の利点として、N分木のNの分だけ木の深さを浅くできます。
木の深さはこのNをlogの底とし、Xをデータ量として $O(log_NX)$ になります。
詳しい計算は私ができないので載せませんが、木が深くなると一つ一つのノードでの処理は簡単に済みますが深掘っていく過程で計算量が嵩むので、大量のデータを扱うデータベースではなるべく浅くしたいのです。
コラム: 対数
対数というのはある数Xを数Bのべき乗 $X = B^P$ として表した時のべき指数Pを指します。(wikipedia対数)
例えば $log_{10}100 = log_{10}10^2 = 2$ となります。
この例はピッタリ整数になりますが、平方数などのキリの良い数でなければ小数点が出そうです。
しかし、切り捨てを行ったときに見えてくるものもあります。
$log_{10}100 = 2$
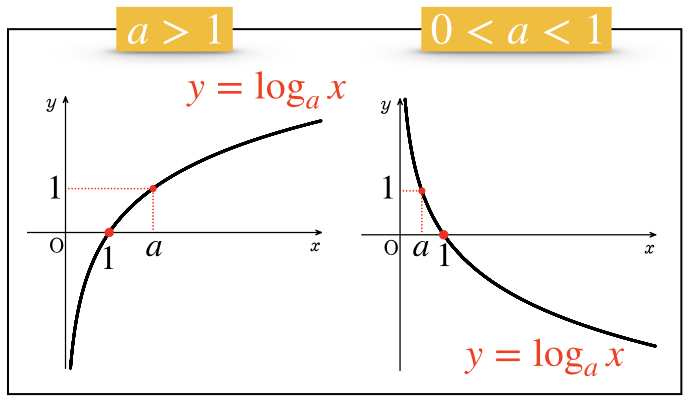
底Nの進数でみたときのNの桁数として見ることもできます。
このようなグラフになるのも納得ですね。
レコード数Xが大きくなるほど $O(log_NX)$ の真価が発揮され、100万(1000000)レコードあってもインデックスを用いての探索ならば、底が10のとき100万レコードの桁数 "1000000".length = 7 回でアクセスできます。
すごいッスネ！
インデックス
クラスタインデックス
ここからはDBのインデックスについて深堀っていきます。
MySQLで見ていきます。
主キー(またはユニークキー)で作成されるインデックスです。
B木の章でリーフノードがレコードの実態への参照を持つと話しましたが、クラスタインデックスがそれに当たります。
なので他比べてインデックスサイズが大きいです。
もう一つ、セカンダリインデックスというインデックスもありますが、こちらは持ちません。これは後述します。
ユニークキーが使われる場合は主キーが存在しない場合です。
MySQLのクラスタインデックスについては下記が詳しいです。
また、クラスタインデックスはデータが並び替えられて保存されています。
InnoDB ストレージエンジンによって、テーブルデータが、主キーカラムに基づいて、超高速ルックアップおよびソートを実行するように物理的に編成されます。
なのでソートや範囲検索に用いるのに適しています。
SQLだと複数行取ってくることが往々にあります。
キャッシュには空間的局所性という連続してアクセスされるデータは隣接したアドレス空間に存在している可能性が高いことを利用した性質があり、その性質から考えても理にかなっていますね。
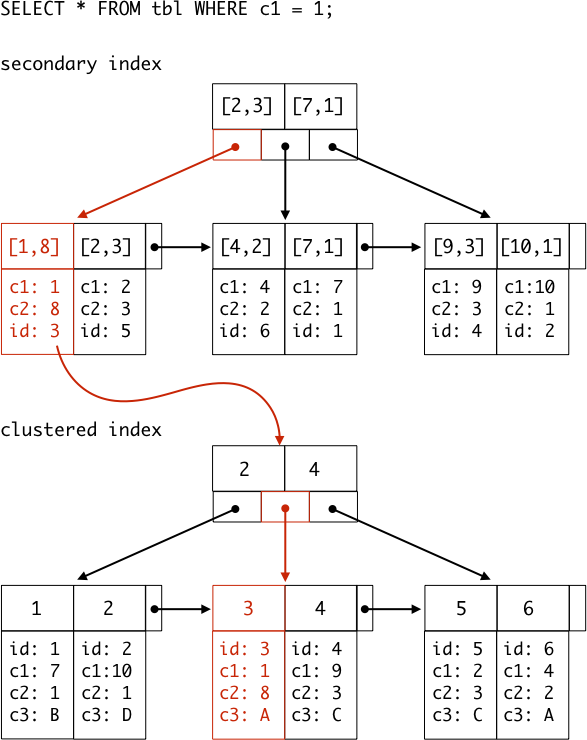
セカンダリインデックス
クラスタインデックスでないインデックスです。そのまんまですが、非クラスタインデックスとも言われます。
セカンダリインデックスは上記の通り、リーフノードがレコードの実態への参照を持ちません。
代わりに、クラスタインデックスのキー値を持ちます。
ですので、一度セカンダリインデックスを通ってから、クラスタインデックスへといくため2つのインデックスを舐めることになります。
クエリやテーブル構造によりますが、N+1にならないのであればクラスタインデックス(=id)のみを取得するクエリと本クエリを分けて、前クエリで取得したidを元にIN句などで検索をかけていく方が速い場合もあります。
とはいえ往々にクエリを複数流す方が時間がかかるので、手段の一つとして記憶の片隅に入れておくのがいいかと思います。
しかしなぜセカンダリインデックスにもレコードへの直接参照を持たないのでしょうか？
それは、レコードの参照がずれる可能性があるためです。
どういうことかと言いますと、先ほどクラスタインデックスは参照性を高めるために物理的に編成していると述べました。
登録、更新、削除など、データを変更する処理が走った時に再編成が入ります。
そうなると参照先が変わります。
参照先が変わるということはクラスタインデックスに入れているポインタを変えなければいけませんよね？
セカンダリインデックスもそのポインタを持つとなると、参照先変更の影響範囲が広くなってしまいます。
ただでさえインデックス自体の作り直しも入るので変更処理が重たくなります。
インデックスの作りすぎはよくないって言われるのも理解できます。
snowflakeなどのDWHには変更処理のコストを上げる代わりに取得処理を高速化しているものもあります。
こちらの内部処理はよく知らないので、名前を挙げる程度にします。
複合キーのインデックス
複合キーとは、複数のカラムを組み合わせたインデックスのことを指します。
複数の要素で一意に特定できるようなレコードで複合ユニークキーのように用います。
下記テーブルでの社員コードの所属コードの複合インデックスの場合を考えます。
| 社員コード | 所属コード | 社員名 |
|---|---|---|
| 1001 | 101 | テスト太郎D |
| 1003 | 101 | テスト太郎C |
| 1004 | 101 | テスト太郎A |
| 1002 | 102 | テスト太郎B |
| 1005 | 102 | テスト太郎 |
テーブル設計の欠陥みたいな例になってしまいますが、何らかの事情で所属コード内で社員コードが一意だったとします。
そのとき、インデックスは下記クエリで作成するのですが、複合インデックスでは順番が重要になります。
create unique index employees_pk on emplotees (社員コード, 所属コード)
複合インデックスでは、一つ目のインデックスをまず見て、重複があったときに二つ目のインデックスを見ます。
上記の例では社員コードを見てから所属コードを見ます。
なので、社員コードのインデックスは無条件で効きますが、所属コードのみだとインデックスが効きません。
インデックスが効かなくなる場合
2つ例を挙げます。
LIKE %**%
対象カラムに対して一致検索をかけるLIKE句というものがあります。
下記のように使用することで、完全一致検索になります。
select 列名 from テーブル名 where 列名 like '検索文字';
ワイルドカードを用いることもできます。
| ワイルドカード文字 | 意味 |
|---|---|
| % | 0文字以上の任意の文字列 |
| _ | 任意の1文字 |
ではLIKE句でインデックスが効かなくなる場合はどんなときでしょうか？
それは ワイルドカードから始まる検索です。
下記のような場合ですね。
select 列名 from テーブル名 where 列名 like '%XXX';
逆に後にワイルドカードがくる場合はインデックスが効きます。
select 列名 from テーブル名 where 列名 like 'XXX%';
参考: インデックスが使えない検索条件
CTE句, サブクエリ
CTE句やサブクエリでのインデックスカラム取得の場合はインデックスが効かなくなる場合があります。
現在はDB側がいい感じに解釈してくれてインデックスを再付与してくれますが、再度インデックスを付け直す処理が入ってしまいます。
コラム: サブクエリ
サブクエリとは下記のようにクエリ内に存在するクエリを指します。
select
id
from
emproyees
where
office_id in (
select
id
from
office
where
locate like '%東京%'
)
コラム: CTE句
上記サブクエリのような処理は複数箇所で使われる場合があります。
すると共通化したくなりますよね。
それを実現します。
with office_locate_id as (
select
id
from
office
where
locate like '%東京%'
)
select
id
from
emproyees
where
office_id in office_locate_id
上記のように上に切り出せますし、複数箇所で使われているならキャッシュが効いたり、何度の問い合わせが走ったりがなくなります。
発展
ハッシュインデックス
インデックスの作られ方はB木だけではありません。
発展として、B木以外のインデックスの作られ方の一つであるハッシュインデックスを挙げます。
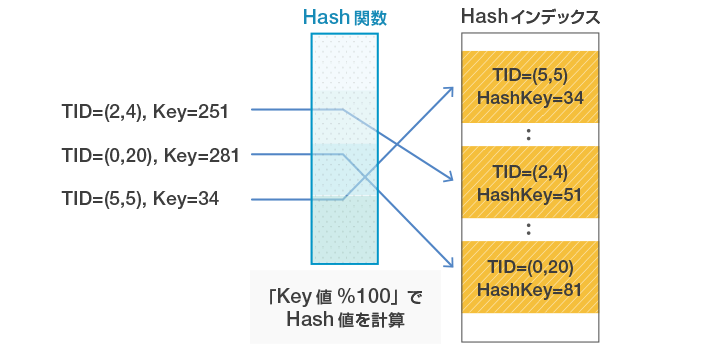
ハッシュ関数と呼ばれる、値を突っ込むと特定の値を返してくれる関数を通して該当メモリを返却してくれるインデックスです。
下記図が参考になります。
というかこれもう普通にハッシュテーブルですね。
B木インデックスと比べて、うまくハッシュ値がばらければ、根っこから見ていかなければならないB木インデックスと異なりO(1)で検索が可能ですが、一致検索しかできないので範囲検索や部分一致検索には向いていません。
ビットマップインデックス
発展の2つ目としてビットマップインデックスを挙げます。
下記データの血液型に対して
| id | name | age | blood_type |
|---|---|---|---|
| 1 | jonh | 139 | A |
| 2 | alice | 662 | B |
| 3 | james | 32 | O |
| 4 | bob | 999 | AB |
ビットマップとして用意するとこんな感じ。
| blood_type | 1 | 2 | 3 |
|---|---|---|---|
| A | 0 | 0 | 1 |
| B | 0 | 1 | 0 |
| O | 1 | 0 | 0 |
| AB | 0 | 1 | 1 |
ビットの配置を見て、対象レコードを絞り込みます。
ビットは $2^N$ で増えていくので、カーディナリティが低いカラムに対して有効になります。
B木だと性質上OR検索ではほとんどの場合インデックスは使用されないのですが、ビットマップインデックスならOR検索でもインデックスが使用されます。
おわりに
インデックスについて全体的に舐めました。
かなり冗長になってしまいましたがお許しください。
本当ならinnoDBやMyISAMといったエンジンについてや、JOINのインデックスの使われ方なども触れた方がより濃い内容にはできたのですが、今回はここまでと致します。
読んで頂きありがとうございました。