はじめに
固定小数点と浮動小数点について、まとめる機会があったので記事として残そうと思う。
固定小数点
ビット列のどこに小数点があるか、あらかじめ決めてしまい表現する。
メリット
- 整数で処理できる(計算コストが低い)
デメリット
- 扱える値の範囲が狭い
どういうことか、以下の例に沿ってみていく。
例
10進数
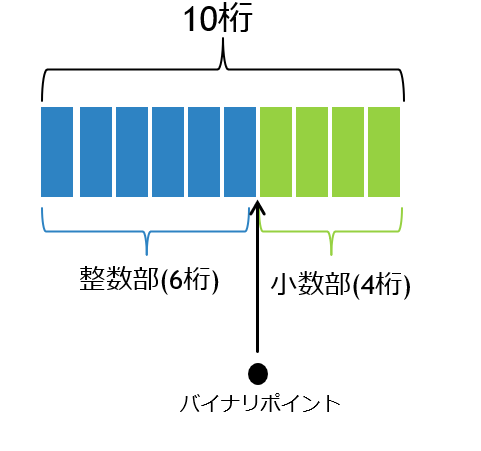
上のイメージのように、10桁の数
$$1234567809$$
を考えると
となる。これは、
のように、それぞれの桁に重みを与えてやると
1 \times 10^5 + 2 \times 10^4 + …… 5 \times 10^1 + 6 \times 10^0 +\\
7 \times 10^{-1} + 8 \times 10^{-2} + …… + 9 \times 10^{-4}\\
=123456.7809
といったように、それぞれの桁の数に対応した重みを掛け合わせることで表現できる。
これと同じことを2進数で行う。
2進数
上のイメージのように10bitの数
$$(0110101111)_2$$
を
と考えると、
$$+(26.9375)_{10}$$
となる。これも、
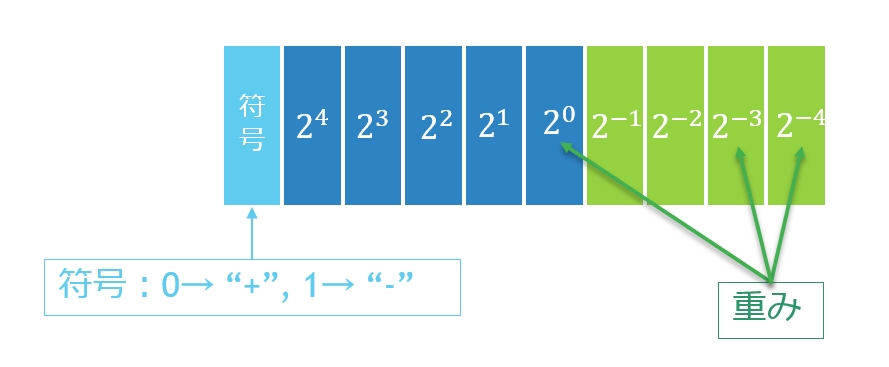
のように桁に重みを与えてやることで、
(-1)^0 \times (1 \times 2^4 + 1 \times 2^3 + …… 0 \times 2^1 + 1 \times 2^0 +\\
1 \times 2^{-1} + 1 \times 2^{-2} + …… + 1 \times 2^{-4})\\
=+26.9375
となる。
これらから、どこに小数点を持つか分かってさえいれば値を整数で処理できるが、扱える値の範囲が狭いことが分かる。
以上のように、ビット列のどこに小数点があるか、あらかじめ決めてしまい表現する方式を固定小数点という。
また、以下のように小数点を一番右に持ってくることで整数を表せる。
固定小数点を計算するコード
bit列を配列で保持
# include <iostream>
using namespace std;
const int bitNum = 10; // bit数
const int binary_point = 5; // 小数点位置(整数部数)
int main() {
int bit[bitNum+1] = {0, // 符号部
1, 1, 0, 1, 0, // 整数部
1, 1, 1, 1 // 小数部
};
double res = 0;
int isminus = bit[0] == 1 ? -1 : 1; // 符号の確認
double weight = (1 << (binary_point-1)); // 重みの最大値 2^(整数部分-1)
for(int i = 1; i < bitNum; i++) { // bit[0]は符号だから1から始める
res += weight * bit[i];
weight /= 2.0;
}
cout << res * isminus << endl;
return 0;
}
bit列を2進数リテラルで保持
# include <iostream>
using namespace std;
const int bitNum = 10; // bit数
const int binary_point = 5; // 小数点位置(整数部数)
int main() {
int bits = 0b0110101111; // bit列
int bitmask = (1 << (bitNum - 1)); // bitmask (0b1000000000)
double res = 0;
int isminus = (bits & bitmask) == 0 ? 1 : -1; // 符号の確認
bitmask = (bitmask >> 1); // 見る桁を1桁右にずらす
double weight = (1 << (binary_point-1)); // 重みの最大値 2^(整数部分-1)
for(int i = 1; i < bitNum; i++) { // bit[0]は符号だから1から始める
if((bits & bitmask) != 0) res += weight;
weight /= 2.0;
bitmask = (bitmask >> 1); // 見る桁を1桁右にずらす
}
cout << res * isminus << endl;
return 0;
}
浮動小数点
- 指数形式で値を表現
- IEEE754規格で決まっている
- 浮動小数点にはいくつか種類があり、昔は処理の仕方がコンピュータによって違っていたらしく、それではいけないと規格が出来上がった
メリット
- 非常に大きな値から非常に小さな値まで扱うことが出来る
デメリット
- 計算が近似値計算なので誤差が発生する
非常に大きな値から非常に小さな値まで扱うことが出来る？
扱える範囲を10進数の指数形式で以下に示す。
単精度(32bit)
最小の正の数：$1.175494351e^{-38}$
最大の正の数：$3.402823466e^{+38}$
倍精度(64bit)
最小の正の数：$2.2250738585072014e^{-308}$
最大の正の数：$1.7976931348623158e^{+308}$
以上から指数表現を用いることで非常に大きな値から非常に小さな値まで表現を実現できていることが分かる。
指数形式で値を表現
上記で出てきた、「指数形式」について示していく。
例えば、10進数だと
$$3,000,000,000 = 3 \times 10^9$$
これを指数表現といい、2進数でも同じようにやる。
$$(110110100100000000000000000000000)_2 = (1.101101001)_2 \times 2^{32}$$
以降、指数形式において、
$$仮数 \times 基数 ^ {指数}$$
と表現する。
IEEE754に準拠した浮動小数点表現
上記で出てきた、「単精度」及び「倍精度」について、図で示す。
-
単精度形式：float型(32bit)
-
倍精度形式：double型(64bit)
以降、単精度を例に進めていく。
表現方法
正規化
最上位桁が0以外になるよう桁を合わせる操作。
指数部
指数部で2の補数表現を使わない理由として、$ \pm 0$ と、 $ \pm ∞$ を表すためというのが挙げられる。
指数部の表現
| 2進数 | 10進数 |
|---|---|
| 11111110 | 127 |
| : | : |
| 10000000 | 1 |
| 01111111 | 0 |
| 01111110 | -1 |
| : | : |
| 00000010 | -125 |
| 00000001 | -126 |
特別な場合
| 2進数 | 10進数 |
|---|---|
| 11111111 | ∞ |
| 00000000 | 0.0 |
0の表現
以上より、+0と-0が存在する。
誤差
ここからは、浮動小数点のデメリットとして挙げた近似値計算による誤差について、3つみていく。
丸め誤差
最下位桁より小さい部分について、四捨五入や切り捨て、切り上げが行われることにより発生する誤差
例として、小数点以下5桁までしか表せないときの $(0.1)_{10}$ の2進数で示す。
切り捨てられた場合、 $(0.00011)_2$ となり、
0 \times 2^{-1} + 0 \times 2^{-2} + 0 \times 2^{-3} + 1 \times 2^{-4} + 1 \times 2^{-5} = 0.09375
0.1にならず、誤差が発生していることが分かる。
情報落ち
指数部の値が異なる2つの数値の加減算において、指数部の小さな数値が指数部の大きな数値に合わされてから演算される。そのとき、指数部の小さいほうの仮数部の値が右シフトされて計算結果に反映されないために発生する誤差
例：
桁落ち
絶対値のほぼ等しい2つの数の差を求めたとき、有効桁数が大きく減るために発生する誤差
例：
まとめ
これらから、指数表現によって非常に大きな値から非常に小さな値まで扱うことが出来ることと近似値計算による誤差の発生について分かった。
以上のように、指数形式で値を表現する方式を浮動小数点という。