固定小数点と浮動小数点の求め方について備忘録代わりに簡単に書いておく。
詳しい内容が知りたい場合は適宜調べてください。
固定小数点
- 固定小数点は整数型を小数として扱う事が出来る
- 小数を固定する位置は__ソフト(ハード)の実装__によって決まる。
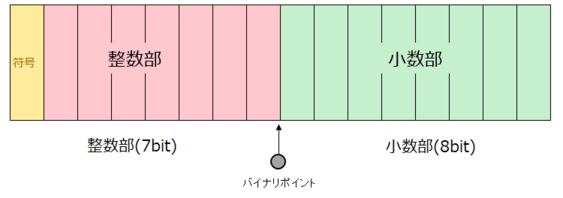
つまり、16bitの場合こう表現することもできるし
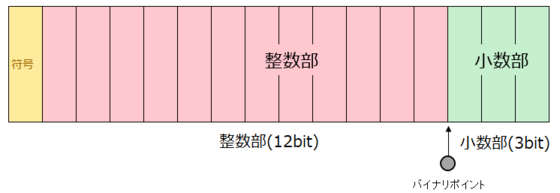
このように表現することも可能。
固定小数の構造
2 進数の場合、小数では桁が下がるにつれ 0.5 の乗数 ( 2 のマイナス乗) を表します。
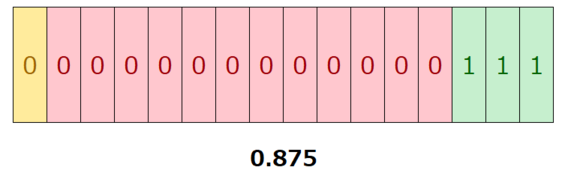
例では0.9の表現を求めてみる。
10進数の小数を二進数に変換するには小数部分に2を掛けて行き1.0になるまで繰り返せば良いです。
1.0を超えたら1を引いた値に2を掛けていく。
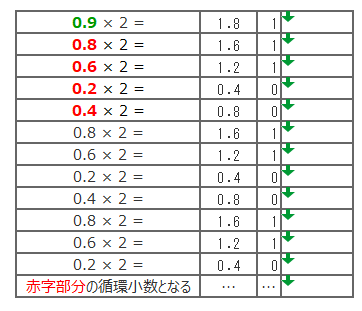
上から順に左→右に埋めていけばよい
小数部8bitなら0.8984375となります
小数部3bitなら0.875となります
結論：表現できるbit数が少ないと誤差が大きくなる。
浮動小数
IEEE754 という方式に準拠した 半精度浮動小数点(16bit)について書いてみます。
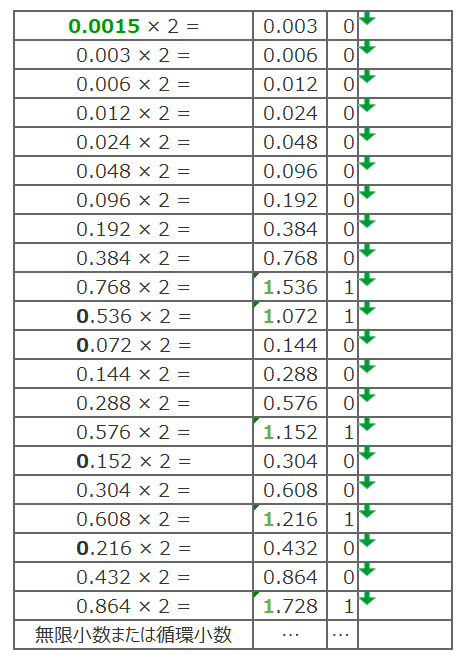
今回は0.0015を二進数の半精度浮動小数点(16bit)で表現してみたいと思います。
手順は以下の通りです。
- 仮数部の値を求める(やり方は固定小数と同じ)
- 1.xの形にする
- 1を外した値を仮数部として扱う
- 2の時に移動した数をバイアス値(16bitなら15)に足した値を指数部として扱う
以上。
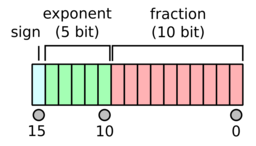
浮動小数点の構造
半浮動の浮動小数点では 16 ビットを以下のように 3 つに分割します。
仮数部の求め方
まず最初に仮数部を二進数で求めます(仮数部の求め方は固定小数の時と同じです）
色んな数を計算してみる分かると思いますが1.0で収束する事の方が稀です。
結果はこうなります。
00000000011000100100 …(以下省略)
次に小数点の位置をずらし1.xの形にします(小数点を右に10個分移動させます)
1.1000100100 …(以下省略)
最初の1を除いた先頭10bitの値が仮数部になります
1000100100
指数部の求め方
仮数部を1.xの形にする際に小数点を右に10個分移動させたので
指数は2E-10なのでバイアス値から-10します。
16bitは15なので、二進数にすると 01111ここから1010を引きます。
結果、指数は00101になります。
0 00101 1000100100
↑が半精度浮動小数で表した時の0.0015になります。
参考
https://www.macnica.co.jp/business/semiconductor/articles/intel/133327/