Pythonをやってたらコードがどんどん数学に見えてきたので、、数学とか統計とかを整理してみた

Pythonを勉強してたら、どうもコードが数学っていうか数式に見えてきたので、Pythonと数学ってとても親和性が高いなーって思った例を書いてみます。きがついたら統計まわりの話がほとんどです。。

この書籍「Pythonで理解する統計解析の基礎」ですが、Pythonをつかう際にめちゃくちゃ参考にさせてもらってます。筆者のかたありがとうございます。

確率分布と確率質量関数(確率密度関数)

さきほどの書籍に出てくる例で、出目の確率が異なるイカサマサイコロの例があります。
1〜6の目が出る確率が、

出目	1	2	3	4	5	6
確率	$\frac{1}{21}$	$\frac{2}{21}$	$\frac{3}{21}$	$\frac{4}{21}$	$\frac{5}{21}$	$\frac{6}{21}$

って偏りがあるサイコロの確率変数って話なんですがPythonをつかって、

import numpy as np

def F():
    _x_set = np.array([1, 2, 3, 4, 5, 6])

    def _f(x):
        if x in _x_set:
            return x / np.sum(_x_set)
        else:
            return 0
    return _x_set, _f # _x_setは取り得る値の集合、_fは確率質量関数

っていう確率変数を定義したとき、

X = F()
x_set, f = X

# 確率質量関数に値を代入して、確率のリストを作成
prob = np.array([f(x_i) for x_i in x_set])
print(dict(zip(x_set, prob)))

結果:
{
 1: 0.047619047619047616, 2: 0.09523809523809523, 
 3: 0.14285714285714285, 4: 0.19047619047619047, 
 5: 0.23809523809523808, 6: 0.2857142857142857
}

ってやって確率の配列を生成することが出来たり、

trial_count = 1000
sample = np.random.choice(x_set, trial_count, p=prob)  # サイコロをふる試行を、trial_count 回やった結果を取得。
print(sample)

結果:
[5 4 6 6 2 2 1 5 4 6 4 6 4 6 4 5 6 4 2 5 2 2 5 3 6 6 5 6 1 4]  #← 30回試行の例

というように、ある確率変数を1000回試行した結果を得ることができたりします。
確率変数の試行とか、ステキですね。。

さてココででてくる確率変数を返す関数の定義、別の例でたとえば二項分布だと、

python

import numpy as np
from scipy.special import comb

def B(n, p):
    _x_set = np.arange(n + 1)

    def _f(r):
        if r in _x_set:
            return comb(n, r) * p ** r * (1 - p) ** (n - r)
        else:
            return 0
    return _x_set, _f

って書くことが出来ますが、これは数学の世界ではこんな感じです。

$n$を自然数、$p$を $0<p<1$ なる実数とする。$r={0,1,...n}$に 値を取る確率変数$X$ について

P(X=r) := 
\left\{
\begin{array}
{}_nC_{r} p^r (1-p)^{n-r} &(if r\in{0,1,2,\cdots ,n})\\
0 &(otherwise)
\end{array}
\right.

によって確率分布が与えられるとき、$X$は二項分布$B(n,p)$に従う、という。

記述が似てますね。。
ちなみにこの確率変数は「同じ試行を$n$回独立に行うとする。この試行においてある事象Aが起こる確率を$p$とするとき、Aが$r$回$(0\leq r\leq n)$起こる確率」などで使用します。

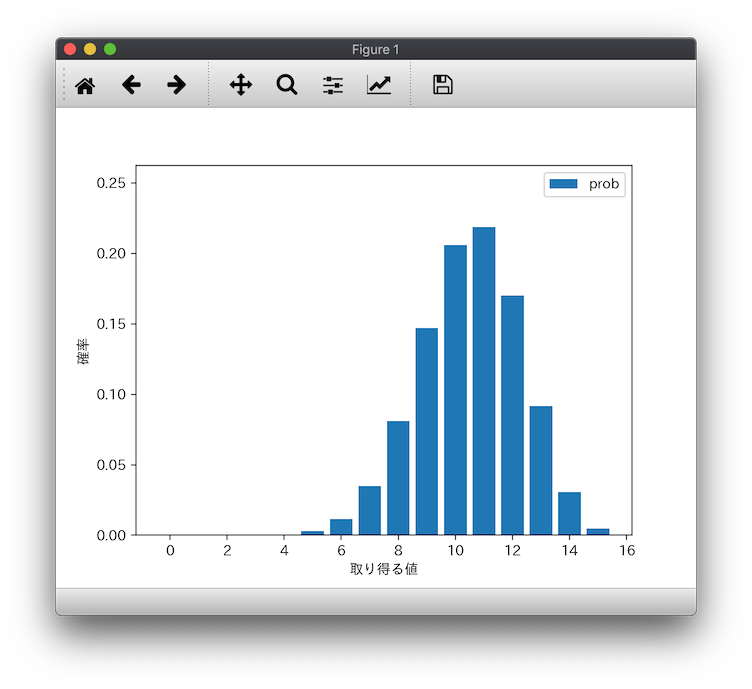
ついでに備忘のため、確率分布のグラフも書いておきます。

B.py

#!/usr/bin/env python
# -*- coding: utf-8 -*-

import matplotlib.pyplot as plt
import numpy as np
from scipy.special import comb
import sys

def main(args):
    # 確率変数を定義
    n = 15
    p = 0.7
    X = B(n, p)
    plot_prob(X)

def B(n, p):
    _x_set = np.arange(n + 1)

    def _f(x):
        if x in _x_set:
            return comb(n, x) * p ** x * (1 - p) ** (n - x)
        else:
            return 0

    return _x_set, _f

def plot_prob(X):
    x_set, f = X
    prob = np.array([f(x_k) for x_k in x_set])

    fig = plt.figure()
    ax = fig.add_subplot(1, 1, 1)
    ax.bar(x_set, prob, label='prob')
    ax.set_ylim(0, prob.max() * 1.2)

    ax.set_xlabel('取り得る値')
    ax.set_ylabel('確率')

    plt.legend()
    plt.show()

if __name__ == "__main__":
    main(sys.argv)

グラフが表示されれば、OKです!

実行環境

ちなみに実行環境の構築はこんな感じ。

$ sw_vers
ProductName:    Mac OS X
ProductVersion: 10.14.1 (Mojaveです)
BuildVersion:   18B75

Pythonの実行環境は適宜ご用意してもらえば結構ですが、以下、venvで環境を構築する手順を書いておきます。

$ python3 -m venv ./venv
$ source ./venv/bin/activate
(venv) $ which python3
/xxx/venv/bin/python3
(venv) $  python3 --version
Python 3.7.1
(venv) $ 

また、グラフを表示するために、Matplotlib を使用しますが、Macの環境構築に戸惑ったらこちらをご参照ください。

実行してみる

(venv) $ cat requirement.txt
matplotlib==3.0.2
numpy==1.15.4
scipy==1.1.0
PyQt5==5.11.3

(venv) $ pip install -r requirement.txt
... 割愛
(venv) $ python3 B.py

これでグラフが表示されるはずです。

確率変数の期待値と分散

数学に戻ります。離散型の確率変数$X$を

P(X=a_i) =P_i \quad (i=1,2,\cdots N, or \quad i=1,2,\cdots)\\
(ただし i \neq j \Rightarrow a_i \neq a_j ,\quad \sum_{i=1} P_i = 1)

とするとき

\begin{align}
E[X] :&=  \sum_{i=1} a_iP_i\\
V[X] :&= E[(X-E[X])^2]\\
&=\sum_{i=1}(a_i-E[X])^2  P_i
\end{align}

をそれぞれ$X$の期待値、分散という。

もっと一般的に、 $\mathbb{R}$上の実数値関数 $g(x)$があるとして、$x$に確率変数$X$を代入することで得られる$g(X)$という別の確率変数を考えるとき

\begin{align}
E[g[X]] &:=  \sum_{i=1} g(a_i)P_i \\
V[g[X]] &:=  \sum_{i=1}(g(a_i)-E[g[X]])^2  P_i
\end{align}

と定義します。

先の定義に従うと $V[X]$は、$E[g[X]]$の $g[X]:= (X-E[X])^2$ としたばあい、ってことですね。

、、、って数学の話がありますが、コレを実装するとこんな感じ。

def E(X, g=lambda x: x):
    """
    離散型確率変数の、期待値の定義
    :param X: 確率変数
    :param g: E[g[x]] とかって渡すときの関数
    :return:
    """
    x_set, f = X
    return np.sum([g(a_i) * f(a_i) for a_i in x_set])

def V(X, g=lambda x: x):
    """
    離散型確率変数の、分散の定義
    :param X: 確率変数
    :param g: V[g[x]] とかって渡すときの関数
    :return:
    """
    mean = E(X, g)
    return E(X, g=lambda x: (g(x) - mean) ** 2)

lambda式で関数を渡してあげることで、ほぼほぼ数学通りのコードになってますね。とくに$\sum$(np.sum)の繰り返しを 後置されたfor文でかける内包表記がステキです。

ところで$B(n,p)$の $E[X]$、$V[X]$は

\begin{align}
E[X] :&= np\\
V[X] :&= np(1-p)\\
\end{align}

となることが知られているので、上記の例ででてきた $B(15,0.7)$で計算してみます。

#!/usr/bin/env python
# -*- coding: utf-8 -*-

import matplotlib.pyplot as plt
import numpy as np
from scipy.special import comb
import sys


def main(args):
    # 確率変数を定義
    n = 15
    p = 0.7
    X = B(n, p)

    print(f'E(X) = {E(X):.3f}')  # 計算
    print(f'V(X) = {V(X):.3f}')  # 計算

    print(f'E(X) = {n * p:.3f}')  # 公式
    print(f'V(X) = {n * p * (1 - p):.3f}')  # 公式


def E(X, g=lambda x: x):
    x_set, f = X
    return np.sum([g(a_i) * f(a_i) for a_i in x_set])


def V(X, g=lambda x: x):
    mean = E(X, g)
    return E(X, g=lambda x: (g(x) - mean) ** 2)


def B(n, p):
    _x_set = np.arange(n + 1)

    def _f(r):
        if r in _x_set:
            return comb(n, r) * p ** r * (1 - p) ** (n - r)
        else:
            return 0

    return _x_set, _f


if __name__ == "__main__":
    main(sys.argv)

(venv) $ python3 B.py
x$ python3 B.py 
E(X) = 10.500
V(X) = 3.150
E(X) = 10.500
V(X) = 3.150
(venv) $ 

一致してますね。コード上の E(X),V(X) の定義もよさそうです。

二項分布の期待値と分散の公式の証明

Pythonと数学ってテーマと徐々にズレてってますが、このキレイな公式の証明の備忘。ついでに積率母関数もやっちゃう。うーん、前に書いた「Qiitaで数式がつかえるみたいなので...」みたいになってきたけど気にしません。

積率母関数 Mx(t)

確率変数$X$に対して、下記の関数を積率母関数と定義する:

\begin{align}
M_X(t) :&= E[e^{tx}], \quad  (- \infty < t < \infty)\\
&= \sum_{i=1}^{N} e^{ta_i} p_i
\end{align}

こう定義すると、下記のとても面白い性質

\begin{align}
\frac{d^n}{dt^n}M_X(0)&=
\left.
 \frac{d^n}{dt^n} \sum_{i=1}^{N} e^{ta_i} p_i
\right|_{t=0}\\
&=
\left.
 \sum_{i=1}^{N} (a_i)^ne^{ta_i} p_i
\right|_{t=0}\\
&=
 \sum_{i=1}^{N} (a_i)^n p_i\\
&= E[X^n]\\
\end{align}

が得られます。

では「二項分布の積率母関数」を定義に従って計算してみます。取り得る値$r$は $r={0,1,...n}$ なので、、

\begin{align}
M_X(t) &= \sum_{r=0}^{n} e^{tr} \times{}_nC_{r} p^r (1-p)^{n-r}\\
&= \sum_{r=0}^{n} {}_nC_{r} (pe^t)^r (1-p)^{n-r}\\
&= (pe^t+q)^n , &q:=(1-p) \\
\end{align}

ちなみに最後のは

 \sum_{r=0}^{n} {}_nC_{r} x^r y^{n-r} =(x+y)^n 

であるためです。ねんのため。

ようやく二項分布の期待値と分散の公式の証明

したがって、

\begin{align}
M'_x(t) &= np(pe^t+q)^{n-1}e^t\\
M''_x(t)&= np^2(n-1)(pe^t+q)^{n-2}e^te^t + np(pe^t+q)^{n-1}e^t\\
&= np\{p(n-1)(pe^t+q)^{n-2}e^{2t} + (pe^t+q)^{n-1}e^t\}\\
&\\

M_X'(0) &= np\\
M_X''(0) &= np\{p(n-1) + 1\}\\
&= n (n-1)p^2 + np
\end{align}

(関数の積の微分とか久しぶり:-))
よって、

$B(n,p)$の $E[X]$、$V[X]$は

\begin{align}
E[X] &= M_X'(0) = np\\
V[X] &= M_X''(0) - (M_X'(0) )^2\\
&=n (n-1)p^2 + np - (np)^2\\
&=np-np^2\\
&=np(1-p).\\
(Q.E.D.)

\end{align}

($V[X] = E[X^2]-(E[X])^2$などはもう自明って事で)

確率分布の1000回試行をグラフにしてみる

先に出てきたステキな記述、

trial_count = 1000
sample = np.random.choice(x_set, trial_count, p=prob)  # サイコロをふる試行を、trial_count 回やった結果を取得。

についてホントに確率分布通りに試行が実施されているかを確認してみます。$E[X],V[X],B(n, p)$ あたりのpythonコードは変わらないので以下省略。

B.py

#!/usr/bin/env python
# -*- coding: utf-8 -*-

import matplotlib.pyplot as plt
import numpy as np
from scipy.special import comb
import sys


def main(args):
    # 確率変数を定義
    n = 15
    p = 0.7
    X = B(n, p)

    print(f'E(X) = {E(X):.3f}')  # 計算
    print(f'V(X) = {V(X):.3f}')  # 計算

    print(f'E(X) = {n * p:.3f}')  # 公式
    print(f'V(X) = {n * p * (1 - p):.3f}')  # 公式

    plot_prob(X)


def plot_prob(X):
    x_set, f = X
    prob = np.array([f(x_k) for x_k in x_set])

    fig = plt.figure()

    ax1 = fig.add_subplot(2, 1, 1)

    # 一つ目は、取り得る値とその確率の折れ線グラフ
    ax1.plot(x_set, prob, label='prob')

    # 二つ目は、この確率の試行を1000回繰り返したデータ、の相対度数化したデータをヒストグラム化
    samples = np.random.choice(x_set, 1000, p=prob)
    weights = np.ones_like(samples) / len(samples)
    ax1.hist(samples, bins=100, range=(0, len(x_set)), weights=weights, label='サンプリング')

    ax1.vlines(E(X), 0, 1, label='E[X]', colors='Gray')
    ax1.set_xticks(np.append(x_set, E(X)))

    ax1.set_ylim(0, prob.max() * 1.2)

    ax1.set_xlabel('取り得る値')
    ax1.set_ylabel('確率')
    # 取り得る値と、それぞれの確率をプロット
    plt.legend()

    ax2 = fig.add_subplot(2, 1, 2)

    #  下のヒストグラムは、200コのサンプリングの平均をとる、ってのを10,000回試行した結果
    sample_count = 200
    sample_means = [np.random.choice(x_set, sample_count, p=prob).mean() for _ in range(10000)]

    print(sample_means)
    weights2 = np.ones_like(sample_means) / len(sample_means)

    freq, _, _ = ax2.hist(sample_means, bins=100, range=(10, 11), weights=weights2, label='標本平均のサンプリング')

    ax2.vlines(E(X), 0, 1, label='E[X]', colors='Gray')
    ax2.set_ylim(0, 0.04)
    ax2.set_xticks(np.append(x_set, E(X)))
    ax2.set_xlim(10, 11)
    ax2.set_xlabel('標本平均')
    ax2.set_ylabel('相対度数')

    plt.tight_layout()  # タイトルの被りを防ぐ
    plt.legend()
    plt.show()

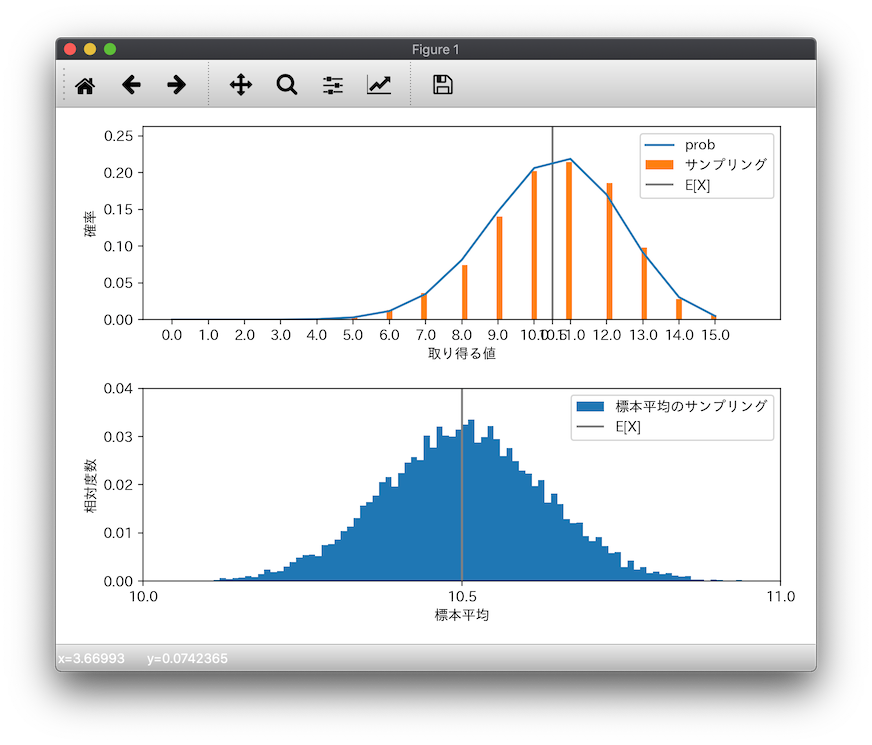
実行してみると、以下が得られました。

先ほどは確率分布を棒グラフで書きましたが、今回は確率(prob)は折れ線グラフにして、サンプリングした相対度数をオレンジの棒グラフにしました。
1,000回の試行で、ちゃんと確率分布どおりに分布してそう、ということがわかります。

また下のヒストグラムは、200コのサンプリングした結果の平均を求める、という試行を10,000回繰り返した結果の相対度数です。標本平均は、$E[X]$ つまり確率分布の期待値10.5に収束しそうにみえますねー。。

まとめ

こんな感じで

• 内包表記を使ったnp.sumって、まさに$\sum$ の書き方にそっくり
• 確率の試行とかを意識したnp.random.choiceの記法
• 関数を渡すことで $E[g[X]]$などをうまく表現出来る
• そもそもグラフが簡単にかけるから、理論と実験を視覚的に把握出来る

あたりが、数学とPythonって似てるっていうかとても親和性高いんだねー、、って話でした。が、気がつくと統計の備忘録みたいになっちゃってますね。

おつかれさまでした。。

関連リンク

• Pythonで理解する統計解析の基礎 Pythonつかって統計の再勉強中。
• 数理統計入門 1990年の本ですが、理論もまあまあ詳しく書いてあってとてもわかりやすいです
• Qiitaで数式がつかえるみたいなので三角関数とか内積とか相関係数について書いて、Pythonで計算してみた