はじめに
ECCV2020より以下の論文
[1] B. Mildenhall, et. al. NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis.
のまとめ
arXiv:
https://arxiv.org/abs/2008.02268
発表されて時間がたっていることもあり、既に多くのまとめが存在する。
@takoroy氏のまとめ:
https://qiita.com/takoroy/items/53e62d303b9743b06801
Albertのofficial blogで山内氏の記事
https://blog.albert2005.co.jp/2020/05/08/nerf/
よって、ここではこれらのまとめや論文では言及されていない点に関して重点的にまとめる。具体的には以下
- (1)式のT(t)に関して
- (1)式から(3)式への変形に関して
概要
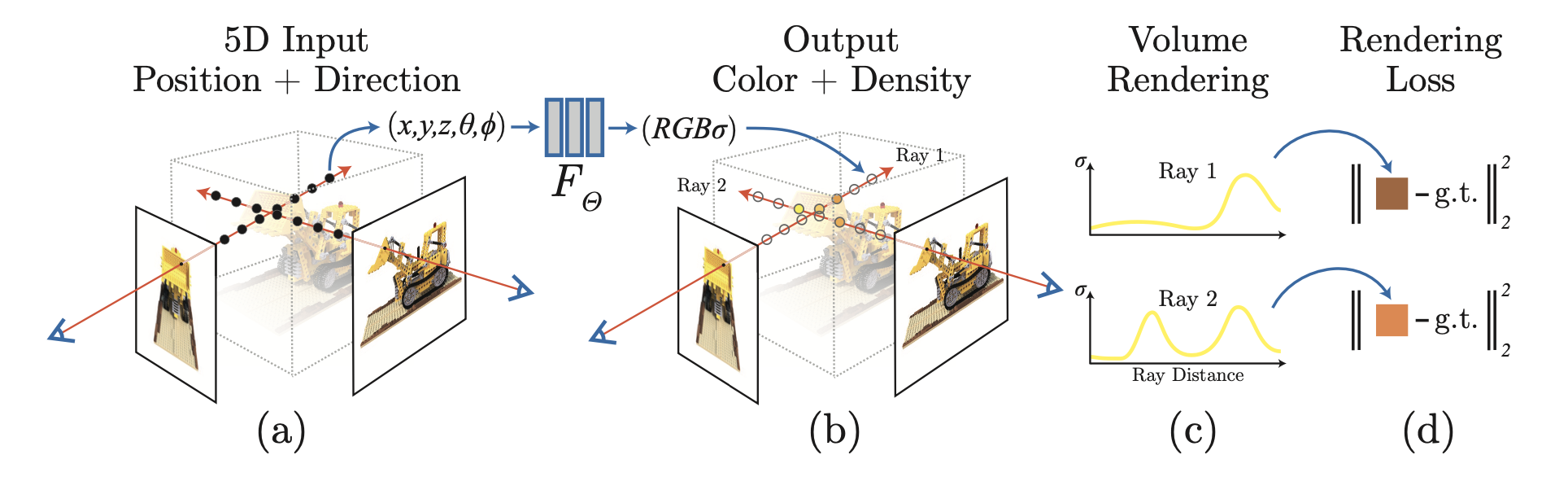
- ある空間上のシーンを写した複数の画像から別の視点からの画像を生成するしくみ
- 新たに提案した 5D neural radiance fieldsという場を考え、これを学習によって取得する
- 旧来のレンダリングを使って表現する
- multi-cameraからの画像以外に、1)カメラの内部パラメータ、2)カメラの外部パラメータ、3)scene bounds?を利用する。推論時はCOLMAPを使ってこれらを推定する
neural radiance field を超ざっくりまとめ
まず、色と密度からなるベクトル場を考える。
${\bf c} = (r,g,b)$ :色
$\sigma \in \mathbb{R}$ :密度
密度は場所によって異なるので位置 ${\bf x} = (x,y,z)$ のみに依存すると考える。
$\sigma ({\bf x})$。
一方、色は場所と向きによって変わると考える。(つまりランバート反射でない)
${\bf c}({\bf x}, {\bf d})$
画像上のある点の色は焦点とその点を結ぶ直線状の光の積算と考える。ただし途中で吸収される分も考慮。
この直線上の dt から発せられる光を $\sigma({\bf r}(t), {\bf d}) dt$ とすると、画像上のある点の色は
C({\bf r}) = \int_{t_f}^{t_n} T(t) \sigma({\bf r}(t), {\bf d}) dt , {\rm where} \ T(t) = \exp{\left( - \int_{t_n}^{t} \sigma (s) ds \right)} \tag{1}
$T(t)$ に関しては後述。
(1)式のT(t)に関して
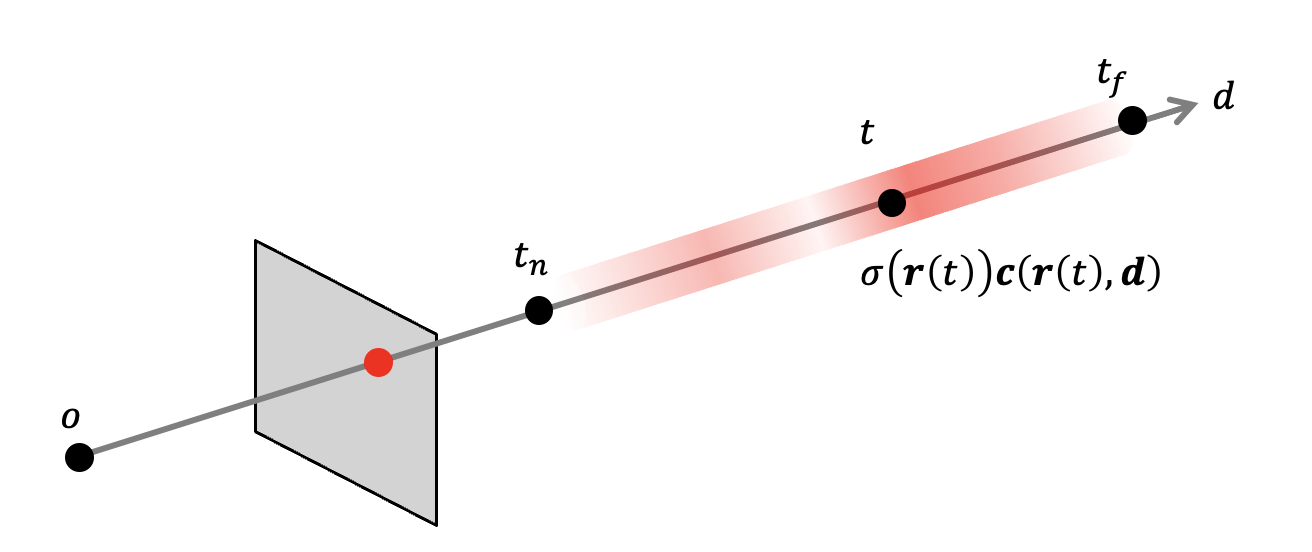
まず以下のようにカメラの焦点 o から物体を見るピンホールモデルにおいて、d方向を見た場合に、その直線上に存在する物体の密度σと色cが位置 ${\bf r}(t)$ などの関数で表されている。
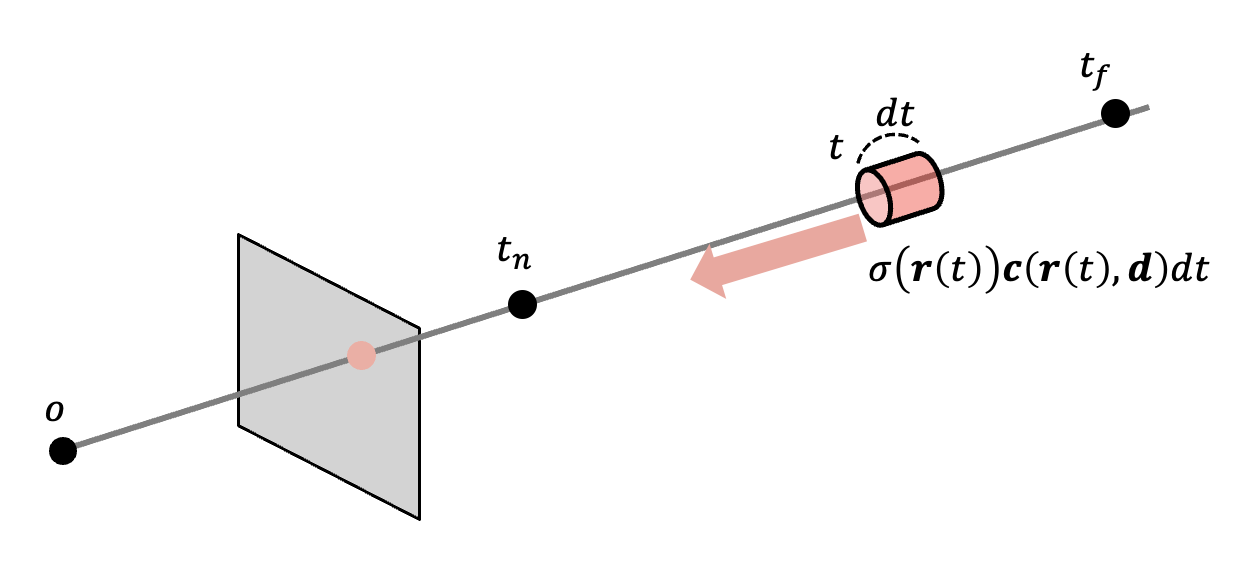
途中で遮るものがなければ、これらの色・密度の積分が画像上に色として表されるだろう。いま、以下のように位置 t における微小な要素 dt を考えると、
この部分のみからくる光は $\sigma ({\bf r}(t)) {\bf c}({\bf r}(t), {\bf d}) dt$ と考えられる。いかし実際にはその間に物体(の密度σ)が存在するため、光の強度が落ちるだろう。
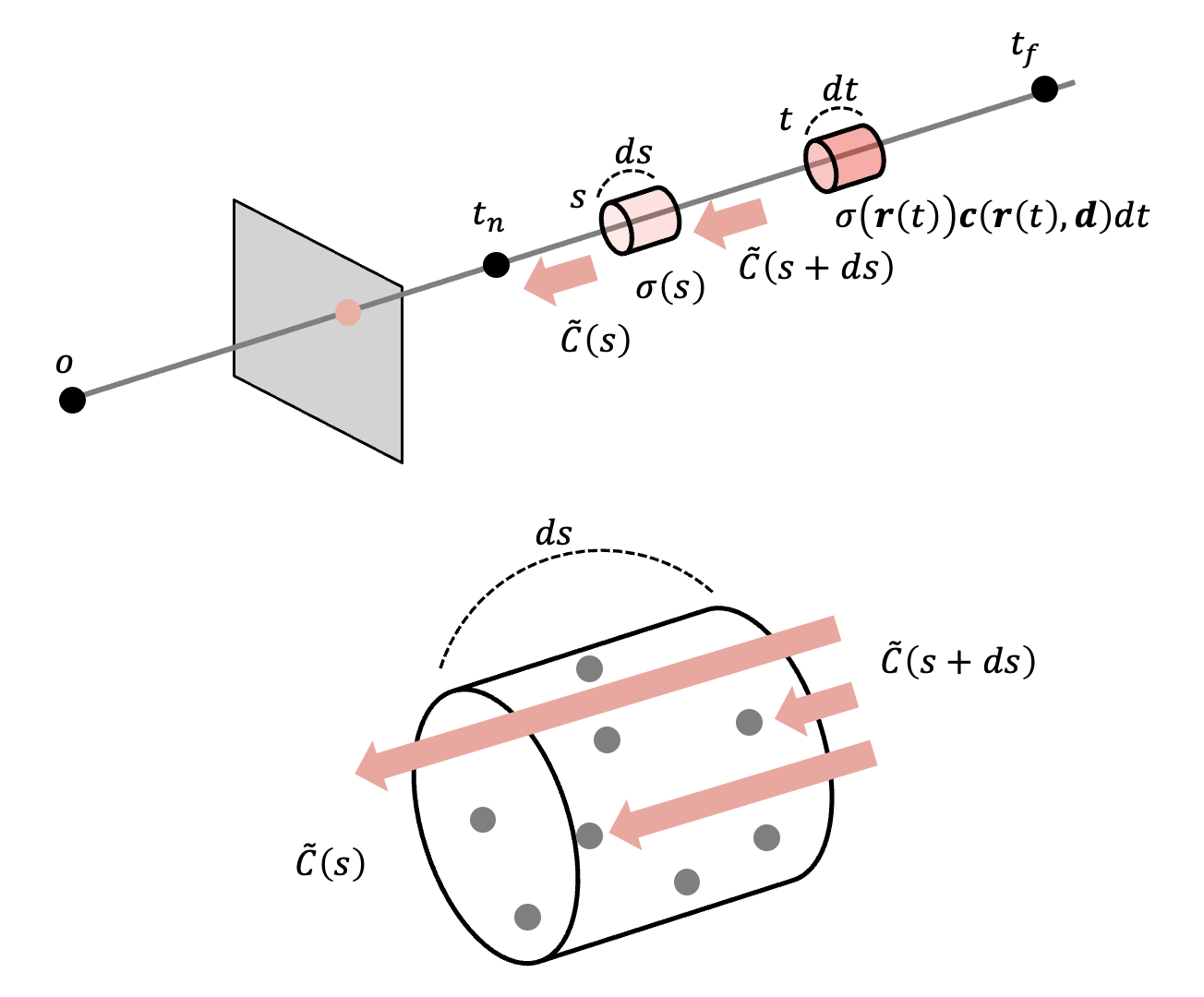
そこで以下のように t と画像間にある微小区間 ds を考える。
s + ds から入射した光は一定の確率で粒子にぶつかり、残りが s から出ると考えると、光の減少率は物質量 $\sigma ({\bf r}(s))ds$ となるだろう。
\frac{d \tilde{C}}{\tilde{C}} = \sigma (s) ds
これを $t_n$ から t まで積分して
\begin{eqnarray}
\int_{\tilde{C}_{t_n}}^{\tilde{C}_{t}} \frac{d \tilde{C}}{\tilde{C}} &=& \int_{t_n}^{t} \sigma (s) ds \\
\ln \frac{\tilde{C}_{t}}{\tilde{C}_{t_n}} &=& \int_{t_n}^{t} \sigma (s) ds \\
\ln \frac{\tilde{C}_{t_n}}{\tilde{C}_{t}} &=& - \int_{t_n}^{t} \sigma (s) ds \\
T(t) &=& \frac{\tilde{C}_{t_n}}{\tilde{C}_{t}} = \exp{\left( - \int_{t_n}^{t} \sigma (s) ds \right)}
\end{eqnarray}
これが (1) 式の右。
(1)式から(3)式への変形
(3)式左辺でいきなり exp が出てきて違和感があるので、
\sigma_i \delta_i \approx \left( 1 - \exp{\left( - \sigma_i \delta_i \right)} \right)
を示す。
ネイピア数の定義より
\begin{eqnarray}
\lim_{n \to \infty} \left( 1 + \frac{1}{n} \right)^n = e
\end{eqnarray}
で $n = - \frac{1}{\sigma_i \delta_i} $ として
\begin{eqnarray}
\lim_{n \to \infty} \left( 1 + \frac{1}{n} \right)^n = \lim_{- \sigma_i \delta_i \to 0} \left( 1 + \left( - \sigma_i \delta_i \right) \right)^{- \frac{1}{\sigma_i \delta_i}} &=& e \\
\end{eqnarray}
$- \sigma_i \delta_i$ が十分小さいとき・・・つまり δ の区間を十分小さくとると
\begin{eqnarray}
\left( 1 - \sigma_i \delta_i \right)^{- \frac{1}{\sigma_i \delta_i}} &\approx& e \\
1 - \sigma_i \delta_i &\approx& \exp{\left( - \sigma_i \delta_i \right) } \\
\sigma_i \delta_i &\approx& 1 - \exp{\left( - \sigma_i \delta_i \right) } \\
\end{eqnarray}
よって成立。
その他 memo
- dataset は DeepVoxels dataset など
- 定量的評価のメトリクスは PSNR, SSIM, LPIPS