はじめに
BMVC 2016 から以下の論文
[1] B. Tekin, et. al."Structured Prediction of 3D Human Pose with Deep Neural Networks", BMVC 2016
のまとめ
arXiv:
https://arxiv.org/abs/1605.05180
コード：
所在は不明
日本語のまとめ記事：
DeNAのざっくりまとめ
https://engineer.dena.jp/#tekin2016
ちなみにBMVC は British Machine Vision Conference の略で、こちらのサイト
http://www.guide2research.com/topconf/
によるとH-indexが46とそこそこのカンファレンス。
概要
- 単眼カメラからの画像から３次元の姿勢を推定するモデル
- 事前にautoencoderで姿勢の潜在表現を学習する
- この潜在表現を利用して３次元の姿勢を回帰問題として解く
（[1]Figure3より）
左側の入力画像に対して、その右がground truth、さらに右が本手法で推定した３次元骨格。
手法の解説
全体像
全体像は以下の図。
（[1]Figure1より）
解説に書いてる通り、以下の３段階で学習を行う。
- 潜在変数の次元が大きいAuto-encoderで人の姿勢を学習する
- その潜在変数をtargetとし、画像を入力としたCNNを学習する
- decoderを付け加えて姿勢を再学習する
1. auto-encoderによる姿勢の学習
以下の図のようにauto-encoderで姿勢を学習する。
（[1]Figure2より抜粋）
人の関節のベクトル $y_i$ に等方性のノイズを加えたものを $\tilde{y}_i$ 、それをパラメータ $\theta_{ae}$ の auto-encoder $f_{ae}$ により再構築されたものを $\hat{y}$ とすると、
\hat{y} = f_{ae} (y, \theta_{ae})
$\theta_{ae}$ のパラメータのうち、重みに関しては、過適合を防ぐため
W_{dec,j} = W^T_{enc,j}
とする。
loss は入力した骨格と再構築した骨格との２乗誤差にencoderのヤコビ行列に対し行列ノルムの２乗を加える。
\newcommand{\argmin}{\mathop{\rm arg~min}\limits}
\theta_{ae}^* = \argmin_{\theta_{ae}} \sum^N_i \|y_i - f(y_i, \theta_{ae} \|^2_2 + \lambda \| J(y_i) \|_F^2
このノルムは初めて見たが、ヤコビ行列は $J(y) = \frac{\partial g}{\partial y}(y)$ と、出力を入力で微分してるから重みみたいなものと考えると、そのノルムを取ってるだけなので、重みに対してL2 norm の２乗を取ってるみたいなもん？？
2. 潜在空間を回帰で学習する
第２段階として、下図
（[1]Figure2より抜粋）
のようにauto-encoder のlatentをtargetとした回帰問題としてCNNを学習する。
このCNNモデルを $f_{cnn}(x_i, \theta_{cnn})$ として loss は
\newcommand{\argmin}{\mathop{\rm arg~min}\limits}
\theta_{cnn}^* = \argmin_{\theta_{cnn}} \sum^N_{i} \| f_{cnn} (x_i, \theta_{cnn}) - h_{L,i} \|^2_2
とする。
3. decoderを加えて姿勢を再学習する
３段階目として以下の図
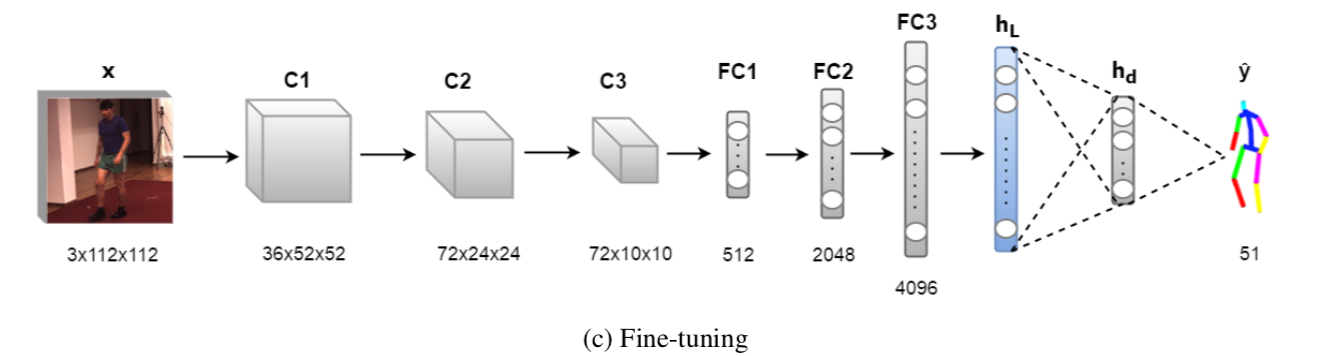
のように auto-encoder の decoder 部分を付け加えてfine-tuningする。
lossは targetの関節位置と推論の位置とで２乗誤差をとる。
\newcommand{\argmin}{\mathop{\rm arg~min}\limits}
\theta_{ft}^* = \argmin_{\theta_{ft}} \sum^N_i \| f_{ft} (x_i, \theta_{ft} ) - y_i \|^2_2
実験と結果
実験の概要
- dataset・・・Human3.6M
- metrics・・・３次元ユークリッド距離の平均値
他モデルとの比較結果
（[1]Table1より）
2016年当時の他の手法と比較して値がよい。