はじめに
CoRL2020(Conference on Robot Learning) から以下の論文
[1] H. Li, et. al. "Unsupervised Monocular Depth Learning in Dynamic Scenes"
のまとめ
last author はこの分野で有名な Anelia Angelova 氏。
arXiv:
https://arxiv.org/abs/2010.16404
github(公式コード):
https://github.com/google-research/google-research/tree/master/depth_and_motion_learning
tensorflow 1系で書かれてる
概要
- 単眼RGBビデオカメラからdepth map、カメラの外部行列、移動物体のmapを推定するモデル
- これまでのdepthモデルと異なり移動物体のmaskやbouding boxは必要ない
- 代わりに2種類の正則化を用いている
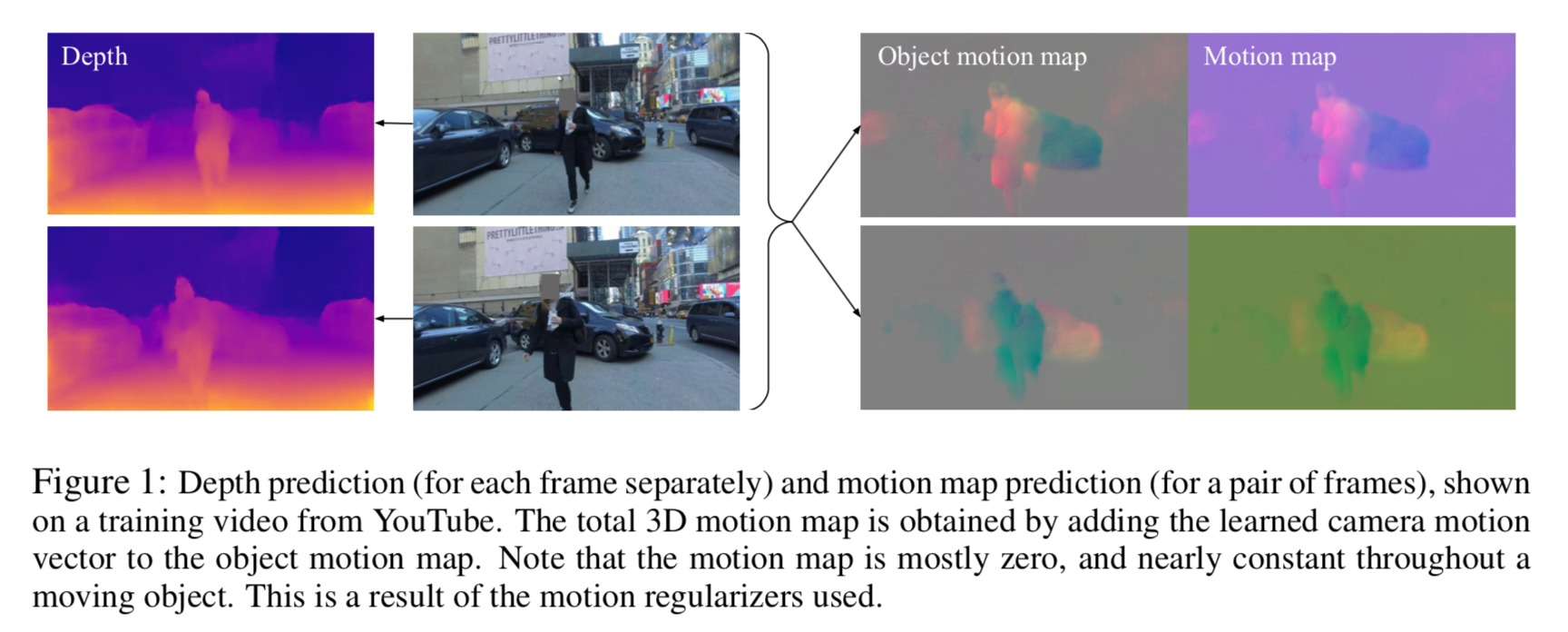
以下の図のように
左から2列目の連続した2フレームの入力画像に対して、それぞれその左のようなdepth mapを推定する。
一方入力画像2つからその右 object motion mapやmotion mapを推定する。motion mapは正則化の効果が効いていて、ほとんどがゼロであるのと同時に各移動物体の中ではconstな値となる。
アーキテクチャ
全体像
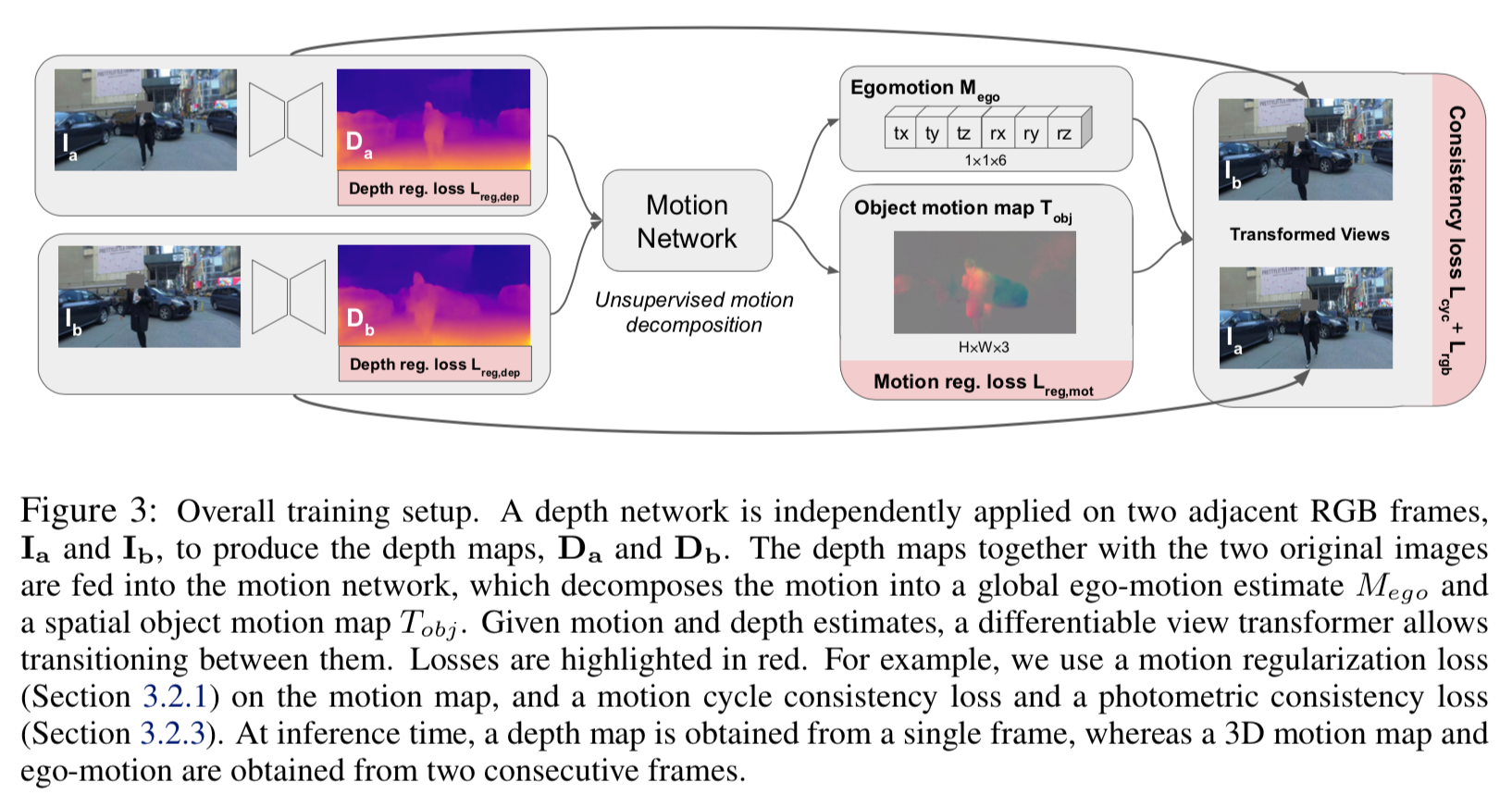
モデルのアーキテクチャ全体像は以下。
最左 original 画像に対して、depth network で depth mapを出力する。連続する2フレームのdepth mapと original 画像からmotion network でego-motionの6つのパラメータとobject motion mapを推定する。
これらから一方の画像をwarpさせ、もう一方の画像の推定値を得る。
Depth network
- encoder decoder 構造
- 最後の活性化関数はsoftplus
- 各reluの前にrandomized layer normalizationを行う
Motion network
loss
preliminary
用語の定義
$I_a$ :1フレーム目の画像
$I_b$ :2フレーム目の画像
$(u,v)$ :画像上の座標
$D(u,v)$ :depth networkから推定したdepth map
$T_{obj}(u,v)$ :motion prediction networkから推定した移動物体の3次元平行移動ベクトル
$M_{ego}$ :ego-motionにおける回転行列の3オイラー角と平行移動ベクトルの3要素からなる6つのパラメータ
$\bf{R}$ :回転行列(ego-motionおよび移動物体とも共通)
$T_{ego}$ :ego-motionにおける3次元平行移動ベクトル
$T(u,v) = T_{obj}(u,v) + T_{ego}$ :カメラに対して相対的な移動物体の平行移動ベクトル
$d(u,v) = 1/D(u,v)$ :disparity
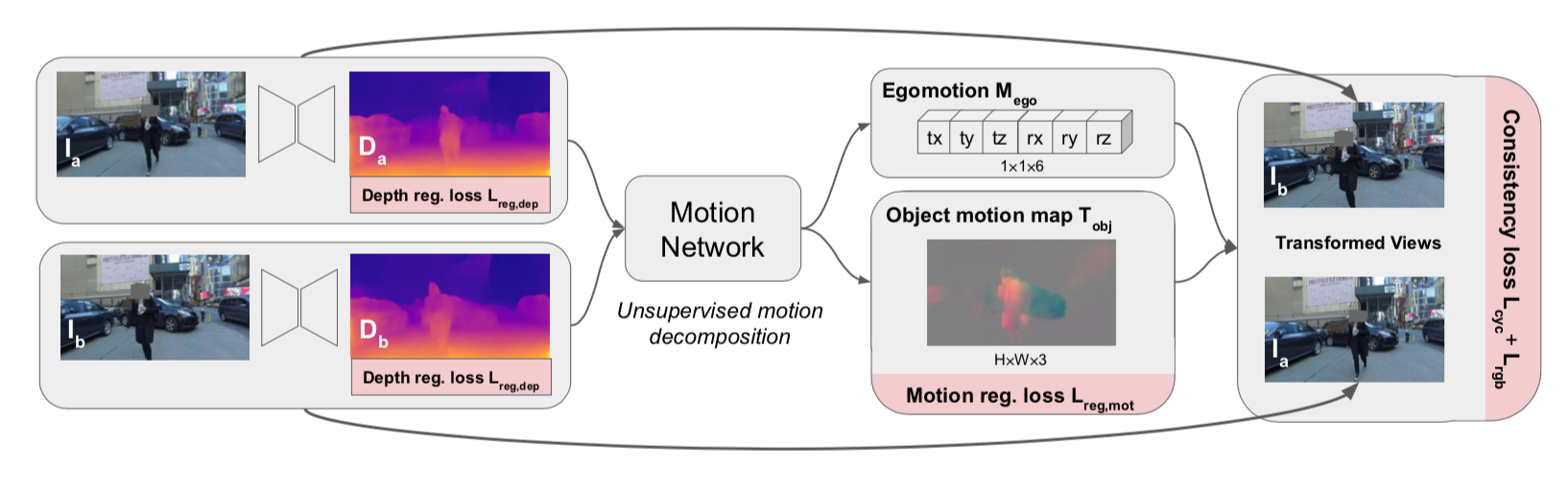
改めてこちらの図。赤い部分がloss。
まず左から、depth mapに対しては Depth regularization loss $L_{reg, dep}$ を計算する。
中より右、Object Motion mapに対しては Motion regularization loss $L_{reg, mot}$ を計算する。
最右、warpして生成した画像に対しては cycle consistency loss $L_{cyc}$ と photometric consistency loss $L_{rgb}$ を計算する。
以下書くlossを細かく見ていく。
Motion Regularization loss
この論文の主題。
これまでの先行研究では移動物体の領域を特定するために外部で推定したsegmentやbounding boxを用いたが、本論文ではそれは用いず、正則化で代用する。
Motion regularization loss $L_{reg, mot}$ は2つの項から構成される。
1つが group smoothness loss $L_{g1}$ 。
もう1つが sparsity loss $L_{1/2}$ 。
group smoothness loss
各移動物体は剛体的に動く・・・つまりその物体内の移動は同様である・・・という事前知識を利用したもの。
L_{g1} [T(u,v)] = \sum_{i \in \{x,y,z \}} \int \int \sqrt{ \left( \partial_u T^i_{obj} (u,v) \right)^2 + \left( \partial_v T^i_{obj} (u,v) \right)^2 } dudv
物体の全ピクセルにわたって、u方向の変化の2乗、v方向の変化の2乗を足していく。そのルートを計算しているので、2次元的な増加を求めている。
$T^i_{obj}(u,v)$ は3次元ベクトルなので、最後に全ての成分にわたって足す。
論文では $T_i(u,v)$ となっているが、カメラからの相対的な平行移動ベクトルと区別するため、あえて $T_{obj}(u,v)$ とした。
sparsity loss
移動物体があるところは $T_{obj}$ の絶対値が大きいが、移動物体がないところは0なので、そのようにスパースにしたい。L1よりスパース性が強力なL 1/2 を用いる。
$\langle |T^i_{obj}|\rangle$ を $T^i_{obj}(u,v)$ の平均値として
L_{1/2} [T(u,v)] = 2 \sum_{i \in \{x,y,z \}} \langle |T^i_{obj}| \rangle \int \int \sqrt{ 1 + |T^i_{obj}(u,v)| / \langle |T^i_{obj}|\rangle } dudv
Depth Regularization
論文[2]など最近の論文と同様、edge-awareなsmoothness 正則化をdepth mapに適応する。
L_{reg, dep} = \alpha_{dep} \int \int (|\partial_u d(u,v) | e^{-|\partial_u {\bf I}(u,v)|}) + (|\partial_v d(u,v) | e^{-|\partial_v {\bf I}(u,v)|})dudv
expの中が元画像の変位の負となっているので、元画像に変位があるところはexp部分がほぼほぼゼロとなり、学習対象から外される。つまり元画像の変化がない(おおよそ同じ物体の場所)に対してのみ平滑化する。
Consistency Regularization
Lossのメイン部分。cycle consistency loss $L_{cyc}$ と photometric consistency loss $L_{rgb}$ からなる。
cycle consistency loss
cycle consistency lossの考え方は、A frameからB frameへのtransformに対し、B frameからA frameへのtransoformはちょうど逆になるだろう、という発想。
B frameからA frameへの回転行列を ${\bf R}_{inv}$ 、同平行移動ベクトルを $T_{inv}$ として、
L_{cyc} = \alpha_{cyc} \frac{\| {\bf R R}_{inv} - \mathbb{1} \|^2}{\| {\bf R} - \mathbb{1} \|^2 + \| {\bf R}_{inv} - \mathbb{1} \|^2} + \beta_{cyc} \int \int \frac{\| {\bf R}_{inv} T(u,v) + T_{inv}(u_{warp}, v_{warp}) \|^2}{\| T(u,v) \|^2 + \| T_{inv}(u_{warp},v_{warp} \|^2 }dudv
まず第1項目から考える。分子は ${\bf R R}_{inv}$ なので、AからBへの回転行列とBからAへの回転行列が正しく推定できていれば、回した後に逆に回して元に戻るので、単位行列となるはず。
よって ${| \bf R R}_{inv} - \mathbb{1} |^2$ は理想的には0となるはず。よってこれをlossとする。
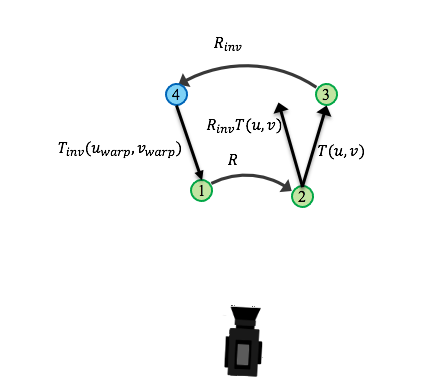
次に第2項目を考える。以下の図はカメラを固定して考えたときの、背景中の物体の相対的な変化。
frame A の位置①から回転行列 ${\bf R}$ で位置②となり、平行移動ベクトル $T(u,v)$ で③の位置となる。
一方、frame B からframe A へ移動させる場合は、位置③から回転行列 ${\bf R}_{inv}$ で位置④となり、平行移動ベクトル $T_{inv}(u_{warp},v_{warp})$ で位置①となる。
いずれの推論もうまくいっていれば、
{\bf R}_{inv} T(u,v) + T_{inv}(u_{warp}, v_{warp}) = {\bf 0}
となるはず。この大きさの2乗が第2項目の分子。それを各ベクトルの大きさの2乗で割って正規化している。
平行移動ベクトルの方は背景や各物体によって値が違うので、それらを積分する。
occlusion-aware photometric consistency loss
photometric consistency lossは論文[3]で提案されたocclusion-awareな仕組みを使う。
参考:拙著記事
https://qiita.com/masataka46/items/23d8652f356361d66c2f
それとSSIM使った類似度との和。SSIMに関してはこちら
https://qiita.com/masataka46/items/cf5f8ad3175cd1a1ab49
にまとめました。
L_{rgb} = \alpha_{rgb} \int \int | {\bf I}(u,v) - {\bf I}_{warp}(u,v) | \mathbb{1}_{D(u,v) > D_{warp}(u,v)} dudv + \beta_{rgb} \frac{1- SSIM( {\bf I} , {\bf I}_{warp})}{2}
実験と結果
- NVIDIA V100、480x192の解像度で190fpsの推論速度
- メトリクスのコードは Struct2Depth[4]を使用
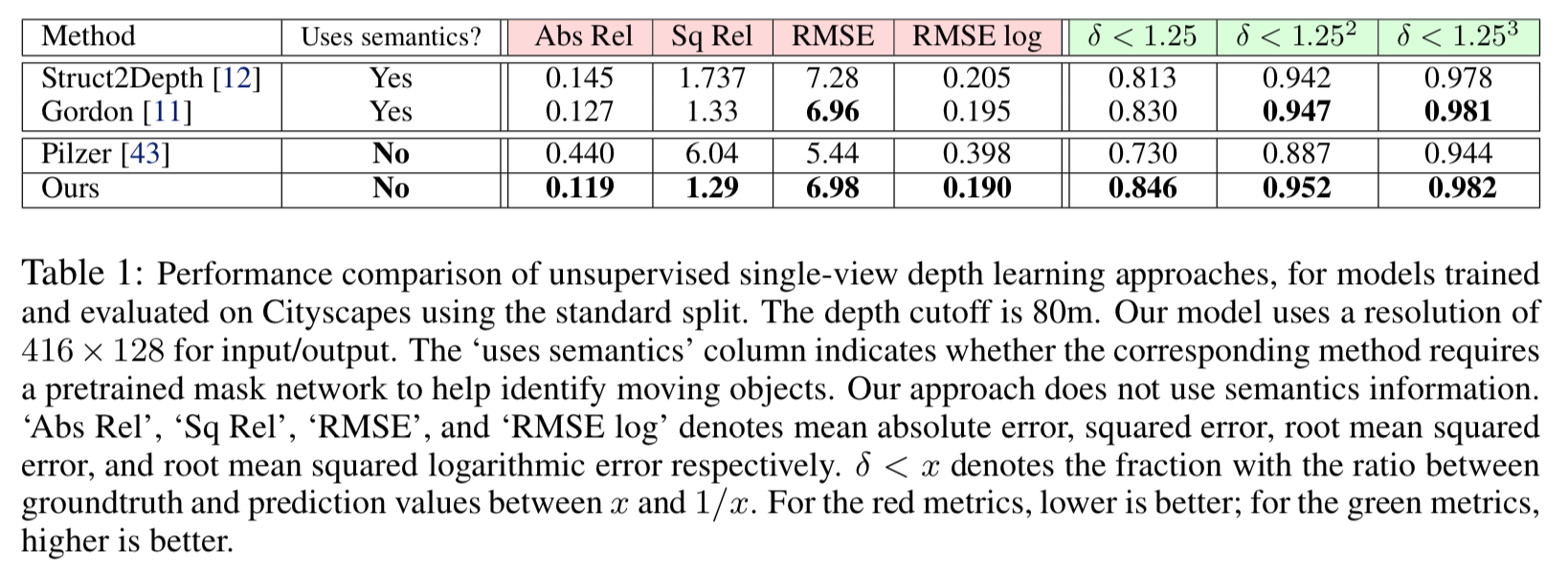
CityScapesを用いた定量的評価
CityScapes の test data を用いた他モデルとの比較は以下
本手法は移動物体に対するmaskを使わないが、使用するGordonら[3]の手法と比べても少しよい。
ablation study
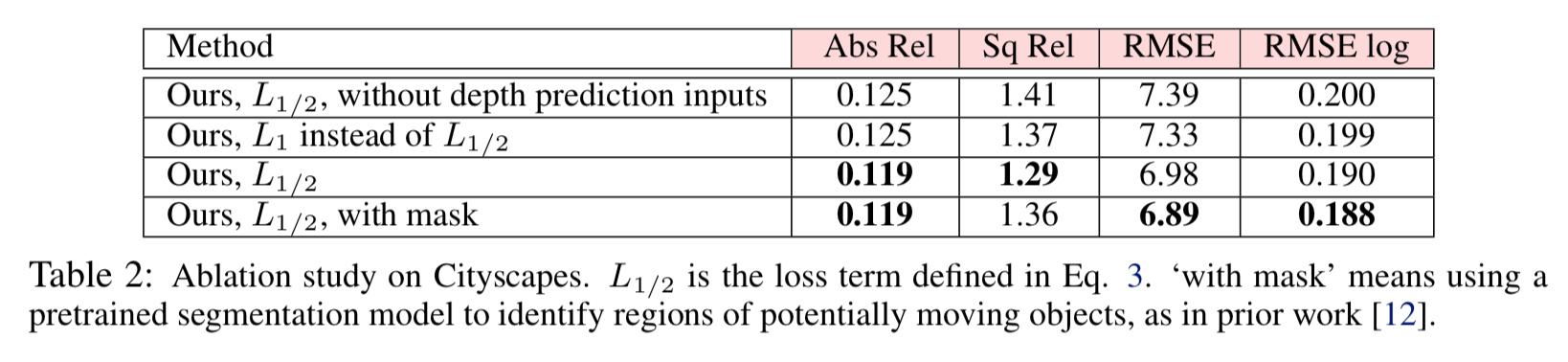
以下は1/2 正則化の効果を示した表。
まず最下段、マスクを用いた場合と、その上用いない場合では、精度がそれほど違わない。 -> マスクは無くても精度が良い。
上から2段目のL1とその下L1/2とを比較すると、L1/2の方が精度が良い。
最上段はL 1/2を使うが、motion prediction networkの入力としてdepth mapを用いない場合だが、3段目と比較すると精度が落ちる -> depth mapの入力は有効。
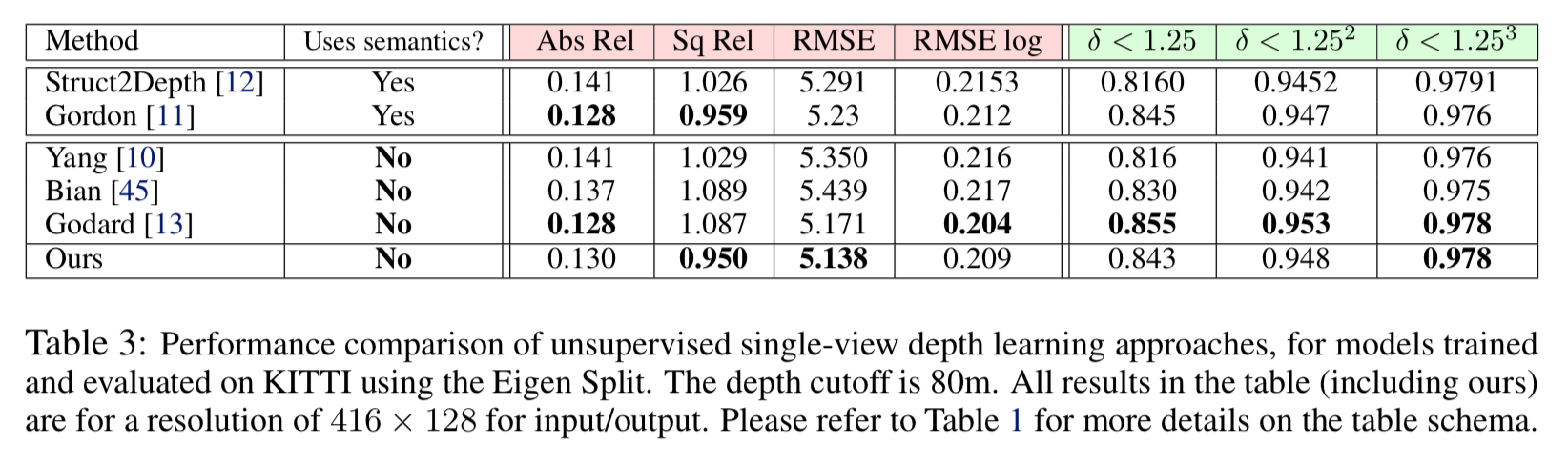
KITTI datasetを用いた定量的評価
KITTI datasetに対して推論(training dataとしては使ってない)させた場合の評価値は以下。
他のSOTAな手法と同等。 -> Cityscapesの場合と違って同等なのはなぜ?
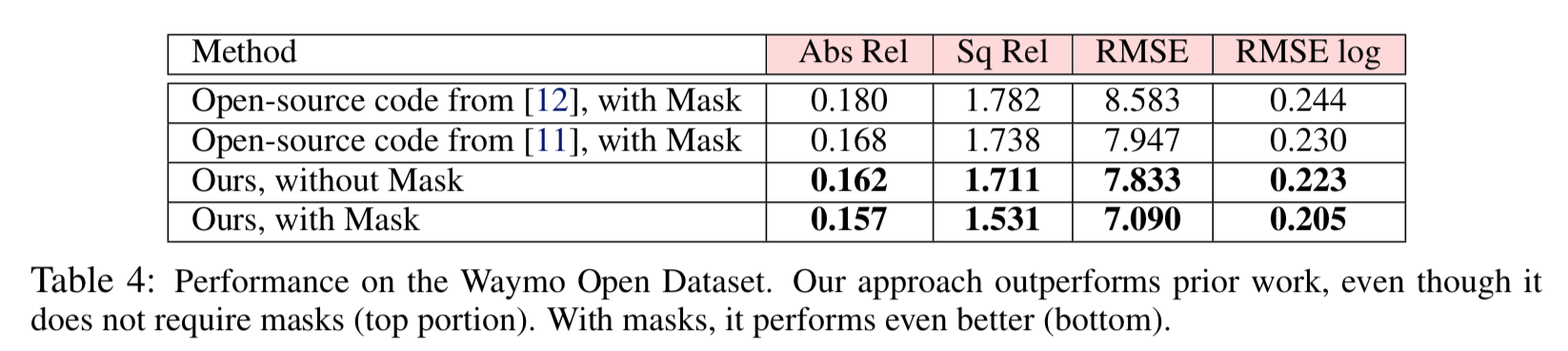
Waymo Open datasetを用いた定量的評価
このdatasetは車載カメラからのdatasetの中では現在最も巨大かつin the wildだそう。中には夜のシーンもある。
結果は以下。
maskが無くても既存手法を上回っている(1/2 正則化とかが有効)が、あると更に精度がよい。
Youtube 動画に対する定性的評価
Youtubeから適当にとってきた動画はカメラの内部座標もdepthのアノテーションもないが、以下のように推定できている。
結論
今回提案された正則化の効果は高い。これはマスク使う等の別のモデルにも導入できるので、応用範囲が広そう。
reference
[2] C. Godard, O. Mac Aodha, and G. J. Brostow. Unsupervised monocular depth estimation with
left-right consistency. In CVPR, pages 270–279, 2017.
[3] A. Gordon, H. Li, R. Jonschkowski, and A. Angelova. Depth from videos in the wild: Unsupervised monocular depth learning from unknown cameras. In ICCV, October 2019.
[4] V. Casser, S. Pirk, R. Mahjourian, and A. Angelova. Depth prediction without the sensors: Leveraging structure for unsupervised learning from monocular videos. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 33, pages 8001–8008, 2019.