Leafletでマンデルブロ集合の表示してみる (1)

はじめに

突然ですが、なんの脈絡もなく、マンデルブロ集合を描きたくなりました。
マンデルブロ集合 (Wikipedia)

↓こんなやつ↓

ただ描くだけだと面白くないので、Google Mapみたいにスクロールしたり拡大したり…というのをやってみよう…と思いちょっと手を動かしてみました。

先に完成品…

先に完成品をリンクしておきます。目標としては、このリンク先のようなことをやりたい、ということになります。

技術選定

Google Mapみたいな地図のアプリを作る、となると、いくつか選択肢はありますが、今回はタイル画像を用意してLeafletを使ってブラウザ上に描画する、という方法をとってみることにしました。

タイル画像

地図アプリで一般的なのが、縮尺、緯度、経度ごとに地図の画像を用意して、それをつなぎ合わせて表示する、という方法。国土地理院のサイトでわかりやすく説明されていますので詳細はそちらを参照ください。
地理院地図 | 地理院タイル仕様

上記リンク先で図示されているような形でズームレベルごとのタイル分割してみると、こんな感じになります。

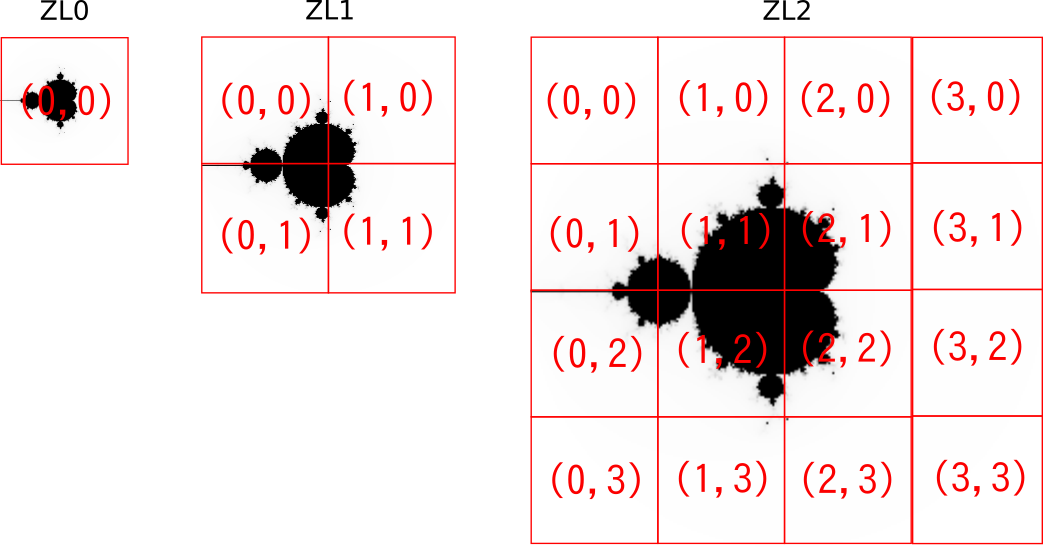
一般的にタイル1枚の画像のサイズは256x256ピクセルにします。(Retina用だと512x512ピクセルとかを使うこともあるようです)

この画像を{z}/{x}/{y}.pngというパスに配置します。(zはズームレベル、x,yはそのズームレベルでの画像の位置)

Leaflet

詳細はLeafletのサイトを参照のこと。

日本語での説明は、Wikipediaによると

Leaflet は広く使われているWeb地図のためのJavaScriptライブラリである。 2011年に最初にリリースされた。 モバイルとデスクトップのプラットフォームのほとんどに対応し、HTML5とCSS3に対応している。 OpenLayersやGoogle Maps API（英語版）とともに最も人気のあるJavaScript地図ライブラリの一つであり、FourSquare、Pinterest、Flickrなどの有名なサイトで使われている。

ということになります。
上記のようなタイル画像を使ってWeb上で地図表示をするのによく使われています。(地理院タイルを使って地図表示とかも簡単)

地図表示用に使われるLeafletを今回のように地図でない画像表示に使う方法に関しては、この記事の続きで記載したいと思います。

マンデルブロ集合のタイル画像の作成

で、マンデルブロ集合のタイル画像の作成に関してです。

-2-2i〜2+2iの範囲をズームレベル0で描画するとすると、-2〜2の4の範囲を256分割で計算するわけなので、1ピクセルあたり4/256=1/64単位で計算することになります。
ズームレベル1だとタイル1枚あたり、2の範囲を256分割になりますので、1ピクセルあたり2/256=1/128、ズームレベル2だと1/256…という形で計算単位を細かくしていきます。

実際にPythonで計算してPNGに保存するソースはこちら。githubにもおいてあります。

mandelbrot.py

"""マンデルブロ集合を描画する."""
from argparse import ArgumentParser
from itertools import product
from os import makedirs, path

import numpy
from PIL import Image
from tqdm import tqdm


def main():
    """メイン関数."""
    parser = ArgumentParser()
    parser.add_argument('outdir')
    parser.add_argument('level', type=int)
    args = parser.parse_args()
    outpath = path.join(args.outdir, str(args.level))
    tile_num = 2 ** args.level
    tile_wid = 4.0 / tile_num

    lefttop = -2.0+2.0j
    delta = tile_wid / 256

    xylist = list(product(range(tile_num), range(tile_num)))
    for x, y in tqdm(xylist):
        img = get_image(lefttop + x * tile_wid - (y * tile_wid) * 1j, delta)
        outpath = path.join(args.outdir, str(args.level), str(x))
        makedirs(outpath, exist_ok=True)
        imgname = path.join(outpath, f'{y}.png')
        img.save(imgname)


def get_image(lefttop, delta):
    """マンデルブロ集合のpillowイメージを取得する

    Arguments:
        lefttop {complex} -- 左上
        delta {float} -- 1pxの差

    Returns:
        Image -- 作成したイメージ
    """
    imgarray = numpy.zeros((256, 256), dtype=numpy.uint8)

    for rstep, istep in product(range(256), range(256)):
        c = lefttop + rstep * delta - (istep * delta) * 1j
        z = 0
        for i in range(256):
            z = z ** 2 + c
            if abs(z) > 2:
                imgarray[istep][rstep] = 255 - i
                break

    img = Image.fromarray(imgarray)
    return img


if __name__ == "__main__":
    main()

1ピクセルごと愚直に計算する処理にしてます。

python mandelbrot.py docs/tiles/grayscale 2

とすることで、ズームレベル2のタイルをdocs/tiles/grayscaleディレクトリの下に出力する…という動作になります。

最後に

まずはタイル画像の生成までをこの記事に書きました。
そのタイル画像をLeafletを使って実際に表示するところに関しては続きの記事に記載したいと思います。
↓
続きを書きました。