情報ボトルネックを超深掘りする話 - なぜ3x3は成功し、7x7は失敗したのか
前回(13日目 auto-encoderで自前のモデルを作る話2)、512x512への解像度拡大で予想外の問題に直面しました。
再構成(Reconstruction)は問題なく動作するのに、FaceSwap(デコーダ交換)が完全に失敗する。損失値は順調に下がっているのに、肝心の目的が達成されない。
その原因は、ボトルネックが3x3から7x7に拡大したことでした。
しかし、なぜボトルネックのサイズが、これほど決定的な影響を与えるのでしょうか?
今回は、この問いに対して、情報理論の観点から厳密な答えを探ります。
${\tiny \textsf{ここから先は今回、少しややこしい話が続きますができるだけ噛み砕いて説明します。なので少し冗長です、すいません。}}$
${\tiny \textsf{「つまり」も多いし・・・}}$
機械学習って理屈や理由がなくても、『たくさん問題と正解を見せれば新たな問題でも解ける』 が一つの大きなアドバンテージなんですが、今回はあえて理屈や理由を探ろうって話になります。
0. 前回までのおさらい
12日目 auto-encoderで自前のモデルを作る話1: 256x256-3x3で成功
結果:
• 再構成:成功(高品質)
• FaceSwap:**成功**(srcのポーズ・表情 + dstのidentity)
• 圧縮率:21.3倍(約4.7%)
13日目: 512x512-7x7で失敗
結果:
• 再構成:成功(それなりに高品質)
• FaceSwap:**失敗** (入力画像のindentityをかなりひきづってる)
• 圧縮率:15.7倍(約6.4%)
今回の問い
「なぜ、9個の空間グリッド(3x3)では成功し、49個(7x7)では失敗するのか?」
これは単なる経験則ではなく情報理論に基づいた厳密な説明が可能です。
1. Information Bottleneck Method - 情報ボトルネック法
1.1 背景:情報の「意味」とは何か
シャノンの情報理論(1948)は、情報の「伝送」に焦点を当てました。しかし、「受信者にとっての情報の価値」や「意味」については、意図的に除外されていました。
シャノンは「封筒」を汚さず届ける技術を確立しましたが、現代の機械学習は「中身(意味)」の抽出へと進化しました。
例えば、音声認識を考えてみましょう:
- 音声データ $X$: 波形、ノイズ、声色、アクセント、背景音、すべてが含まれる
- 本当に必要な情報: 話された「単語」だけ
しかし、「単語を認識する」という目的がなければ、何が「ノイズ」で何が「信号」かを定義できません。
Naftali Tishby らは2000年、この問題に対して Information Bottleneck Method(情報ボトルネック法)を提案しました。
論文: Tishby, N., Pereira, F. C., & Bialek, W. (2000). The information bottleneck method. arXiv preprint physics/0004057.
https://arxiv.org/abs/physics/0004057
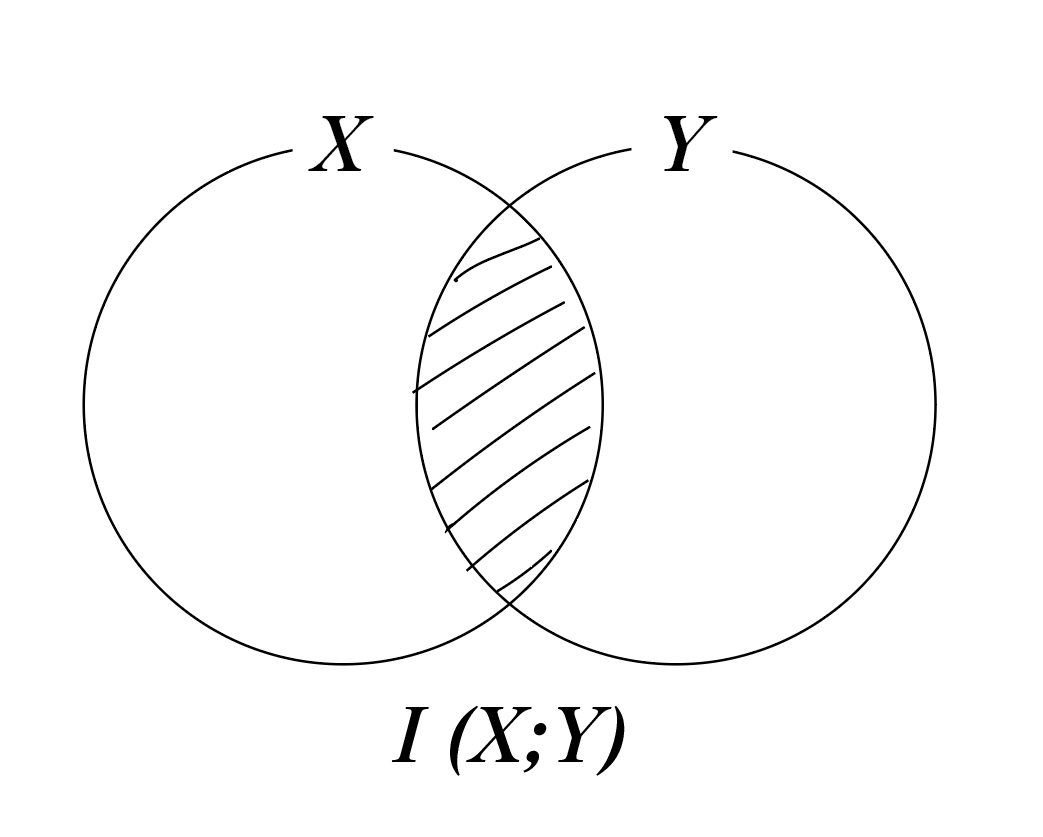
1.2 相互情報量 I(X;Y) - 情報理論の基礎
まず、相互情報量(Mutual Information)を理解する必要があります。
定義:
$$I(X;Y) = \sum_{x,y} p(x,y) \log \frac{p(x,y)}{p(x)p(y)}$$
直感的な意味:
「変数 $X$ を知ったとき、変数 $Y$ についての不確実性がどれだけ減るか」
->すごく雑にいうと、 XとYが最初から被ってる部分です。
- $I(X;Y) = 0$: $X$ と $Y$ は完全に独立(一方を知っても、他方について何も分からない)
- $I(X;Y)$ が大きい: $X$ と $Y$ は強く関連(一方を知れば、他方もかなり分かる)
重要な性質:
$$I(X;Y) = H(Y) - H(Y|X)$$
- $H(Y)$: $Y$ のエントロピー(不確実性)
- $H(Y|X)$: $X$ を知った後の $Y$ の条件付きエントロピー
- つまり、相互情報量 = 不確実性の減少量
さらにかみ砕くと、
• 得られた情報量 =(元のわからなさ)−(ヒントをもらった後のわからなさ)
H(Y)=100 (初期エントロピー) 最初、どこにあるか全くわからなくて、探さないといけない場所が100個ある状態。「うわ、先が長いな…」という不確実性の大きさ。
H(Y∣X)=5 (条件付きエントロピー) ヒント(X)を使って調べた結果、まだ確定できずに残ってしまった怪しい場所が5個。「まだここだけは分からないな」という残りの不確実性。
I(X;Y)=95 (相互情報量) ヒント(X)のおかげで、「ここはもう探さなくていい(確定した)」と潰せた場所が95個。「95個分も楽になったぞ!」という情報の利得。
つまり結論
「情報量(I)とは、『わかったこと(事実)』そのものの量ではなく、『それによって消えた選択肢(徒労)』の量である」
なぜセミコロン(;)?
相互情報量では、慣習的に $I(X;Y)$ とセミコロンを使います。これは、同時確率 $p(X,Y)$ や結合エントロピー $H(X,Y)$ のカンマ表記と区別するためです。
1.3 情報ボトルネック法の定式化
Tishbyらは、「関連情報(Relevant Information)」を以下のように定義しました:
設定:
- $X$: 入力信号(例:音声波形、顔画像)
- $Y$: 予測したいターゲット(例:単語、再構成画像)
- $\tilde{X}$: 圧縮された表現(ボトルネック)
目的:
$X$ の情報を圧縮した表現 $\tilde{X}$ を作成する際、以下の2つの相反する目的をバランスさせる:
- 圧縮: $X$ から $\tilde{X}$ への情報量を最小化 → $I(\tilde{X};X)$ を小さく
- 保存: $\tilde{X}$ が $Y$ について持つ情報を最大化 → $I(\tilde{X};Y)$ を大きく
**変分原理**:
これは、以下の汎関数 $\mathcal{L}$ を最小化する変分問題として定式化されます:
$$\mathcal{L}[p(\tilde{x}|x)] = I(\tilde{X};X) - \beta I(\tilde{X};Y)$$
各項の意味:
-
第1項 $I(\tilde{X};X)$: 入力 $X$ と圧縮表現 $\tilde{X}$ の相互情報量
- この項を最小化したい(圧縮率を上げる)
-
第2項 $-\beta I(\tilde{X};Y)$: ターゲット $Y$ と圧縮表現 $\tilde{X}$ の相互情報量(マイナス符号付き)
- $\mathcal{L}$ 全体を最小化するため、この項は最大化される
- つまり、$Y$ に関する情報は保持したい
-
パラメータ $\beta$: ラグランジュ乗数
- 圧縮と保存のトレードオフを調整
- $\beta$ を変化させることで、情報の「解像度」を探索できる
冗長になるが、言い換えると、
この式は、「あちらを立てればこちらが立たず」という2つの願いを、1つの式で無理やり解決しようとするものです。
マイナスがついているので、全体(損失 $\mathcal{L}$)を小さく(最小化)するには、
「元の数(第一項)」を圧縮して「引く数(第二項)」をできるだけデカくすればいいわけです。
1. 第一項: $I(\tilde{X};X)$ を小さくしたい
- 「忘れろ!捨てろ!」
- 役割: 入力データ $X$ (ノイズまみれの元データ)との関係を断ち切りたい。つまり、情報を可能な限り圧縮(忘却)したいのです。
- ここが小さいと: データがスリムになり、余計なノイズが消えます(汎化性能が上がる)。
2. 第二項:$I(\tilde{X};Y)$ を大きくしたい
- 「でも、大事なことだけは覚えておけ!」
- 役割: 正解 $Y$ (タスクの答え)についての情報はガッチリ持っておきたい。
- ここが大きいと: 予測の正解率が上がります。
つまり、「カンニングペーパー」作りです
この数式は、テストのためにカンニングペーパー($\tilde{X}$)を作る作業に例えられます。
-
第一項を小さく(圧縮):
先生に見つからないように、ペーパーは 「極限まで小さく」 しなきゃいけない。教科書($X$)を丸写ししたらバレる(過学習する)。 -
第二項を大きく(精度):
でも、テスト($Y$)で**「満点を取れる内容」**じゃなきゃ意味がない。
結論:
「紙は最小限のサイズにしろ(第一項)。でも、答えは全部書け(第二項)。」
という、ワガママな命令を $\beta$ でバランス調整しているのがこの式です。
この図のように、$\beta$ を変えることで、「精度重視(紙が大きくてもいい)」か「圧縮重視(とにかく小さく)」かのバランスが決まります。
重要な洞察:
この定式化では、「何が重要な特徴か(歪み尺度)」を事前に定義していません。
かつてのRate-Distortion理論では、歪み関数 $d(x, \tilde{x})$ を人間が定義する必要がありました。しかし、情報ボトルネック法では、変分原理の結果として カルバック・ライブラー情報量($D_{KL}$)が自然に「有効な歪み尺度」として導出されます。
1. $d(x, \tilde{x})$ って何?
これは**「コピーの劣化具合を測る定規」**のことです。
x: オリジナルの高画質画像
$\tilde{x}$ : 圧縮した汚い画像
d(Distortion): 「どれくらい似てないか」のスコア(歪み)
昔の理論(Rate-Distortion)では、この定規を人間が最初に決める必要がありました。
• 「色の差を測る?」
• 「輪郭のボケを測る?」
• 「ピクセルのズレを測る?」
人間が「ズレはこうやって測りなさい」と数式(d)で指定してあげないと、圧縮ができなかったのです。
2. 何が問題だったの?
「意味」が測れないことです。
例えば、**「猫の画像」**を圧縮する場合:
人間が決めた定規(ピクセルの差): 「背景の壁紙の模様がボヤけてしまった! d(劣化スコア)が高い! これは悪い圧縮だ!」
でも実際は、
本当にやりたいこと(意味): 「いや、猫さえ綺麗に写っていれば、背景なんてボヤけててもいいんだよ…」
人間が決めた物理的な定規(d)では、「どっちのズレが致命的で、どっちのズレはどうでもいいか」までは判断できなかったのです。
3. IB理論のすごいところ:「定規」が勝手に生えてくる
IB理論では、人間は「定規(d)」を渡しません。 その代わりに、
「ターゲット(Y=猫かどうか)を当てろ」
という命令だけを与えます。
すると、数式を解いていく過程で、「カルバック・ライブラー情報量(D KL)」という数学的なパーツが勝手に出現します。
これが、「新しい定規」 の正体です。
昔の定規(d): ピクセルがどれだけズレたか測る(物理的)
勝手に出てきた定規(D KL): 「猫だと判定する確率」がどれだけズレたか測る(意味的)
つまり、
昔は『画像の劣化とはピクセルのズレである』と人間が定義してやる必要があった(d)。
でもIB理論では、『目的(Y)の役に立つか?』という観点だけで計算を進めると、
『確率のズレ(D KL)こそが真の劣化尺度だ!』という結論が、計算結果として自然に湧いて出てきます。
→ 「人間が採点基準を作らなくても、タスク自身が最適な採点基準(定規)を生み出すのです。
「何が重要か」はデータとタスク($Y$ の定義)から 創発(emerge) するのです。
->あぶり出されるということです。
1.4 AutoEncoderとの対応
通常の教師あり学習では、$Y$ は明確なラベル(例:「猫」「犬」)です。
しかし、**AutoEncoder(自己符号化器)**の場合:
$$Y = X$$
つまり、「入力と同じものを出力する」タスクです。
情報ボトルネックの解釈:
- 目標: 右辺の $X$(ターゲット)を再構成したい
- 制約: ボトルネック $\tilde{X}$ の容量が限られている
- 結果: $X$ の中で「再構成に最も重要な情報」だけが $\tilde{X}$ に残る
これは、まさに**「潜在空間でのデノイズ(ノイズ除去)」**です。
ボトルネックが狭ければ狭いほど、「どうしても必要な情報」と「あってもなくてもいい情報」の選別が厳しくなります。
L1 Lossとの関係:
機械学習では、L1 Lossやクロスエントロピー誤差を最小化します。これは、$I(\tilde{X};Y)$ を最大化することと深く関連しています。
• L1 Loss最小化 ≈ ピクセルレベルでの Y の予測精度を上げる
• LPIPS Loss最小化 ≈ 知覚的な Y の予測精度を上げる
つまり、通常の損失関数は、情報ボトルネック法の第2項($I(\tilde{X};Y)$ の最大化)に対応します。
一方、第1項($I(\tilde{X};X)$ の最小化)は、明示的な損失関数ではなく、**アーキテクチャ(ボトルネックの物理的な狭さ)**によって実現されているのです。
2. FaceSwapへの適用
2.1 変数の対応関係
FaceSwapのAutoEncoderにおいて、情報ボトルネック法の変数を対応付けると:
| 論文の変数 | FaceSwapでの意味 | 具体例 |
|---|---|---|
| $X$ | 入力画像 | src画像、dst画像 |
| $Y$ | 再構成ターゲット | 同じ画像($Y=X$) |
| $\tilde{X}$ | ボトルネック表現 | (1024, 3, 3) または (1024, 7, 7) |
重要な追加要素:
FaceSwapでは、$X$ に含まれる情報をさらに分解できます:
• Identity(アイデンティティ): 「誰の顔か」(二重まぶた、顔の形、メガネなど)
• Pose/Expression(ポーズ・表情): 「どんな表情・角度か」(笑顔、右向き、目を閉じているなど)
FaceSwapの目的:
- $\tilde{X}$ には Pose/Expression のみを保存したい
- Identity は捨てたい(Decoderが付与する)
この「選別」が、ボトルネックによって自動的に行われることを期待しています。
2.2 3x3成功の理論的説明
256x256-3x3のケース:
$$
\begin{align}
&\text{入力}: \quad 256 \times 256 \times 3 = 196,608 \text{ 個の値} \
\end{align}
$$
$$
\begin{align}
&\text{ボトルネック}: \quad 3 \times 3 \times 1024 = 9,216 \text{ 個の値} \
\end{align}
$$
$$
\begin{align}
&\text{圧縮率}: \quad 196,608 / 9,216 = 21.3 \text{倍}
\end{align}
$$
情報ボトルネックの観点:
目的関数を再掲します:
$$\mathcal{L} = I(\tilde{X};X) - \beta I(\tilde{X};Y)$$
3x3のボトルネックでは、第1項 $I(\tilde{X};X)$ が物理的に制限(圧縮)されます。
容量が極小(9,216個)のため、$X$ の全情報を $\tilde{X}$ にコピーすることは不可能です。
モデルの判断:
目的関数 $\mathcal{L}$ を最小化するため、モデルは以下のように考えます:
- 第2項を最大化したい($I(\tilde{X};Y)$ を大きく)= 再構成品質を上げたい
- しかし、第1項の制約(容量不足)により、全情報は入らない
- では、「再構成に最もコスパの良い情報」だけを選ぼう
Pose vs Identityの優先順位:
- Poseを捨てる: 顔の向き、表情が変わると、全ピクセルが大幅に変化 → L1 Loss爆発
- Identityを捨てる: 二重まぶたが一重になっても、ポーズが合っていればピクセル誤差は小さい
つまり、L1 Lossへの寄与度では:
$$\text{Pose/Expression} \gg \text{Identity}$$
結果:
容量制限により、モデルは「仕方なく」Identityを捨て、Pose/Expressionを優先します。
そして、Decoder自身が特定人物のIdentityを学習しているため、$\tilde{X}$(Poseのみ)から元の画像を再構成できます。
これが、3x3ボトルネックによるIdentity分離の創発です。
2.3 7x7失敗の理論的説明
512x512-7x7のケース:
$$
\begin{align}
&\text{入力}: \quad 512 \times 512 \times 3 = 786,432 \text{ 個の値} \
\end{align}
$$
$$
\begin{align}
&\text{ボトルネック}: \quad 7 \times 7 \times 1024 = 50,176 \text{ 個の値} \
\end{align}
$$
$$
\begin{align}
&\text{圧縮率}: \quad 786,432 / 50,176 = 15.7 \text{倍}
\end{align}
$$
一見、圧縮率(15.7倍)は3x3の場合(21.3倍)と近いように見えます。
しかし、絶対的な容量が問題です。
情報ボトルネックの観点:
7x7では、$I(\tilde{X};X)$ に余裕があります。
50,176個の値があれば、Pose/Expression だけでなく、Identityも載せられます。
モデルの判断:
- 第2項を最大化したい($I(\tilde{X};Y)$ を大きく)= 再構成品質を上げたい
- 第1項の制約は緩い(容量に余裕)
- では、Identityも載せよう(その方がL1 Lossが下がる)
**なぜIdentityを載せるとLossが下がるのか?**
AutoEncoderでは $Y = X$ です。つまり、右辺の $X$(自分自身)を正確に再構成することが目標です。
- Identity情報がある場合: Decoderは「この顔は二重まぶただ」という情報を $\tilde{X}$ から得て、正確に再構成できる → L1 Loss小
- Identity情報がない場合: Decoderは「デフォルトのまぶた」を出力するしかない → L1 Loss大
つまり、L1 Lossを最小化するという観点では、Identityを $\tilde{X}$ に保存することは最適化的に正しいのです。タスク達成の近道であり、タスクそのものが容易になります。
Statistical Latent L2も無力:
12日目で導入した Statistical Latent L2 Loss:
\mathcal{L}_{\text{latent}} = \text{MSE}(\text{mean}(z_{\text{src}}), \text{mean}(z_{\text{dst}})) + \text{MSE}(\text{var}(z_{\text{src}}), \text{var}(z_{\text{dst}}))
これは、srcとdstの潜在分布の**統計量(平均・分散)**を近づけます。
7x7でも、この損失値は下がります。つまり、統計的には分布が近いのです。
しかし、問題は空間位置ごとの情報です。
例えば、7x7の空間グリッドの特定位置(例:左上)に、「この人はメガネをかけている」という情報を載せることができます。srcとdstで異なる情報を異なる空間位置に載せても、バッチ全体の平均・分散は近くなり得ます。
つまり、Latent L2は「統計的な類似性」を保証しますが、「各空間位置にIdentityを載せない」ことは保証しないのです。
結果:
容量に余裕があるため、モデルはIdentityを $\tilde{X}$ に保存します。
結果として、decoder_dst(encoder(src)) を実行しても、$\tilde{X}$ に含まれるsrcのIdentity情報が残り、FaceSwapが失敗します。
2.4 圧縮率だけでは説明できない
| 解像度 | ボトルネック | 入力要素数 | ボトルネック要素数 | 圧縮率 | 空間グリッド数 |
|---|---|---|---|---|---|
| 256x256 | 3x3 | 196,608 | 9,216 | 21.3倍 (4.69%) | 9 |
| 512x512 | 7x7 | 786,432 | 50,176 | 15.7倍 (6.38%) | 49 |
圧縮率だけ見ると、7x7の方がむしろ厳しいように見えます(15.7倍 vs 21.3倍)。
しかし、決定的な違いは空間グリッド数です。
- 3x3 = 9個: 「左上」「中央」「右下」のような、極めて粗い空間構造
- 7x7 = 49個: 「左目」「右目」「鼻」「口」「輪郭」といった、顔のパーツを個別に記述可能
モザイクで考える:
画像を3x3のモザイクにすると、個人を特定するのは困難です(誰だか分からない)。
しかし、7x7のモザイクなら、「目の大きさ」「口の形」などがぼんやりと見え、知っている人なら「誰だか分かる」状態になります。
この「ぼんやりと残ったIdentity情報」を、Encoderは1024チャンネルに圧縮して $\tilde{X}$ に詰め込み、Decoderで超解像することで、元のIdentityを復元できてしまうのです。
つまり、重要なのは:
「圧縮率(総要素数の比)」ではなく、「空間構造の絶対的な解像度」
3. 相転移(Phase Transition)としてのボトルネック拡大
3.1 相転移の概念
Tishbyらの論文では、情報の「解像度」(パラメータ $\beta$)を変化させると、保持される情報の質が不連続に変化する現象が論じられています。
"These transitions, in turn, form a hierarchy of relevantly quantized relevant information, at different resolutions."
(これらの遷移は、異なる解像度における関連情報の量子化の階層を形成する)
"...the solution curves bifurcate at certain finite values of $\beta$, and form second order phase transitions."
(解の曲線は特定の有限な $\beta$ 値で分岐し、二次相転移を形成する)
物理学の相転移とのアナロジー:
• 水を冷やしていくと、ある温度(0°C)で突然、液体から固体(氷)に変わる
• 温度を少し下げるだけで、性質が**質的に変化**する
情報ボトルネックでも同様に、ボトルネックの容量(または $\beta$)を変化させると、ある閾値で保持される情報の性質が激変します。
連続的変化 vs 不連続な変化:
• 連続的: ボトルネックを少し広げると、情報が「少しだけ増える」
• 不連続: ある閾値を超えた瞬間、保持される情報の 種類 が変わる
3x3 → 7x7は、後者の「相転移」に該当します。
3.2 3x3 → 7x7は相転移
空間グリッド数の変化:
$$3 \times 3 = 9 \quad \to \quad 7 \times 7 = 49 \quad (\text{約5.4倍})$$
これは単なる「5.4倍の増加」ではありません。
質的な変化:
| ボトルネック | 保持される情報 | FaceSwapの結果 |
|---|---|---|
| 3x3 (9個) | Pose/Expression のみ | 成功(Identity分離) |
| 7x7 (49個) | Pose/Expression + Identity | 失敗(Identity混入) |
フェーズ(相)の転移:
- 3x3のフェーズ: 「構造のみ保持可能」状態
- 7x7のフェーズ: 「個体差も保持可能」状態
ある閾値(おそらく16〜36個の間)を超えた瞬間に、システムの質的特性が切り替わってしまったのです。

${\tiny \textsf{左から元画像、3x3、7x7}}$
3.3 (たぶん)6x6でも失敗する理由
「じゃあ、512x512の入力で、ボトルネックを6x6にしたら?」
という疑問が湧くかもしれません。512x512の場合、256x256との入力解像度の比は2倍なので、ボトルネックも2倍(3x3 → 6x6)にすれば「比率」は維持されます。
しかし、6x6でもFaceSwapは失敗する可能性が極めて高いです。
理由:「比率」ではなく「絶対数」の問題
$$6 \times 6 = 36 \text{ 個の空間グリッド}$$
36個あれば、以下のような空間的な記述が可能です:
- 左目(6個のグリッド)
- 右目(6個のグリッド)
- 鼻(4個のグリッド)
- 口(8個のグリッド)
- 輪郭・その他(12個のグリッド)
これだけあれば、「目の形(二重/一重)」「口の大きさ」といったIdentity情報を、各領域のチャンネル(1024次元)に埋め込むことができます。
臨界点の推定:
相転移の閾値は、おそらく以下の範囲にあると考えられます:
- 9個(3x3): Identity保持不可能 → FaceSwap成功
- 16個(4x4): ギリギリのライン?(未検証)
- 36個(6x6): Identity保持可能 → FaceSwap失敗
- 49個(7x7): Identity保持容易 → FaceSwap失敗
モデルは「比率が維持されているからIdentityを捨てよう」とは考えません。「36個も空きがあるなら、Lossを下げるためにIdentityを全部詰め込もう」と判断します。
これがL1最小化の引力です。
4. もし7x7で成功させるなら? - ソフトな制約の導入
4.1 ハード制約 vs ソフト制約
3x3と7x7の違いを、制約の種類で整理できます:
| ボトルネック | 制約の種類 | Identity排除の仕組み |
|---|---|---|
| 3x3 |
Hardware Constraint (物理的制約) |
容量が足りず、物理的に通れない |
| 7x7 | (制約なし) | だだ漏れ |
| 7x7 + 追加Loss |
Software Constraint (損失関数による制約) |
通ろうとすると罰される |
3x3の成功は、アーキテクチャ自体が制約を課していることによります。
一方、7x7で成功させるには、損失関数(目的関数 $\mathcal{L}$)を改変し、「広い通路を通り抜けようとするIdentity情報を検知して罰する」必要があります。
情報ボトルネック法の式で言えば:
$$\mathcal{L} = I(\tilde{X};X) - \beta I(\tilde{X};Y)$$
7x7では第1項($I(\tilde{X};X)$)の圧力が弱いため、新たな項を追加する必要があります。
例えば:
\mathcal{L}_{\text{new}} = I(\tilde{X};X) - \beta I(\tilde{X};Y) + \gamma I(\tilde{X};Z_{\text{id}})
ここで $Z_{\text{id}}$ はIdentity変数、$\gamma$ はペナルティの重みです。
つまり、$I(\tilde{X};Z_{\text{id}})$ は、$\tilde{X}$ に含まれる $Z$ アイデンティティです。
4.2 Approach 1: Adversarial Identity Loss(敵対的Identity消去)
基本アイデア:
「EncoderがIdentityを通過させたら、Discriminatorが検知して罰する」
実装:
# Discriminator: ボトルネックを見て、srcかdstかを分類
identity_pred = discriminator(z) # zは(1024, 7, 7)
# Encoderの目的: Discriminatorを騙す(分類できないようにする)
loss_adversarial = -log(p(src)) - log(p(dst)) # 均等分布を目指す
# 全体の損失
loss = loss_l1 + loss_lpips + loss_kl + gamma * loss_adversarial
情報理論的解釈:
$$I(\tilde{X}; Z_{\text{id}}) \to 0$$
つまり、ボトルネック表現 $\tilde{X}$ とIdentity変数 $Z_{\text{id}}$ の相互情報量を最小化します。
効果:
Encoderは、「7x7の広さはあるけれど、そこにIdentity情報を書くとDiscriminatorに見つかって怒られる。だから、Pose/Expressionだけを書こう」と学習します。
欠点:
- Discriminatorの学習が不安定(GAN系の既知の問題)
- ハイパーパラメータ $\gamma$ の調整が難しい
- 訓練が複雑化
4.3 Approach 2: ID Loss(ArcFace / CosFace)
基本アイデア:
「FaceSwapの結果が、期待する人物(dst)に見えなければ罰する」
実装:
# FaceSwapを実行
swap_result = decoder_dst(encoder(src))
# 事前学習済みの顔認証モデル(ArcFace)で特徴抽出
feat_result = arcface(swap_result)
feat_dst = arcface(dst)
# ID Loss: コサイン類似度を最大化
loss_id = 1 - cosine_similarity(feat_result, feat_dst)
# 全体の損失
loss = loss_l1 + loss_lpips + loss_kl + gamma * loss_id
効果:
もし7x7のボトルネックを通ってsrcのIdentityが漏れていたら、swap_result はsrcに似てしまいます。
すると、feat_result と feat_dst の類似度が下がり、Lossが跳ね上がります。
モデルはLossを下げるために、**「EncoderがIdentityを送らないようにする」**ことを強制されます。
利点:
- 事前学習済みモデル(ArcFace)が利用可能
- 明確な目的(「dstに見える」)
- DeepFake系モデル(SimSwapなど)で実績あり
欠点:
- 外部モデル(ArcFace)への依存
- 訓練データがArcFaceの訓練分布と異なる場合、効果が薄い可能性
4.4 Approach 3: Landmark / Structure Loss(幾何学的制約)
基本アイデア:
「ピクセル一致(L1)を諦め、構造の一致を目指す」
Day 13の失敗原因は「L1 Lossを下げるためにIdentityを通過させた」ことでした。
ならば、L1 Lossの支配力を弱める必要があります。
実装:
# 顔ランドマーク(目・鼻・口の座標)を抽出
landmarks_input = landmark_detector(input)
landmarks_output = landmark_detector(output)
# 幾何学的な一致のみを要求
loss_landmark = mse(landmarks_input, landmarks_output)
# L1の代わりに、ランドマークを主損失に
loss = gamma * loss_l1 + loss_landmark + loss_lpips
情報理論的解釈:
「関連情報 $Y$」の定義を書き換えます:
- Before: $Y =$ ピクセル値そのもの(Identity含む)
- After: $Y =$ 幾何学的な配置情報(Pose/Expressionのみ)
効果:
モデルは「目がここにあればいい」「口が開いていればいい」と判断し、テクスチャや微細な形状(Identity)を7x7に載せる動機を失います。
利点:
- L1の「ピクセル完全一致」という罠を回避
- タスク(FaceSwap)の本質に合致
欠点:
- ランドマーク検出器が必要
- テクスチャの品質が下がる可能性
4.5 思考実験のまとめ
上記3つのアプローチは、すべて目的関数 $\mathcal{L}$ の改変です。
| アプローチ | 追加する項 | 効果 |
|---|---|---|
| Adversarial | $+\gamma I(\tilde{X};Z_{\text{id}})$ | Identity情報にペナルティ |
| ID Loss | $+\gamma (1 - \cos(\text{ArcFace}(\text{swap}), \text{ArcFace}(\text{dst})))$ | Swap結果がdstに見えることを強制 |
| Landmark | L1を減らし、幾何学的損失を増やす | $Y$ の定義を変更 |
いずれも、「7x7という広い通路を、無理やり使わせないようにする」アプローチです。
3x3における本質的な見通しの良さ:
対照的に、3x3はこれら複雑な損失関数なしで、Identity分離が創発しました。
物理的な制約だけで、モデルが「正しい選択」をするように誘導できたのです。
これが、3x3という設計のエレガントさです。
5. 設計哲学としての情報ボトルネック
5.1 「大は小を兼ねない」
一般的に、機械学習では「モデルは大きければ大きいほど良い」と考えがちです。
• より多くのパラメータ
• より深い層
• より広い中間層
しかし、情報ボトルネックの文脈では、「狭すぎるボトルネック」が必要な場合があります。
FaceSwapにおいて:
• 7x7: 容量が大きい → Identity保持 → 失敗
• 3x3: 容量が小さい → Identity捨象 → 成功
「大は小を兼ねない」 のです。
タスクに応じた「適切な狭さ」を見つけることが、設計の鍵となります。
5.2 損失関数 vs アーキテクチャ
機械学習の設計要素は、大きく2つに分けられます:
- 損失関数: 「何を学習するか」を定義
- アーキテクチャ: 「何が学習可能か」の制約を定義
従来、多くの研究は損失関数の工夫に焦点を当ててきました:
• L1 → L2 → Perceptual Loss → Adversarial Loss
• 重み調整、スケジューリング、新しい正則化項
しかし、3x3ボトルネックは、アーキテクチャ(構造)自体が問題を解いた例です。
損失関数だけでは解けない問題:
7x7のケースで見たように、通常の損失関数(L1, LPIPS, Latent L2)では、Identity分離を強制できませんでした。
「L1 Lossを下げる」という目的と、「Identityを捨てる」という目的が、根本的に矛盾していたからです。
一方、3x3という物理的制約は、この矛盾を強制的に解消しました。
設計の優先順位:
- まず、タスクに適した**アーキテクチャ(情報の流れ、ボトルネック)**を設計
- その上で、損失関数で微調整
この順序が重要です。
5.3 創発(Emergence)
創発とは、個々の要素には存在しない性質が、システム全体として現れる現象です。
3x3ボトルネックにおけるIdentity分離は、まさに創発です:
• 明示的に教えていない: 損失関数に「Identityを捨てろ」という項はない
• しかし実現する: 物理的制約(ボトルネックの狭さ)と、損失関数(L1最小化)の組み合わせが、「Identity捨象」を生む
情報ボトルネック法の理論は、この創発が偶然ではなく必然であることを示しています。
$$\mathcal{L} = I(\tilde{X};X) - \beta I(\tilde{X};Y)$$
第1項の物理的制約が十分に強ければ、第2項の最適化過程で、「意味のある特徴」だけが自然に選ばれるのです。
6. まとめ
1. Information Bottleneck Methodは、FaceSwapの成功/失敗を説明する
目的関数:
$$\mathcal{L} = I(\tilde{X};X) - \beta I(\tilde{X};Y)$$
• 3x3: 第1項(圧縮)が支配的 → Identity捨象
• 7x7: 第2項(再構成)が支配的 → Identity保持
2. 3x3と7x7の違いは「相転移」
• 単なる量的変化ではなく、質的変化
• ある閾値(9〜36個の間)を超えると、保持される情報の性質が激変
• 6x6でも失敗する理由:絶対数が閾値を超えている
3. ボトルネック設計は機械学習の核心
• 損失関数だけでは解けない問題がある
• アーキテクチャ(物理的制約)が本質的
• 「大は小を兼ねない」
4. 7x7でも成功させる方法は存在する(理論上)
• Adversarial Identity Loss
• ID Loss (ArcFace)
• Landmark / Structure Loss
しかし、いずれも 複雑な調整が必要。 3x3の「損失関数なしで創発」というのがとてもシンプルに全てをまとめていたのではないか。
このような考察となりました。
参考文献:
- Tishby, N., Pereira, F. C., & Bialek, W. (2000). The information bottleneck method. arXiv preprint physics/0004057. https://arxiv.org/abs/physics/0004057
- Shannon, C. E. (1948). A mathematical theory of communication. Bell system technical journal, 27(3), 379-423.
- Cover, T. M., & Thomas, J. A. (2006). Elements of information theory. John Wiley & Sons.