行列積・内積について
数学の勉強をしていると、「内積」という単語が出てきました。
この「内積」がニューラルネットワークでどのように使われているか調べました。
なお、内積はベクトルについての積ですが、行列積は行列についての積です。
内積は、「ドット積」とも呼ぶようです。
内積とは
行列積とは
例
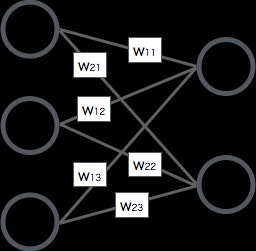
下記のような2層のニューラルネットワークを考えてみます。
行列積の式
上記のニュラールネットワークの出力を、行列積の式に置き換えると、こんな感じになります。
\begin{bmatrix}
w_{11} & w_{12} & w_{13}\\
w_{21} & w_{22} & w_{23}
\end{bmatrix}
\cdot
\begin{bmatrix}
x_{1} \\
x_{2} \\
x_{3} \\
\end{bmatrix}
手計算
具体的に数字を当てはめて
\begin{bmatrix}
1 & 2 & 3\\
4 & 5 & 6
\end{bmatrix}
\cdot
\begin{bmatrix}
1 \\
2 \\
3 \\
\end{bmatrix}
手計算すると
\begin{bmatrix}
1 \times 1 + 2 \times 2 + 3 \times 3 \\
4 \times 1 + 5 \times 2 + 6 \times 3 \\
\end{bmatrix}
=
\begin{bmatrix}
14 \\
32 \\
\end{bmatrix}
Numpyでは
import numpy as np
w = np.array([[1,2,3],[4,5,6]])
x = np.array([[1],[2],[3]])
w.dot(x) #=> array([[14],[32]])
w.dot(x)はwとxの行列積を表します。
ちなみに、「dot product(ドット積)」からdotというメソッド名になっています。
Tensorflowでは
import tensorflow as tf
w = tf.get_variable("weight" , initializer=tf.constant(np.array([[1,2,3],[4,5,6]]).astype("int32")))
x = tf.get_variable("x" , initializer=tf.constant(np.array([[1],[2],[3]]).astype("int32")))
セッション初期化
init = tf.initialize_all_variables()
sess = tf.Session()
sess.run(init)
sess.run(tf.matmul(w, x)) #=> array([[14],[32]])
tf.matmul(w, x)はwとxの行列積を表します。
ちなみに、「matrix multiplication(行列積)」からmatmulというメソッド名になっています。