目次
1. 目次
2. 記事の内容について
3. 本題
4. 参考
5. 所感
記事の内容
本記事はO'REILLYの『Scikit-LearnとTensorFlowによる実践機械学習』[1]を参考に、kaggleのHouse Prices: Advanced Regression Techniquesに挑戦した結果を記事にまとめたものです。
あくまで個人の学習記録です。
本題
細かい部分はgithubを見てください。こちら
流れは層化抽出法で分ける、量的変数の相関係数を出す、欠損値を補完する、質的変数の相関比を出す、欠損値を補完する、pipelineを用意する、モデルを用意する、学習を行う、誤差を検証する、テストセットを用意する、予測を行う、というものです。
データの概観
df = pd.read_csv('input/train.csv')
train_set, test_set = train_test_split(df, test_size=0.2, random_state=42)
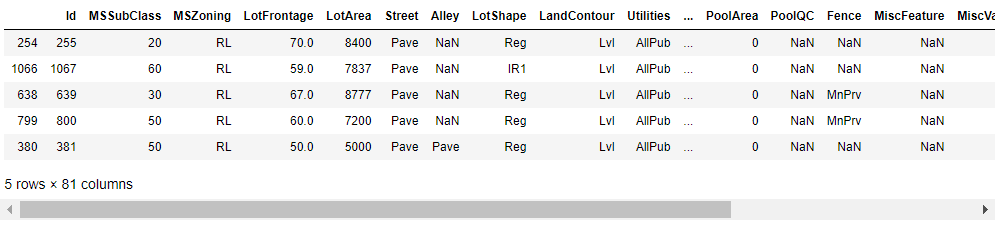
train_set.head()
IdとSalePriceを含めて81columnsあります。ひとつひとつの変数を見ていくのは骨が折れそうです。一説によると変数の数は多くても10個らしいのでどうにか絞らなくてはなりません。また、質的変数が多いのも厄介です。
層化抽出法
本にならって訓練用データから訓練セットとテストセットにデータを分けます。
一般的に建築年数と住宅価格に相関があると考えられるので年代ごとにデータを分けます。これはデータセットごとにバイアスができてしまうことを防ぐ意味があります。
# 適当な値で分割
df["YearBuilt_cat"] = pd.cut(df["YearBuilt"],
bins=[1870, 1920, 1940, 1960, 1980, 2000, np.inf],
labels=[1, 2, 3, 4, 5, 6])
# 層ごとに振り分ける
from sklearn.model_selection import StratifiedShuffleSplit
split = StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=42)
for train_index, test_index in split.split(df, df["YearBuilt_cat"]):
strat_train_set = df.loc[train_index]
strat_test_set = df.loc[test_index]
相関係数
sckit-leanでは簡単にcorr()メソッドで相関係数が求められます。
corr_matrix = df.corr()
corr_matrix["SalePrice"].sort_values(ascending=False)
今回は相関変数の大きい9つの変数を用います。
corr_index = corr_matrix["SalePrice"].sort_values(ascending=False).index
index_n = corr_index[0:10].values.tolist()
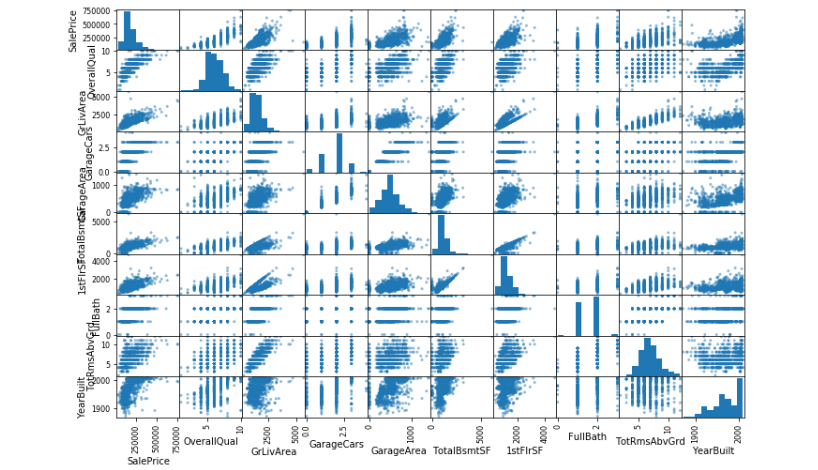
scatter_matrix(df[index_n], figsize=(12, 8))
SalePriceに関して基本的にはどの変数も正の相関がみられるので、今回はそのまま変数として扱います。
なお、seaborn等を用いて色分けをして図示したり、偏相関係数を求めて擬似相関を考えることもできますが、今回は無視します。
参考 偏相関係数と擬似相関
欠損値の補完
中央値を選択
from sklearn.impute import SimpleImputer # Scikit-Learn 0.20+
imputer = SimpleImputer(strategy="median")
df_num = df[index_n[1:]]
imputer.fit(df_num)
質的変数
df_cat = strat_train_set.drop(corr_index[1:].values.tolist(), axis=1)
df_cat = df_cat.drop('YearBuilt_cat', axis=1)
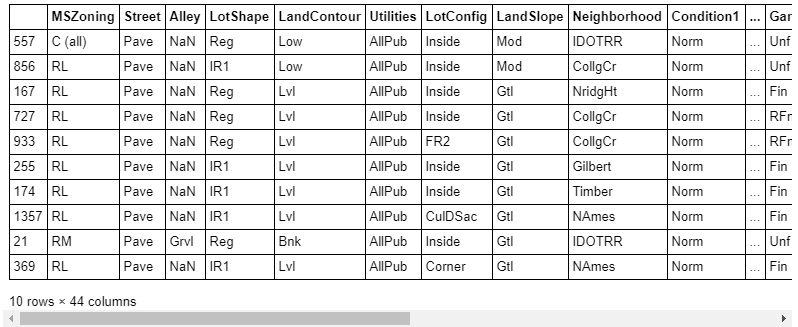
df_cat.head(10)
fig = plt.figure(figsize=(12,300))
for i in np.arange(43):
ax = fig.add_subplot(43,1,i+1)
sns.boxplot(x=df_cat.iloc[:,i], y=df_cat.SalePrice)
plt.show()
質的変数の相関比
箱ひげ図ではどの変数にどんな意味があるか分かりにくいので今回は相関比を求めます。scikit-learnでは質的変数の相関比を求めることができないのでこちらを参考に関数を用意しました。
def corr_ratio(x, y):
variation = ((x - x.mean()) ** 2).sum()
inter_class = sum([((x[y == i] - x[y == i].mean()) ** 2).sum() for i in np.unique(y)])
return 1 - (inter_class / variation)
ratios = pd.Series([], index=[])
def get_corr_ratio(col):
set = df_cat.loc[:,[df_cat.columns[col], 'SalePrice']].dropna()
j = set[df_cat.columns[col]]
k = set['SalePrice']
result = corr_ratio(k, j)
return result
def set_corr_ratio(col):
global ratios
ratios[df_cat.columns[col]] = get_corr_ratio(col)
for i in range(43):
set_corr_ratio(i)
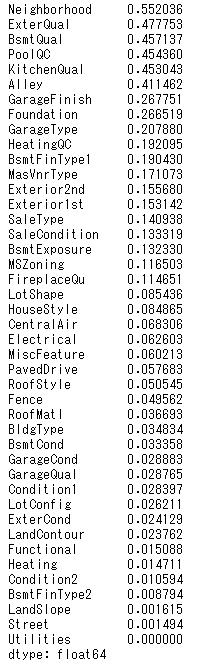
ratios.sort_values(ascending=False)
index_c = ['Neighborhood', 'ExterQual', 'BsmtQual', 'KitchenQual']
fig = plt.figure(figsize=(12,12))
for i in range(4):
ax = fig.add_subplot(2,2,i+1)
sns.boxplot(x=index_c[i], y='SalePrice', data=df_cat)
plt.tight_layout()
plt.show()
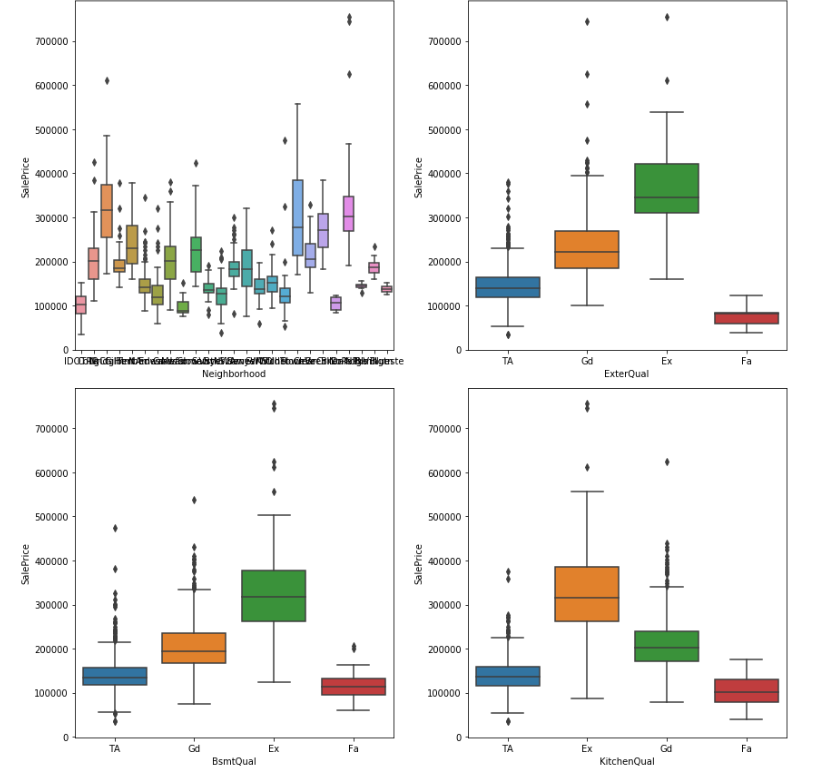
[上位4つの箱ひげ図]
Neighborhoodは細かすぎですし、他は互いに強い相関がみられるので今回はExterQualのみ選択しました。
質的変数の欠損値
省略
欠損値には最頻値をあてる。
pipeline
scikit-learnには便利な機能があり、pipelineを用いて一気に処理することができます。
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
# 量的変数。欠損値に中央値をいれて、標準化
num_pipeline = Pipeline([
('imputer', SimpleImputer(strategy="median")),
('std_scaler', StandardScaler()),
])
# 質的変数。欠損値に最頻値をいれて、ワンホット表現に変換。
cat_pipeline = Pipeline([
('imputer', SimpleImputer(strategy="most_frequent")),
('cat_encoder', OneHotEncoder(sparse=False))
])
# 変数を選択
num_attribs = list(df_num)
cat_attribs = index_c
# pipeline全体を定義
full_pipeline = ColumnTransformer([
("num", num_pipeline, num_attribs),
("cat", cat_pipeline, cat_attribs),
])
df_prepared = full_pipeline.fit_transform(df)
モデルの選択と学習
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(df_prepared, df_labels)
from sklearn.metrics import mean_squared_error
df_predictions = lin_reg.predict(df_prepared)
lin_mse = mean_squared_error(df_labels, df_predictions)
lin_rmse = np.sqrt(lin_mse)
lin_rmse
誤差:38072.084984822926
交差検証
この本の中では決定木を用いる方法も書いてあるが割愛します。
from sklearn.model_selection import cross_val_score
def display_scores(scores):
print("Scores:", scores)
print("Mean:", scores.mean())
print("Standard deviation:", scores.std())
lin_scores = cross_val_score(lin_reg, df_prepared, df_labels,
scoring="neg_mean_squared_error", cv=10)
lin_rmse_scores = np.sqrt(-lin_scores)
display_scores(lin_rmse_scores)
グリッドサーチ
現段階では理解が不十分のためそのまま書き写すにとどまる。
from sklearn.model_selection import GridSearchCV
param_grid = [
{'n_estimators': [3, 10, 30], 'max_features': [2, 4, 6, 8]},
{'bootstrap': [False], 'n_estimators': [3, 10], 'max_features': [2, 3, 4]},
]
orest_reg = RandomForestRegressor(random_state=42)
grid_search = GridSearchCV(forest_reg, param_grid, cv=5,
scoring='neg_mean_squared_error', return_train_score=True)
grid_search.fit(df_prepared, df_labels)
各変数の重要度
feature_importances = grid_search.best_estimator_.feature_importances_
cat_one_hot_attribs = list(full_pipeline.transformers_[1][1].steps[1][1].categories_[0])
attributes = num_attribs + cat_one_hot_attribs
sorted(zip(feature_importances, attributes), reverse=True)
予測
df_test = pd.read_csv("input/test.csv")
df_test["YearBuilt_cat"] = pd.cut(df["YearBuilt"],
bins=[1870, 1920, 1940, 1960, 1980, 2000, np.inf],
labels=[1, 2, 3, 4, 5, 6])
X_test = df_test
X_test_prepared = full_pipeline.transform(X_test)
final_predictions = final_model.predict(X_test_prepared)
submit_data = pd.Series(final_predictions, name='SalePrice', index=df_test['Id'])
submit_data.to_csv('submit.csv', header=True)
kaggleに提出した結果:0.16904(RMSE)
前回適当にもとめた結果が0.30891なので大分改善されました。
参考
[1] scikit-learn(サイキットラーン)とTensorFlowによる実践機械学習, Aurelien Geron, 下田倫大, 長尾高弘, オライリー・ジャパン, 2018
所感
とにかく動かして覚えることを目的にコードを組み立てました。体系的に書かれた本を模倣することで枝の折れた枯れ木をつくることができたと思います。
形式上予測をすることができるようになりましたが、まだまだ基礎的な知識や精度を高める技法も分かっていません。この本を通じてもう少し概要を学び、形から学んでいこうと思います。