ペントミノをExact cover問題として解く（その３）

前回の（その２）ではDLX package を使って簡単なExact cover問題を解く方法を解説しました。

いよいよペントミノ（回転・鏡映あり）を解いていきたいと思います

6. 回転・鏡映をしたピースのデータを作る

その１で定義したpentominoを元にそれを回転・鏡映したデータを作ります。

• 各ピースの回転を４つ、それを鏡映したもの計８個を作る
• 座標の原点を揃えてsetに入れ同じものを除く

この結果63個のピースのデータが得られました

# (Rotate/Reflect (Max 8) version) convert x-y to complex number
def rotate(shape):
    return [(y, -x) for x, y in shape]
def reflect(shape):
    return [(-x, y) for x, y in shape]
def normalize(shape):
    min_x = min(x for x, y in shape)
    min_y = min(y for x, y in shape)
    shape = sorted((x - min_x, y - min_y) for x, y in shape)
    shape = [addxy(xy,shape[0],-1) for xy in shape]
    return shape
def generate_variants(shape):
    variants = set()
    for _ in range(4):
        shape = rotate(shape)
        for refl in [shape, reflect(shape)]:
            norm = tuple(normalize(refl))
            variants.add(norm)
    return list(variants)
pieces = []
for pn, shape in enumerate(pentomino):
  for v, vs in enumerate(generate_variants(shape)):
    pc = [(pn,v), normalize(vs)]   # [(piece number, valiant number), [piece data]]
    print(pc)
    pieces += [pc]
print(len(pieces))
# [(0, 0), [(0, 0), (1, -1), (1, 0), (2, 0), (2, 1)]]
# [(0, 1), [(0, 0), (1, -1), (1, 0), (1, 1), (2, 1)]]
        :                         :
# [(11, 3), [(0, 0), (1, -2), (1, -1), (1, 0), (2, -2)]]
# 63

7. ペントミノをExact Cover問題として考える

以下のように考えることでペントミノをExact Cover問題に変換出来ます

1. 全体集合 Xをすべてのボードのセル（x60）＋ピースID (x12)の72個の集合として、列名とする
2. 各ピースの変形をボードに置いたときの各セル(x5) * ピースID(x1)を行データとする

すなわち列のデータは以下のようになり

	0	1	2	...	59	60	61	...	71
	(0, 0)	(1, 0)	(2, 0)	...	(9,5)	F	I	...	Z

行のデータは例えばIの横向きピースを(0,0)に置いたときは

$[(0,0)(1,0),(2,0),(3,0),(4,0),I]$となる

するとペントミノは全ての行のデータを部分集合と考えると、これを組み合わせて過不足なくすべての列をカバーするものを見つけるExact Cover問題と考えることが出来ます

8. DLXを用いて回転・鏡映ありで10x6の長方形を解く

これで準備がそろったので、コーディングしていきます。

8.1 （ボード＋ペントミノID）の列データを作る

ボードのデータはシンプルですがポイントはset型で定義することです。
このあと（その４）でボードの形を変えて解いていきますが、この２行を書き換えるだけで対応出来ます。

X, Y = 10, 6
boardset = {(x,y) for y in range(Y) for x in range(X)} 

DLXに渡す列データはちょっと工夫が必要です。DLXでは最後に答えの列名のリストを得たときに順番が変わってしまうという問題があり、元に戻すときにソートをする必要があります。ピースIDにFなどの文字を使うとうまく行かないので、ピースID=(ピース番号+100,0)の形にしておきます

columns = [(bn, 0) for bn in boardset]+[((pn+100,0),0) for pn in range(len(pentomino))]
colidx = {cname[0]: i for i, cname in enumerate(columns)}    # column index
print(colidx)
dlx = DLX(columns)
# {(0, 0): 0, (1, 0): 1, ... (9, 5): 59, (100, 0):m ... (111, 0): 71}

8.2 各ピースをボードに置いた行データを入力

各ピースをボードのすべての場所に置いて、置けたら行データとして追加していきます。置けるかの判定はその１で説明したようにsetを使って簡単に行えます

for (pn,v), pc in pieces:
  for bn in boardset:  # move all over the board
    cells = {addxy(bn,p) for p in pc}   # get moved piece
    if cells <= boardset:               # if piece in the board
      dlx.appendRow(sorted([colidx[c] for c in cells]+[len(boardset)+pn]))   # add row

8.3 解答を取り出す

これで入力が終わったのでsolveを呼んで解答を取り出します。今回は期待通りたくさん出てきているので最初の5個だけプリントしました。

#----- Solve! -----
for k, solution in enumerate(dlx.solve()):
  ans = [sorted(dlx.getRowList(i))for i in solution]
  print(k, ans)
  if k > 3: break
# 0 [[(1, 1), (2, 0), (2, 1), (2, 2), (3, 1), (109, 0)], [(0, 0), (0, 1), (0, 2), (0, 3), (1, 0), (102, 0)], [(3, 0), (4, 0), (4, 1), (4, 2), (5, 1), (100, 0)], [(5, 0), (6, 0), (6, 1), (6, 2), (7, 0), (105, 0)], [(1, 2), (1, 3), (2, 3), (3, 2), (3, 3), (106, 0)], [(0, 4), (0, 5), (1, 4), (1, 5), (2, 4), (104, 0)], [(2, 5), (3, 5), (4, 5), (5, 5), (6, 5), (101, 0)], [(5, 2), (5, 3), (6, 3), (7, 3), (7, 4), (111, 0)], [(3, 4), (4, 3), (4, 4), (5, 4), (6, 4), (110, 0)], [(7, 5), (8, 5), (9, 3), (9, 4), (9, 5), (107, 0)], [(7, 1), (7, 2), (8, 0), (8, 1), (9, 0), (108, 0)], [(8, 2), (8, 3), (8, 4), (9, 1), (9, 2), (103, 0)]]
# 1 [[(1, 1), (2, 0), (2, 1), (2, 2), (3, 1), (109, 0)], [(0, 0), (0, 1), (0, 2), (0, 3), (1, 0), (102, 0)], [(3, 0), (4, 0), (5, 0), (6, 0), (7, 0), (101, 0)], [(0, 4), (1, 2), (1, 3), (1, 4), (2, 3), (100, 0)], [(0, 5), (1, 5), (2, 4), (2, 5), (3, 4), (103, 0)], [(3, 5), (4, 3), (4, 4), (4, 5), (5, 5), (105, 0)], [(3, 2), (3, 3), (4, 2), (5, 2), (5, 3), (106, 0)], [(4, 1), (5, 1), (6, 1), (6, 2), (6, 3), (107, 0)], [(5, 4), (6, 4), (6, 5), (7, 4), (7, 5), (104, 0)], [(7, 3), (8, 3), (8, 4), (8, 5), (9, 5), (111, 0)], [(7, 1), (7, 2), (8, 0), (8, 1), (9, 0), (108, 0)], [(8, 2), (9, 1), (9, 2), (9, 3), (9, 4), (110, 0)]]
# 2 [[(1, 1), (2, 0), (2, 1), (2, 2), (3, 1), (109, 0)], [(0, 0), (0, 1), (0, 2), (0, 3), (1, 0), (102, 0)], [(3, 0), (4, 0), (5, 0), (6, 0), (7, 0), (101, 0)], [(0, 4), (1, 2), (1, 3), (1, 4), (2, 3), (100, 0)], [(0, 5), (1, 5), (2, 4), (2, 5), (3, 4), (103, 0)], [(3, 5), (4, 3), (4, 4), (4, 5), (5, 5), (105, 0)], [(3, 2), (3, 3), (4, 1), (4, 2), (5, 1), (108, 0)], [(7, 2), (8, 2), (9, 0), (9, 1), (9, 2), (107, 0)], [(6, 1), (6, 2), (7, 1), (8, 0), (8, 1), (111, 0)], [(5, 2), (5, 3), (5, 4), (6, 3), (6, 4), (104, 0)], [(6, 5), (7, 5), (8, 4), (8, 5), (9, 5), (110, 0)], [(7, 3), (7, 4), (8, 3), (9, 3), (9, 4), (106, 0)]]
# 3 [[(1, 1), (2, 0), (2, 1), (2, 2), (3, 1), (109, 0)], [(0, 0), (0, 1), (0, 2), (0, 3), (1, 0), (102, 0)], [(3, 0), (4, 0), (5, 0), (6, 0), (7, 0), (101, 0)], [(0, 4), (0, 5), (1, 2), (1, 3), (1, 4), (103, 0)], [(1, 5), (2, 3), (2, 4), (2, 5), (3, 4), (100, 0)], [(3, 5), (4, 3), (4, 4), (4, 5), (5, 5), (105, 0)], [(3, 2), (3, 3), (4, 2), (5, 2), (5, 3), (106, 0)], [(4, 1), (5, 1), (6, 1), (6, 2), (6, 3), (107, 0)], [(5, 4), (6, 4), (6, 5), (7, 4), (7, 5), (104, 0)], [(7, 3), (8, 3), (8, 4), (8, 5), (9, 5), (111, 0)], [(7, 1), (7, 2), (8, 0), (8, 1), (9, 0), (108, 0)], [(8, 2), (9, 1), (9, 2), (9, 3), (9, 4), (110, 0)]]
# 4 [[(1, 1), (2, 0), (2, 1), (2, 2), (3, 1), (109, 0)], [(0, 0), (0, 1), (0, 2), (0, 3), (1, 0), (102, 0)], [(3, 0), (4, 0), (5, 0), (6, 0), (7, 0), (101, 0)], [(0, 4), (0, 5), (1, 2), (1, 3), (1, 4), (103, 0)], [(1, 5), (2, 3), (2, 4), (2, 5), (3, 4), (100, 0)], [(3, 5), (4, 3), (4, 4), (4, 5), (5, 5), (105, 0)], [(3, 2), (3, 3), (4, 1), (4, 2), (5, 1), (108, 0)], [(7, 2), (8, 2), (9, 0), (9, 1), (9, 2), (107, 0)], [(6, 1), (6, 2), (7, 1), (8, 0), (8, 1), (111, 0)], [(5, 2), (5, 3), (5, 4), (6, 3), (6, 4), (104, 0)], [(6, 5), (7, 5), (8, 4), (8, 5), (9, 5), (110, 0)], [(7, 3), (7, 4), (8, 3), (9, 3), (9, 4), (106, 0)]]

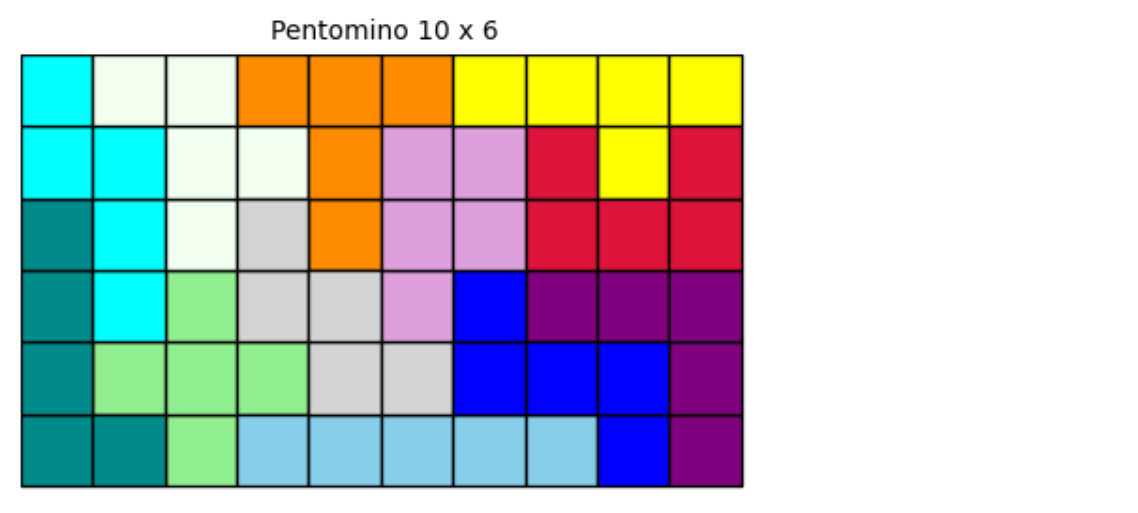
8.3 解答を表示

この最後の#4を表示させます。

8.4 すべての答えは？

このコードをbreakしないで最後まで走らせると9356個の解答が出力されます。この解答から上下・左右・180度回転で同じになるものを除くと期待通り2339個の解答が得られました。（そのコードは今回は省略します）

さすがに全部は表示出来ないので最初の50個と最後の49個を以下に表示します。

次回（その４）ではボードの形を変えた問題を解きます。

解答： 0-99

解答： 2290-2398

（開発環境：Google Colab）