バーンサイドの補題(Wikipedia)でも紹介されているように例題としてよく取り上げられる立方体の塗り分け問題をSagemathのCycle Indexを用いて解いてみます。
【例題 1】立方体の面を3色で塗り分ける数を求める(回転して同じになるものは1つと数える)
1.(正六面体)の面の置換群を求める
まず立方体(正六面体)の面の置換群を求める必要があります。上記のWikiでも24通りの置換を手計算で求めていますが、Sagemathを使って求める方法がSage Tutorials: Group Theory and Sageで説明されています。
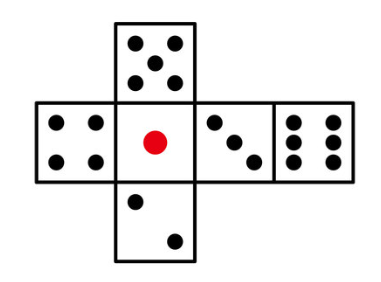
分かりやすいように正六面体に下のサイコロのように番号が振られているとします。基本的なサイコロの面の移動方法は以下の3つで、それぞれの場合に各面が置換を巡回置換表現で表します。この3つの置換が(正六面体)の面の置換群の生成元と考えられます。
| 移動方法 | 巡回置換表現 |
|---|---|
| 縦に90度ころがす | $(1265)$ |
| 横に90度ころがす] | $(1364)$ |
| 水平に90度回す | $(2354)$ |
2. Sagemathで置換群を求める
この生成元を使ってSagemathで置換群を求めます。24個の置換が求まっているのが分かります。
cubeface = PermutationGroup(["(1,3,6,4)", "(1,2,6,5)", "(2,3,5,4)"])
cubeface.list()
# [(), (2,5)(3,4), (1,4,5)(2,6,3), (1,4,2)(3,5,6), (1,5,4)(2,3,6), (1,5,3)(2,4,6), (1,6)(3,4), (1,6)(2,5), (1,3,5)(2,6,4), (1,3,2)(4,5,6), (1,2,3)(4,6,5), (1,2,4)(3,6,5), (1,3,6,4), (1,4)(2,5)(3,6), (1,2,6,5), (1,5,6,2), (1,6)(2,3)(4,5), (2,4,5,3), (1,4,6,3), (1,3)(2,5)(4,6), (1,5)(2,6)(3,4), (1,2)(3,4)(5,6), (2,3,5,4), (1,6)(2,4)(3,5)]
この正六面体群が対照群$S4$と同型であることも分かります。
cubeface.is_isomorphic(SymmetricGroup(4))
# True
3. Cycle Indexを求めて例題を解く
正六面体群が求まったらCycle Indexを求めて3を代入すれば答えの$57$が求まります。
この詳細はSagemathのCycle Indexを用いてピザの色分け問題を解く(その1)を参考にしてください。
P = cubeface.cycle_index();P
sum([i[1]*prod([3 for j in i[0]]) for i in P])
#1/24*p[1, 1, 1, 1, 1, 1] + 1/8*p[2, 2, 1, 1] + 1/4*p[2, 2, 2] + 1/3*p[3, 3] + 1/4*p[4, 1, 1]
#57
(開発環境:CoCalc, Sage Worksheet)