前回バーンサイドの補題を用いてピザの色分け問題を解くという投稿をしました。今回はこれをSagemathのCycle Index(巡回指数)の機能を用いてより一般的な問題を解くことを目標とします。
まずは巡回指数というものを少しでも理解するために、色を使う回数に制限がない場合から見て行きます。
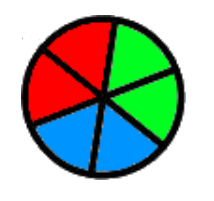
【例題 1】ピザの色分け問題 (3色・制限なし)
以下のように6個に切ったピザを3色で塗る方法は何通りあるでしょう。各色は何度使っても(使わなくても)良い。(回転したものは同じとみなす)
以下の手順で考えて行きます。
- 群の置換を巡回置換表現で表す
- 巡回指数を求める
- 式に色の数を代入
1. 群の置換を巡回置換表現で表す
巡回群C6なので6通りの回転を以下のように巡回置換表現で表し巡回指数の各項が出てきます。
| 回転置換 | 巡回置換表現 | 巡回指数の項 |
|---|---|---|
| [123456] | (1)(2)(3)(4)(5)(6) | $a_1^6$ |
| [234561] | (123456) | $a_6$ |
| [345612] | (135)(246) | $a_3^2$ |
| [456123] | (14)(25)(36) | $a_2^3$ |
| [561234] | (153)(264) | $a_3^2$ |
| [612345] | (165432) | $a_6$ |
2. 巡回指数を求める
巡回指数の各項を足してC6の位数6で割ると以下のように巡回指数$Z(C_6)$が求まります。詳しくはCycle index (Wikipedia)(英語)を参考にしてください。
Z(C_6) = \frac{1}{6}(a_1^6+a_2^3+2a_3^2+2a_6)
3. 式に色の数を代入
この巡回指数からバーンサイドの補題のポイント 「回転して同じ形になるもの数を数えて回転の種類の数で割ったもの」 を利用して数え上げをして行きます。
例えば$a_3=(135)$に注目するとこれは$120^\circ$回転したときに$(135)$の色が同じになるということなので$a_3=3$(赤か緑か青)と置けます。同様にすべての$a_i=3$となるので、以下のように解答が得られます。
Z(C_6) = \frac{1}{6}(3^6+3^3+2 \times 3^2+2 \times 3) \\
= (729+27+18+6) / 6 = 130
Sagemathで解く
この手順をSagemathを使って計算していきます。まず巡回群C6を定義して巡回置換表現をリストしてみます。単位元の
$(1)(2)(3)(4)(5)(6)$は$()$で表されています。
S = CyclicPermutationGroup(6)
S.list()
# [(), (1,2,3,4,5,6), (1,3,5)(2,4,6), (1,4)(2,5)(3,6), (1,5,3)(2,6,4), (1,6,5,4,3,2)]
つぎに巡回指数(Cycle Index)を求めます。ちょっと表現が分かりずらいですが。$p[2,2,2]=a_2^3$という感じでざっくり理解してもらえばいいと思います。
P = S.cycle_index();P
# 1/6*p[1, 1, 1, 1, 1, 1] + 1/6*p[2, 2, 2] + 1/3*p[3, 3] + 1/3*p[6]
後はこの$p$の中の数に3を代入して計算して答えの130が得られました。
sum([i[1]*prod([3 for j in i[0]]) for i in P])
# 130
これだけだとそれほどSagemathのすごさは感じられませんが、後編のその2で十分にすごさが堪能できますので楽しみにしてください。
(開発環境:CoCalc, Sage Worksheet)