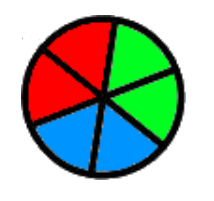
【例題】ピザの色分け問題
以下のように6個に切ったピザを3色で2個づつ塗る方法は何通りあるでしょう(回転したものは同じとみなす)
単純に円順列で考えると⁈
単純に円順列=(線順列/個数)で考えると$6!/2!2!2! \div 6 = 15$となりますが、残念ながら不正解です。この式はすべてのパターンが周期6を仮定していますが、なかに[1,2,3,1,2,3]のように周期が3の物があるからです。
バーンサイドの補題
そこでバーンサイドの補題(Wikipedia)の出番となります。
|X/G| = \frac{1}{|G|}\sum_{g \in G}|X^g|
この式を見てもなんのこっちゃという感じですが。円順列で考えると 「回転して同じ形になるもの数を数えて回転の種類の数で割ったもの」 ということになります。
従って例題の場合だと、
- $0^{\circ}$回転で同じになるものは線順列そのものなので$6!/2!2!2! = 90$
- $180^{\circ}$回転で同じになるもの[1,2,3,1,2,3]のパターンで[1,2,3]の順列が$3! = 6$
- 合計が96なので回転の種類の数6で割って、答えは16となります。
バーンサイドの補題のプログラム(その1)
この考えを一般化して$m$色で$n$個ずつ塗った時の円順列を計算するプログラムと書いて行きます。まずはバーンサイドの補題を忠実に実装します。
- 線順列のパターンをすべて生成する(distinct_permutations)
- 各々のパターンを回転して行き1周する前に重なるものを数える(np.roll)
- 1.と2.を足して$m \times n$で割る
2.の回転で重なるものをprintしているので6種類のパターンを出ていることが分かります。
from more_itertools import distinct_permutations
import numpy as np
def f1(m,n):
s = [i+1 for i in range(m) for k in range(n)]
print(f"s={s}")
c1, c2 = 0, 0
for p in distinct_permutations(s):
p = np.array(p)
for k in range(1,len(s)):
p2 = np.roll(p,k)
if np.all(p==p2):
c2 += 1
print(k,p)
c1 += 1
return (c1+c2)//(len(s))
m, n = 3,2
print(f"f1({m},{n}) = {f1(m, n)}")
#s=[1, 1, 2, 2, 3, 3]
#3 [1 2 3 1 2 3]
#3 [1 3 2 1 3 2]
#3 [2 1 3 2 1 3]
#3 [2 3 1 2 3 1]
#3 [3 1 2 3 1 2]
#3 [3 2 1 3 2 1]
#f1(3,2) = 16
バーンサイドの補題のプログラム(その2)
その1のプログラムは忠実に実装しているのでパターンがどんなものであっても正解がでるのですが、あまり効率的とは言えません。
$m$色で$n$個ずつ塗った時の円順列のように規則性があるパターンの場合には、以下のように約数を使って考えると計算のみで答えを出すことが出来ます。
- $G = m \times n$の約数でmの倍数のもの $d_i$とする(例題では2)
- $d_i$はmの倍数なので元のパターンを$d_i$個に分割できる。(例題では[1,2,3])
- この分割したパターンの順列の数を$mg[d_i]$とする(例題では6)
- $d_i$の大きい方からその倍数で3.でまだ値を求めてないものがあれば$mg[d_i]$と同じ値にする(例題ではなし)
- これらの合計をとってGで割る
プログラムにすると以下になります。dpermは同じものを含む順列の数を返す関数です。
ここではf2(2,6)を求めていますが、3.のケースが8と10で現れています。
- mg[8] = mg[4]
- mg[10] = mg[2] (他の2の倍数の4,6,8は既に値が求まっている)
import sympy
from math import factorial as fct
def dperm(a): # number of distinct permutation
ret = fct(sum(a))
for r in a:
ret //= fct(r)
return ret
def f2(m,n):
G = m*n
di = list(reversed([d for d in sympy.divisors(G) if d % m == 0 and d < G]))
mg = [0]*(G+1)
mg[G] = dperm([n]*m)
for d in di:
mg[d] = dperm([d//m]*m)
for i in range(2, G//d):
if mg[d*i] == 0: mg[d*i] = mg[d]
print(f"m,n = {m},{n}, G = {G}, di={di}, mg = {mg}")
return sum(mg)//
m, n = 2,6
print(f"f2({m},{n}) = {f2(m, n)}")
#m,n = 2,6, G = 12, di=[6, 4, 2], mg = [0, 0, 2, 0, 6, 0, 20, 0, 6, 0, #2, 0, 924]
f2(2,6) = 80
(開発環境:Google Colab)
この考え方はProject Euler: Problem 281 Pizza Toppingsを解くのに役に立ちます。