Transformerとは
Transformerは、NLPで主に使用される深層学習アーキテクチャの一つです。Transformerが出現した後、様々なタスクに活用されていたRNNとLSTMはTransformerに置き換えられました。そしてBERT, GPT, T5などのNLPモデルにTransformerアーキテクチャが適用されました。
この記事ではTransformerの基本的な意味から構造まで説明します。この記事、Encoder編で扱うTransformer内容は次の2件です。
- Transformerの全体的な構造紹介
- TransformerのEncoder理解
そしてDecoder編では続いて次の3つの主題を取り上げます。
- TransformerのDecoder理解
- EncoderとDecoderの結合
- Transformerの学習
この記事ではコードを用いた説明は行いません。数字だけを利用した例でTransformerの構造を説明します。
Decoder編は以下を参照してください。
Transformer紹介
RNNとLSTMネットワークは、次の単語予測、機械翻訳、テキスト生成などの順次タスクで広く使用されます。しかし、このネットワークには長期依存性の問題があります。このRNNの限界点を克服するために、「Attention is all you need」でTransformerというアーキテクチャを提案しました。Transformerは現在、様々なNLP課題で最新技術として使用されています。Transformerの登場により自然言語処理分野は画期的に発展し、BERT, GPT-3, T5などの革命的なアーキテクチャが発展する基盤が作られました。
TransformerはRNNで使用した循環方式を使わず、純粋にAttentionだけを利用したモデルです。Transformerはself-attentionという特殊な形態のattentionを使用します。次節では、self-attentionの作動原理を詳しく数学的計算を通じて説明します。
まず、機械翻訳課題を通じてTransformerがどのような原理で作動するのかから説明します。TransformerはEncoder-Decoderで構成された深層学習モデルです。Encoderに原文を入力すると、Encoderは原文の表現を学習した後、その結果をDecoderに送信します。そして、DecoderはEncoderで学習した表現結果を入力してもらい、ユーザーが望む文章を生成します。
例えば、英語をフランス語に翻訳する課題があるとします。下の図は英語の文章を入力されたEncoderを示しています。Encoderは英語の文章を表現する方法を学習して、その結果をDecoderに送ります。そしてEncoderで学習した表現を入力されたDecoderは、最終的にフランス語に翻訳した文章を生成します。
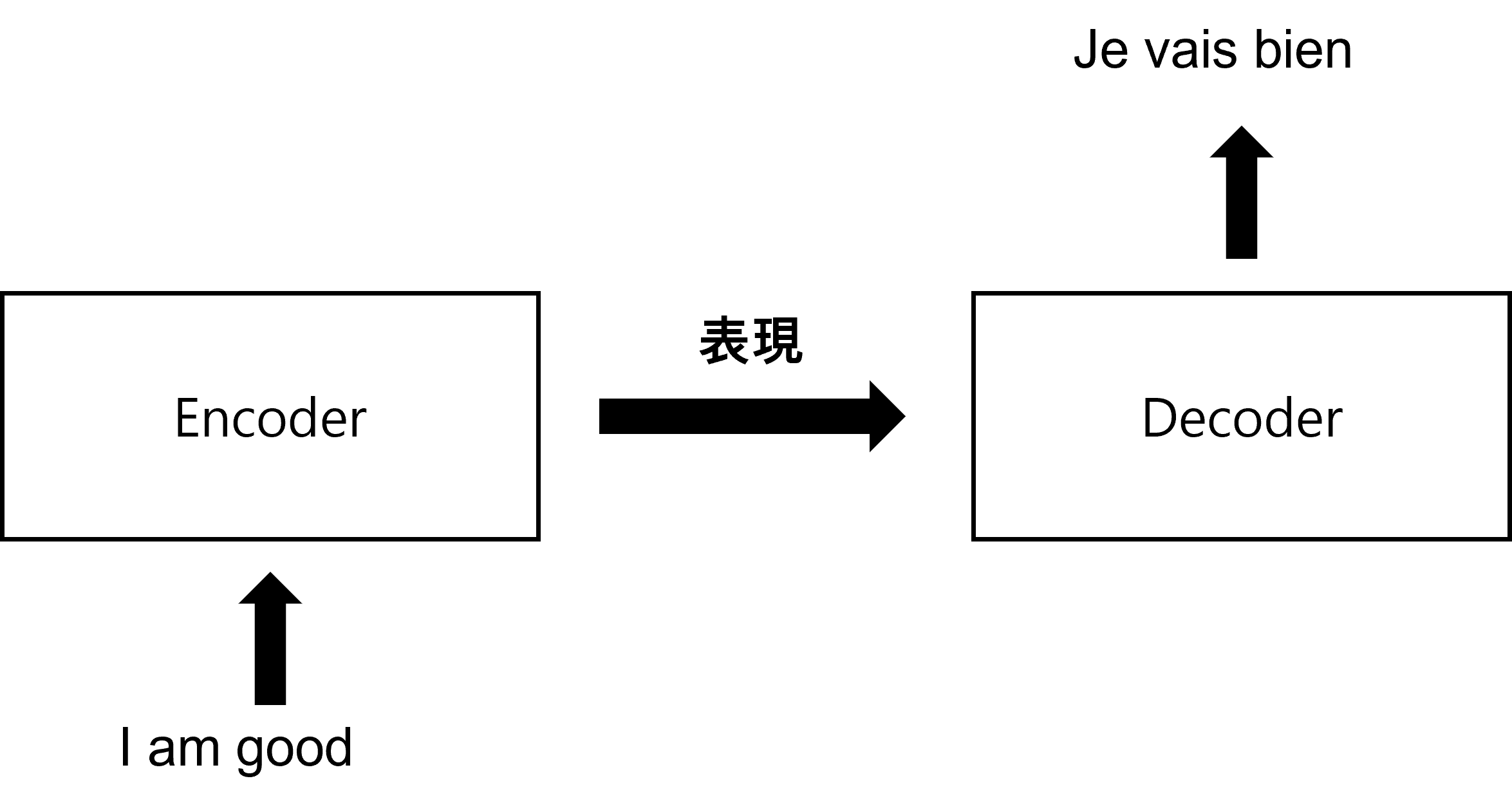
このTransformerはどのように動作するのでしょうか?TransformerのEncoder-Decoderは英語文章をどのようにフランス語文章に変形するのでしょうか?そしてEncoderとDecoderの原理は何でしょうか?次節からはEncoderから詳しく説明します。
TransformerのEncoder理解
TransformerはN個のEncoderが積まれた形です。TransformerはN個のEncoderが積まれた形です。Encoderの結果値は、次のEncoderの入力値に入ります。下の図はEncoderがN個に積まれている形を示しています。一番最後にあるEncoderの結果値が入力値の最終表現結果になります。
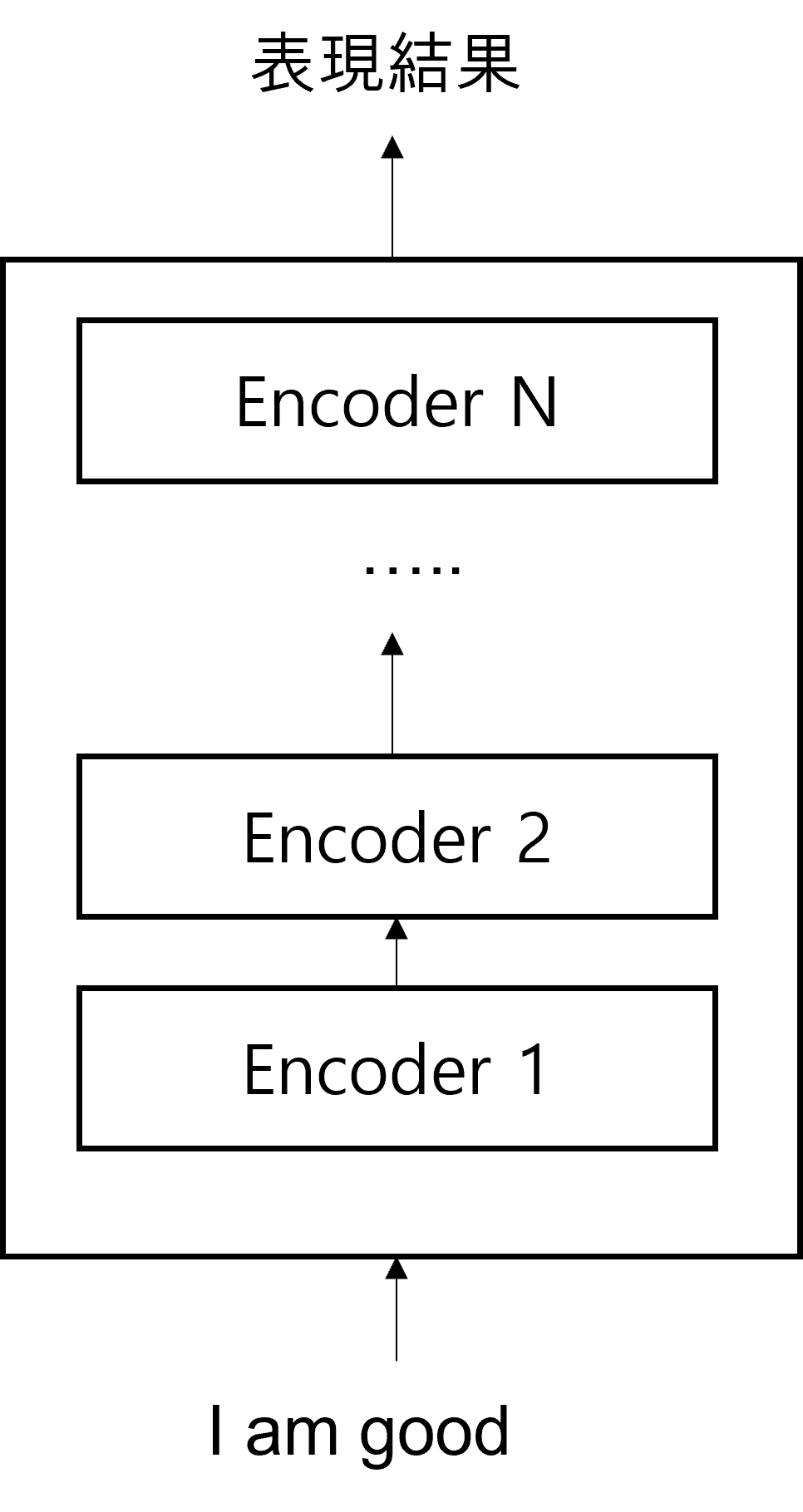
Transformerを紹介した論文である「Attention Is All You Need」で$N=6$となっています。これはEncoderを6つ累積して積み上げた形を表現したものです。
Encoderの原理を理解するには、Encoderの構成要素を理解する必要があります。Encoderの詳細構成要素を表現すると、次のようになります。

Encoderの構成要素を見ると、すべてのEncoder blockの形が同じです。また、Encoder blockは2つの要素で構成されています。
- Multi-head Attention
- Feed Forward Network
この2つの要素がどのように機能するかを理解するために、まずMulti-head Attentionの基本原理であるSelf-Attentionの作動原理について説明します。
Self-Attentionの作動原理
例を用いてSelf-Attentionの作動原理を説明します。まず、次のような文章があると仮定します。
- A cat drank the water because it was thirsty.
この文章で「it」は「cat」や「water」を意味します。人はこの文章を読んで、「it」が「cat」であることを簡単に知ることができます。しかし、機械はこれをどのように判断できるのでしょうか?この時、Self-Attentionが必要です。
この文章が入力されたとき、モデルは最初に単語「A」の表現を、その次に単語「cat」の表現を計算してから「drank」という単語の表現を順番に計算します。それぞれの単語を計算する間、各単語の表現は文章の中にある他のすべての単語の表現と連結して単語が文章内で持つ意味を理解します。例えば、「it」という単語の表現を計算している間、モデルでは「it」という単語の意味を理解するために文章の中にあるすべての単語と「it」という単語を連結する作業を行います。
下の図は、「it」という単語の表現を計算するために、「it」を文章のすべての単語と関連付ける作業を示しています。このような接続作業で、モデルは「it」が「water」ではなく「cat」と関連があることを学びます。「cat」を連結する線が他の単語より厚く表示され、これは「it」という単語が「water」ではなく「cat」と関連があることを示しています。

簡単な例を通じて、Self-Attentionがなぜ必要なのかを知ったので、これからSelf-Attentionの内部作動原理を詳しく説明します。
入力文が「I am good」であると仮定します。 この文章を基準に、各単語のembeddingを抽出します。 ここでembeddingとは、それぞれの単語を表現するベクトル値を意味し、embedding値はモデルの学習過程で一緒に学習されます。
$x_{1}$を「I」、$x_{2}$を「am」、$x_{3}$は「good」に対するembedding値と仮定します。それぞれのembedding値を表現すると、次のようになります。
- 単語「I」に対するembedding値:$x_{1}$ = [2.34, 1.54, ..., 7.64]
- 単語「am」に対するembedding値:$x_{2}$ = [8.53, 1.42, ..., 6.43]
- 単語「good」に対するembedding値:$x_{3}$ = [9.23, 8.95, ..., 2.58]
それでは入力文「I am good」を下のようにEmbedding行列(入力行列)で表現することができます。

入力行列の初期値は任意に設定しました。
入力行列で1行目は「I」のEmbedding、2行目は「am」のEmbedding、3行目は「good」のEmbeddingを意味します。この時、Embedding行列の次元は[文章の長さ X Embedding次元]の形になります。上記の文章の長さは3で、Embedding次元は512だと仮定すると、入力行列の次元は[3 X 512]になります。
次は入力行列からQuery, Key, Value行列を生成します。この行列を作るためには、${W_{}}^{Q}$, ${W_{}}^{K}$, ${W_{}}^{V}$という3つのweight matrixを入力行列に掛けてQ, K, V行列を生成します。このとき、weight matrix ${W_{}}^{Q}$, ${W_{}}^{K}$, ${W_{}}^{V}$は最初は任意の値を持ち、学習過程で最適値を得ます。学習を通じて最適なweight matrix値が生成されると、より正確なQuery値、Key値、Value値が得られます。
下の図に示すように、入力行列値からweight matrix${W_{}}^{Q}$, ${W_{}}^{K}$, ${W_{}}^{V}$をかけるとQuery, Key, Value値が得られます。

上の図から次の3つの内容を確認することができます。
- Query, Key, Valueの1行目である$q_{1}$, $k_{1}$, $v_{1}$は単語「I」に対するQuery, Key, Valueを意味する。
- Query, Key, Valueの2行目である$q_{2}$, $k_{2}$, $v_{2}$は単語「am」に対するQuery, Key, Valueを意味する。
- Query, Key, Valueの3行目である$q_{3}$, $k_{3}$, $v_{3}$は単語「good」に対するQuery, Key, Valueを意味する。
ここでQuery, Key, Valueベクトルの次元が64だと仮定すると、Query, Key, Value行列の次元は[文章の長さ X 64]になります。例文である「I am good」は3つの単語を持っているので、次元は[3 X 64]になります。
次は、なぜこのような方法を利用して計算するのか、Query, Key, Value行列はどのように使われるのかなどについて説明します。
Self-Attentionの作動原理の解説
単語の表現を計算するため、Self-Attentionは各単語を基準に与えられた文章にあるすべての単語と連結する過程を遂行すると説明しました。この方法は、特定の単語と文章内にあるすべての単語がどのように関連しているのかを理解すると、より良い表現を学習させるために役立つので利用する方法です。そしてSelf-AttentionのQuery, Key, Valueは特定の単語と文章内にあるすべての単語を連結するために使用されます。これを4つの段階に分けて説明します。
1つ目:内積計算による類似度抽出
Self-Attentionの第一段階は、Query行列(Query)とKey行列(${K_{}}^{T}$)の転置行列の内積演算を行います。

Query行列(Query)とKeyの転置行列${K_{}}^{T}$の内積演算結果は次のとおりです。

ここで使用された値は任意に設定された値です。
この時、QueryとKey行列の間の内積を計算する理由は何でしょうか?演算結果は正確に何を意味しますか?$Q·{K_{}}^{T}$演算の結果について説明します。
上記の$Q·{K_{}}^{T}$演算で1番目の行を確認します。1番目の行はQueryベクトル$q_{1}$(I)とKeyベクトル$k_{1}$(I), $k_{2}$(am), $k_{3}$(good)の内積を計算することがわかります。2つのベクトル間の内積を計算すると、2つのベクトルがどれほど類似しているかがわかります。
つまりQueryベクトル($q_{1}$)とKeyベクトル($k_{1}$, $k_{2}$, $k_{3}$)の間の内積を計算するのはQueryベクトル$q_{1}$(I)とKeyベクトル$k_{1}$(I), $k_{2}$(am), $k_{3}$(good)との間の類似度を計算したものです。$Q·{K_{}}^{T}$行列の一番目の行を見ると、単語「I」は単語「am」と「good」より自分(I)との関連性が高いことが分かります。$q_{1}·k_{1}$の内積値が$q_{1}·k_{2}$, $q_{1}·k_{3}$より高いからです。

それでは$Q·{K_{}}^{T}$の2番目の行を確認します。2番目の行はQueryベクトル$q_{1}$(am)とKeyベクトル$k_{1}$(I), $k_{2}$(am), $k_{3}$(good)の類似度を計算したものです。
$Q·{K_{}}^{T}$行列の2番目の行を見ると、単語「am」は単語「I」,「good」より自分(am)と関連性が高いことが分かります。$q_{2}·k_{2}$の内積値が$q_{2}·k_{1}$, $q_{2}·k_{3}$より高いからです。

$Q·{K_{}}^{T}$の3番目の行である「good」もまた内的値計算を通じて単語「I」,「am」より自分(good)と関連性が高いことが分かります。したがって、Query行列とKey行列の間の内積を計算すると類似度が得られます。これは、文章の各単語が他のすべての単語とどれほど似ているかを把握するのに役立ちます。
2つ目:Gradient値の安定化
次のステップは、$Q·{K_{}}^{T}$行列をKeyベクトル次元の平方根で割ったものです。この方法を適用すると、安定したgradient値が得られます。
$d_{k}$をKeyベクトルの次元とします。それでは$Q·{K_{}}^{T}$を$\sqrt{d_{k}}$で割ります。今の例ではKeyベクトルの次元は64ですから、64の平方根である8で$Q·{K_{}}^{T}$を分けます。

3つ目:類似度行列の正規化
今まで計算した類似度の値は非正規化された形態(unnormalized form)でした。したがって、Softmax関数を使用して正規化作業を進めます。Softmax関数を適用すると、全体の値の和は1になり、それぞれ0と1の間の値を持ちます。$\frac{Q·{K_{}}^{T}}{\sqrt{d_{k}}}$の結果にSoftmax関数を適用すると、次のような結果が得られます。

この行列をscore行列といいます。この点数を基に、文章内の各単語が文章内の全体単語とどれだけ関連しているかが分かります。例えば、score行列の一番目の行を見ると、単語「I」は自分自身と59%、単語「am」とは31%、「good」とは9%関連していることが分かります。
4つ目:Attention行列計算
Attention行列は、文章のすべての単語のベクトル値を持ちます。前で計算したscore行列の$softmax(\frac{Q·{K_{}}^{T}}{\sqrt{d_{k}}})$にValue行列を掛けると、Attention(Z)行列が得られます。

上記の計算から得られた結果は下のとおりです。

Attention行列は、各点数を基準にweightが付与されたベクトルの和で計算します。計算結果を一行ずつ見てみましょう。まず、一番目の行列$z_{1}$を見ると、単語「I」のSelf-Attentionは次のように計算されます。
上の図ように単語「I」のSelf-Attentionは、各Valueベクトル値の加重値和で計算されます。つまり$z_ {1}$の値は、valueベクトル$v_{1}$(I)の59%値とvalueベクトル$v_{2}$(am)の31%値とvalueベクトル$v_{3}$(good)の9%値の和で求められます。
この計算方法は、単語が文章内にある他の単語とどれだけ関連性があるかを知るメリットがあります。$z_{1}$と同様に、単語「am」のSelf-Attentionである$z_{2}$と単語「good」のSelf-Attentionである$z_{3}$も求めることができます。
つまり、Attention行列は文章内にある単語のSelfベクトル値で構成されていることが分かり、次の式で要約できます。
- $softmax(\frac{Q·{K_{}}^{T}}{\sqrt{d_{k}}})V$
今まで見てきたSelf-Attentionの段階を要約すると、次のようになります。
- Query行列とKey行列間の内積を計算し($Q·{K_{}}^{T}$)類似度値を算出する。
- $Q·{K_{}}^{T}$をKey行列次元の平方根に分ける。
- Score行列にsoftmax関数を適用して正規化する。
- Score行列にvalue行列を掛けてAttention行列Zを求める。
絵で表現すると次のようになります。
Self-AttentionはQueryとKeyベクトルの内積を計算した後、$\sqrt{d_{k}}$に割るため、scaled-dot product attentionとも呼ばれます。
Multi-head Attentionの理解
Attentionを使用する場合、headを1つだけ使用した形態ではなく、headを複数使用したAttention構造も使えます。単一のAttentionではなく、マルチAttention行列のメリットは次の通りです。

「This is apple」という文章で例を挙げましょう。単語「This」のSelfベクトル値は、加重値を適用した各単語のベクトル値の和であることがわかります。上記の内容をより詳しく見ると、単語「This」のベクトル値は単語「This」が最も優勢に作用することが分かります。すなわち、単語「This」のベクトル値は単語「This」のベクトル値に0.4を掛けた値と、単語「apple」のベクトル値に0.6をかけた結果を合わせたものである。これは単語「This」のベクトル値が40%反映され、単語「apple」のベクトル値が40%反映されたものと解釈できます。したがって、「This」のベクトル値は単語「apple」の影響が最も大きいと言えます。
しかし、文章内で単語の意味が曖昧な場合もあります。 次の文章で「it」のSelf-Attentionを計算して、次のような結果を得たと仮定します。
- A cat drank the water because it was thirsty.

一般的な常識では、単語「it」のベクトル値は「cat」に対するベクトル値が高くなければなりません。しかし、例のように意味が合わない単語のベクトル値が高い場合は、文章の意味が間違って解釈されることがあります。そこで、Attention結果の正確度を高めるために、single-head attentionではなくmulti-head attentionを使用した後、その結果値を加える形で進めます。この方法を使う理由は、single-head attentionよりmulti-head attentionの方が正確に文章の意味を理解できるという仮定があるからです。
Multi-head attentionは簡単に計算できます。2つのAttention行列$z_{1}$, $z_{2}$を計算するとします。まず、$z_{1}$値を求めます。説明したAttention行列の計算方法を参考にすると、Query, Key, Value行列を生成し、次に3つのweight行列$w_{1}^{Q}$, $w_{1}^{K}$, $w_{1}^{V}$を生成します。最後に入力行列にweight行列を掛けて$Q_{1}$, $K_{1}$, $K_{1}$行列を求めます。
このAttention行列$z_{1}$は次のように計算されます。
- $z_{1} = softmax(\frac{Q_{1}·{K_{1}}^{T}}{\sqrt{d_{k}}})K_{1}$
2番目のAttention行列$z_{2}$も、1番目のAttention行列$z_{1}$と同じ方式で計算されます。
- $z_{2} = softmax(\frac{Q_{2}·{K_{2}}^{T}}{\sqrt{d_{k}}})K_{2}$
このような方法で8つのAttention行列($z_{1}$~$z_ {8}$)を求めると、それぞれの行列を計算した後、その結果(Attention head)を連結(concatenate)した後、新しいweight行列${W_{}}^{0}$をかけると、最終的に私たちが望む行列を求めることができます。
- Multi-head Attention = concatenate($z_{1}$, $z_{2}$, ..., $z_{8}$)${W_{}}^{0}$
Attention headのi個を連結するとAttention head X iサイズになります。Attention headの最終結果はAttention headの元のサイズなので、サイズを小さくするためにweight行列(${W_{}}^{0}$)を掛けます。
Positional Encodingを利用した単語位置情報学習
「I am good」という入力文があると仮定します。RNNでは、単語単位でネットワークに文章を入力します。順番に単語が入力されるため、順序が重要な自然言語処理に強いという長所がありますが、文章が長くなるほど前の情報が後に十分に伝わらない現象があります。これを長期依存性問題(the problem of Long-Term Dependencies)といいます。
この問題を解決するために、TransformerネットワークではRNNのような循環構造を使用しません。順番に単語を入力する代わりに、文章内のすべての単語を並列形式で入力します。並列に単語を入力することは、学習時間を短縮し、RNNの長期依存性問題を解決するのに役立ちます。
しかし、Transformerで単語を並列に入力すると、単語の順序情報が維持されない問題が発生します。文章の意味を理解するためには、単語の位置情報が非常に重要です。Transformerはこの問題を位置エンコーディング(Positional Encoding)を利用して解決しました。
「I am good」という文章に戻って、文章中の各単語に対してembedding値を求めます。この時、embedding次元を$d_{model}$と言います。 ここでembedding次元の値を4とすると、文章に対する入力行の次元は[文章の長さ X embedding次元] = [3 X 4]になります。
「I am good」という文章を入力行列で表現すると、次のようになります。

入力行列をTransformerに直接入力すると、単語の順序情報が理解できません。つまり、単語の順序を表現する情報を追加で提供しなければなりませんが、そのために位置エンコーディングという新しい方法を活用します。
位置エンコーディング行列Pの次元は入力行列Xの次元と同じです。そのため、入力行列Xに位置エンコーディングPを加えた後、ネットワークに入力することができ、これからは入力行列は単語のembeddingだけでなく文章の単語位置情報も含みます。

位置エンコーディングは、sin波関数を使用して計算されます。論文「Attention Is All You Need」で提示する公式は次の通りです。
- $ P_{(pos,\ 2i)}=sin(\frac{pos}{10000^{2i/d_{model}}}) $
- $ P_{(pos,\ 2i+1)}=cos(\frac{pos}{10000^{2i/d_{model}}}) $
公式を見ると、posは文章における単語の位置を意味し、iはその位置のembeddingを意味します。例を通してこれをより深く説明します。この公式を使用した位置エンコーディング行列を表現すると、次のようになります。

上記の行列で見られるように、位置エンコーディングでiの値が偶数の場合はsin関数を、iの値が奇数の場合はcos関数を使用します。この行列を簡単に表現すると次のようになります。

入力文で単語「I」は0番目の位置、「am」は1番目の位置、「good」は2番目の位置です。pos値を位置情報に置き換えると、次のように表現できます。

最終的にこれを計算すると、位置エンコーディング行列Pは次のような値を持ちます。

ここまでが下図で赤く表示されたEncoderに入力されるまでの過程でした。

それでは位置エンコーディングについて説明しましたので、またEncoderに戻り、2番目のサブレイヤであるFeed-Forward Neural Networkについてお話しします。
1番目のサブレイヤはMulti-head Attentionです。
Position-wise Feed-Forward Neural Network
Position-wise FFNNはTransformerのEncoderとDecoderで持つサブレイヤーです。Multi-head Attentionを通じて得られた各Headは、自分の観点によって情報が偏っているため、Position-wise FFNNは各Headが作り出したAttentionを偏らないよう均等に混ぜる役割を果たします。
Multi-head Attentionの結果として得られた行列xに対するPosition-wise FFNNの数式は次のとおりです。
- $ FFNN(x) = MAX(0, x{W_{1}} + b_{1}){W_2} + b_2 $
Multi-head Attention行列の結果は、Encoderの入力だった入力行列のサイズ$(\text{seq_len},\ d_{model})$と同じです。この例で使用されるseq_lenは、「I am good」の3、embedding次元は512だったため、(3, 512)サイズの行列です。
上記の数式を簡単に図で表現すると、次のようになります。

ここでweight matrix$W_{1}$は$(d_{model},\ d_{ff})$のサイズを持ち、weight matrix$W_{2}$は$(d_{ff},\ d_{model})$のサイズを持ちます。論文では$d_{ff}$を2,048に定義します。このパラメータ($W_{1}, b_{1}, W_{2}, b_{2}$)は、同じEncoder層内では異なる文章、異なる単語ごとに正確に同じ値で使用されますが、Encoder層ごとに異なる値を持ちます。
残差接続とレイヤー正規化
Transformerでは、2つのサブレイヤーを持つEncoderとDecoderに追加で使用する手法があります。Add&Normですが、AddとNormの要素は基本的に残差接続(Residual Connection)とレイヤー正規化(Layer Normalization)です。
残差接続
残差接続の意味を理解するために、ある関数$H(x)$について話します。
- $H(x)=x+F(x)$
この式は、入力$x$と$x$に対するある関数$F(x)$の値を加えた関数$H(x)$の式を示します。ある関数F(x)がTransformerではサブレイヤーに該当します。つまり、残差接続はサブレイヤーの入力と出力を加えることを意味します。Transformerのサブレイヤーの入力と出力は同じ次元を持っているので、サブレイヤーの入力と出力は足し算ができます。残差接続は、画像処理分野で使用されるモデルの学習を支援する手法です。
これを式で表現すると$x+Sub\ Layer(x)$になります。
例えば、サブレイヤーがMulti-head Attentionであれば、残差接続演算は次のようになります。
- $H(x) = x+Multi$-$head\ Attention(x)$
残差接続のより詳しい説明については、以下の論文を參考してください。
レイヤー正規化
残差接続を経た結果は、引き続きレイヤー正規化プロセスを経ることになります。残差接続の入力を$x$、残差接続とレイヤー正規化の2つの演算をすべて行った後の結果値行列を$LN$としたとき、残差接続後のレイヤー正規化演算を数式で表現すると次のようになります。
- $LN = LayerNorm(x+Sub\ Layer(x))$
続いて、レイヤー正規化プロセスについて説明します。レイヤー正規化は、テンソルの最後の次元に対して平均と分散を求め、値を正規化することで学習するために利用されます。ここでテンソルの最後の次元とは、Transformerでは$d_{model}$次元を意味します。
下の図は、レイヤー正規化プロセスを表現した図です。ここで矢印は$d_{model}$次元の方向を意味します。

この行列が (seq_len, $d_{model}$) としたとき(3, 4) の行列になります。
レイヤー正規化のために矢印方向にそれぞれ平均と分散を求めます。そしてレイヤー正規化を実行した後、ベクトル$x_{i}$は$ln_{i}$というベクトルに正規化されます。
- $ln_{i}=LayerNorm(x_{i})$
レイヤー正規化は2つのプロセスに分けられます。1つ目は平均と分散による正規化、2つ目はガンマとベータというベクトルを導入することです。まず、平均と分散によりベクトル$x_{i}$を正規化します。$x_{i}$はベクトルである反面、平均$μ_{i}$と分散$σ^{2} _ {i}$はスカラーです。
ベクトル$x_{i}$の各次元をkとしたとき、$x_{i,k}$は次の数式のように正規化できます。簡単に言えば、ベクトル$x_{i}$の各k次元の値が次の数式のように正規化されるという意味です。
- $\hat{x} _ {i, k}=\frac{x _{i,k} - μ _ {i}}{\sqrt{σ^{2} _ {i}+\epsilon}}$
$ϵ$は分母がゼロになるのを防ぐ値です。次は$γ$(ガンマ)と$β$(ベータ)というベクトルを用意します。ただし、これらの初期値は1と0です。

$γ$と$β$を導入したレイヤー正規化の最終数式は次のとおりであり、$γ$と$β$は学習可能なパラメータです。
- $ln_{i}=γ\hat{x}_{i}+β=LayerNorm(x _{i})$
レイヤー正規化も残差接続と同様に、別の論文があります。レイヤー正規化に関するより詳細な説明については、以下の論文を参考してください。
ここまでがEncoderのすべての構成要素に対する説明でした。最後に、Encoderの構成要素をすべて総合してEncoderが全体的にどのように動作するかで仕上げにします。
Encoder構成要素の統合
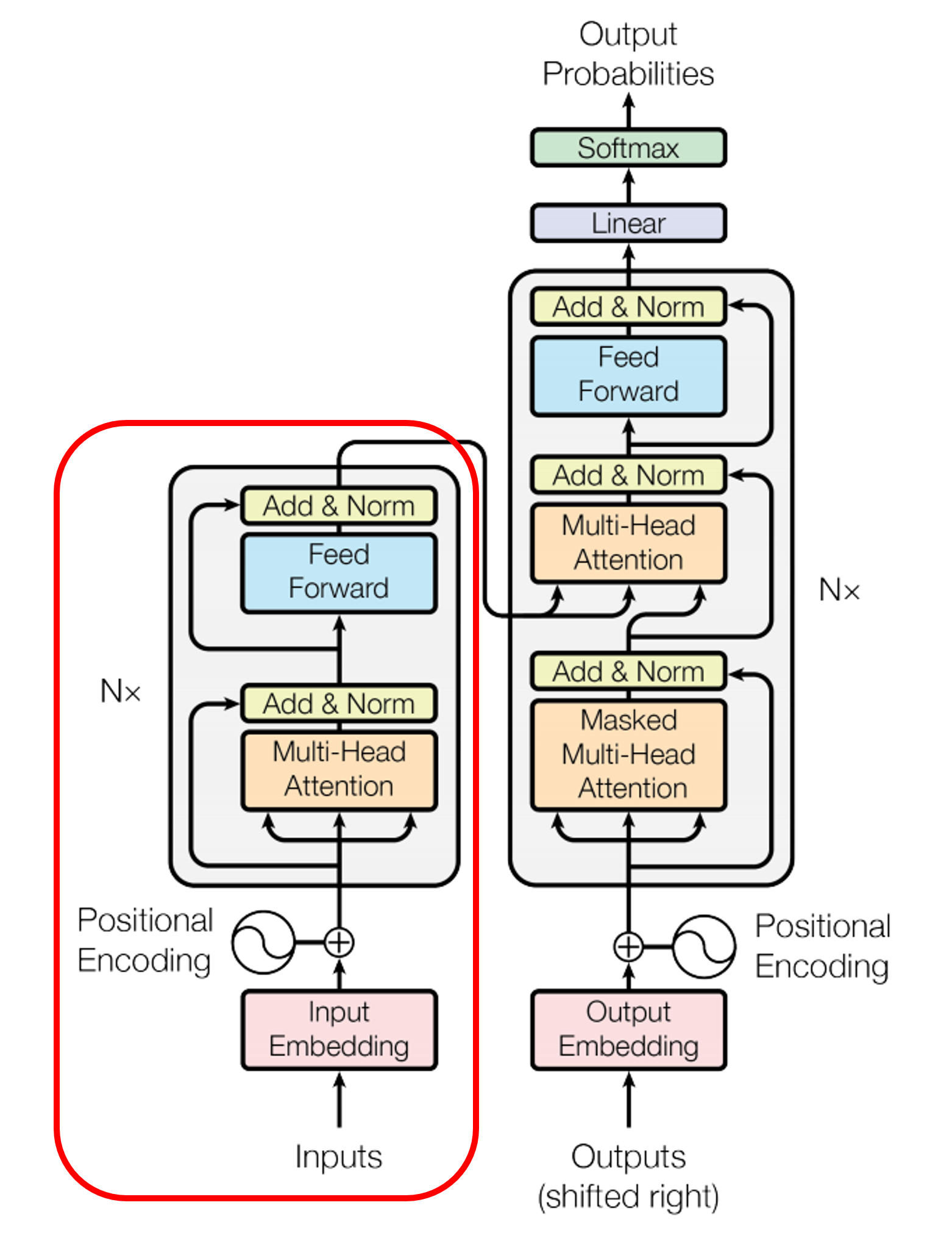
上の図で赤い部分は今まで説明したEncoderの構成要素です。5段階でEncoderのプロセスを要約します。
- 文章を入力行列(embedding行列)に変換した後、位置エンコーディングを追加し、一番下にあるEncoder(Encoder 1)に入力値として提供する。
- Encoder 1は入力値を受け取り、Multi-head Attentionのサブレイヤーに値を送り、Attention行列を結果値として出力する。
- Attention行列を次のサブレイヤーであるFeed-Forward Neural Networkに入力する。Attention行列を入力値として受け取り、レイヤー正規化を経た後、Encoder表現を結果値として出力する。
- Encoder 1の出力値をその上にあるEncoder 2に入力値として提供する。
- Encoder 2は前と同じプロセスを行い、Encoder表現結果を出力として提供する。
Encoderは全部でN個が使われ、最上位Encoderの出力値はEncoderの表現値になります。このように生成された最終Encoderの表現をRといいます。最終Encoderから得られたRは、Decoderの入力値に入ります。DecoderはEncoder表現(R)を入力値として使用し、ターゲット文章(ここでは翻訳先の文章)を生成します。
今までTransformerのEncoderを説明しました。次の記事ではTransformerのDecoderについて書きます。 Decoder編は以下を参照してください。
もしこの記事に間違った部分やぎこちない部分があれば、いつでも連絡お願いします!
