LoginSignup
18
18

More than 5 years have passed since last update.

@makito

Rを使って漫画家東村アキコの作品を分析する話 - まずは主成分分析から

Last updated at Posted at 2015-05-13

こんにちは自称計量東村アキコ学第一人者の @makito です。

さて、計量東村アキコ学では、骨の折れるセリフのデータ化作業をこなしつつ、データ更新の後にExcelでデータを集計してWekaで分析をかけ、Excelでグラフを作って、という作業を繰り返すのが苦痛になり、自動化を試みることにしました。データ分析にはRが非常に便利らしいので調べ始めました。

ひまわりっ

東村アキコ先生の↑の「ひまわりっ」はセリフ数多すぎです。もっと、少女マンガ的にざくっと巨大な絵にセリフは一言「こんにちは」ぐらいを希望します。釣りバカ日誌的な細かいコマ割と、ギャグ漫画ゆえのセリフの多さ…

:round_pushpin: はじめに結論

色々と調べつつ書いているうちに、Rと主成分分析関係に興味があるなら

  • @hoxo_m さんのブログを読む
  • :book: アート・オブ・R・プログラミング
  • ググる

のが良いと感じました。以下の続きの文章はそこに至るまでの道のりでございます。

:cupid: Rとの出会い

実は、 @kaz-yos さんが書かれた R - データ分析系研究者のためのgitによるバージョン管理 - Qiita の

2014年は研究の再現性ということが非常に話題になった年だったと思います。

という冒頭のくだりにハート :cupid: を射止められました。統計解析とプログラミング界隈全体を俯瞰した比較調査はしてません。Rが最適かわかりませんが、Javascript+Excel+Wekaよりは良いことを期待しています(このパラグラフはこの絵文字 :cupid: のために書きました)。

この投稿は適当なものが続きます。できるだけ、Rと主成分分析の話を中心にまとめますが、緩い感じで読んでください。

ところで、「R」が何を指しているのかイマイチわかっていません。プログラミング言語はR言語というのでしょうか？Rだけで通じるのかな？統計の世界ではRと言えば相関係数ですね。何か命名の由来に関係がありそうですが… （いけません、脱線しました :anger:）

:punch: 最初のつまづき

Rを始めたものの、ベクトル、リスト、データフレームに慣れません。それぞれが内部的にどんな状態になっているのか知る方法もよくわからず、困ってます。Javascriptで言うところの console.log(someobject) 的に、とりあえずメソッド名からプロパティ名まで全部出す方法は無いのでしょうか？

知りうる範囲のプログラミング言語的な観点からこの3つを説明すると

  • ベクトルは配列っぽい
  • リストはハッシュオブジェクトっぽい（名前で引ける）
  • データフレームは意味不明だけど、何らかの分析するときはこの形で関数に渡すことが多そう

という感じです。何度かサンプルをこなして、「こういう時には○○を使う」がつかめるまで苦労しそうです。例えば、Rで主成分分析を行う関数の戻り値はデータフレームの形式なのか？とかその辺からつまづきました。

prcomp returns a list with class "prcomp" containing the following components:

R: Principal Components Analysis

マニュアルにはprcomp()の戻り値はリストのようです。例えば、リストlstの個々の成分cにアクセスして、cのデータ型を返す方法は

  • lst$c
  • lst[["c"]]
  • lst[[i]]　(iはlst内のcのインデックス ※1から開始される整数)

という3つがあります。（何故二重カッコなのですか？）

pca = prcomp(data)
pca$x

といった感じで、主成分のスコアを出力できるのは、なるほど納得できました。RにおいてリストはJavascriptのオブジェクトのような使い方をするのが良さそうです。

と、そんなことを考えていたら :book: アート・オブ・R・プログラミングの4章「リスト」の冒頭に以下の記述がありました。

すべての要素が同じモードでなければいけないベクトルとは対照的に、Rのlist構造はさまざまな種類のオブジェクトを結合できます。Pythonを使い慣れた人なら、RのリストはPythonのディクショナリに似ており、さらに言えばPerlのハッシュに似ていると思うでしょう。CプログラマはCの構造体に似ていると感じるでしょう。リストはRで中心的な役割を果たし、データフレーム、オブジェクト指向プログラミングなどの基礎となります。

どうやら、ハッシュオブジェクト的なものだと思ってよさそうです。

:book: アート・オブ・R・プログラミング

ちなみに、Rの記事を良く投稿されているアマ○ンみたいなロゴの @hoxo_m さんが、ブログ記事で :book: アート・オブ・R・プログラミングについて

プログラミング初心者向けではないですが、他の言語になじんでる人が R に入門したい場合には、他の入門書よりもこっちを読んだ方が手っ取り早いのではないかと思います。

統計言語 R の公式ヘルプでさらっと目を通しておくと良いトピックまとめ - ほくそ笑む - http://goo.gl/sLIW2

と紹介されています。実際その通りだと思います。

:wrench: Rと主成分分析

もしかしたら、この投稿はRの初心者の方が読んでいるかもしれません。もしRに取り組み始めた理由が主成分分析に関係していたら同じような悩みを解決する手助けになるかもしれません。そんな感じで書いています。

主成分分析の特徴

これまで計量東村アキコ学で書いた

これらの記事では、キャラクターのセリフを統計的に分析する際に主成分分析を使ってきました。セリフ末尾の記号使用回数や、品詞の使用頻度という量的データを使い「マンガに登場するキャラクターをどのように書き分けているのか？」という好奇心を満たそうという試みでもあります。そこにデータがあると思わず何かいじってみたくなりませんか？（いけません、脱線しました :anger:）

時々、主成分分析の特徴の一つに「次元を落とす」ことが挙げられていることがあります。三次元を超えるデータを視覚的に認識するのが苦手なので、二次元ぐらいに落としてもらえると助かります。

例えば、主成分分析の特徴を次のように解説しているひともいます。

主成分分析(Principal Component Analysis, PCA)とは、

  1. データの無相関化
  2. データの次元の削減 を行う手法です。 簡単に言うと、データを分析しやすいように再構成し、可能なら次元を下げることです。

Pythonで主成分分析 - old school magic - http://goo.gl/pFeKdV

興味深い主成分分析にまつわる話

やりたいことは、どちらかとえいば、数式をいじったり分析方法の正確性を議論するよりも、 データを集めて何かわからないでしょうか？ という好奇心の方が大きいので、 つまりは主成分分析とは？ に近づける話にとても興味があります。

ネット上に面白いページがありましたので紹介します。

（おまけ） 早わかり　主成分分析

例えば、

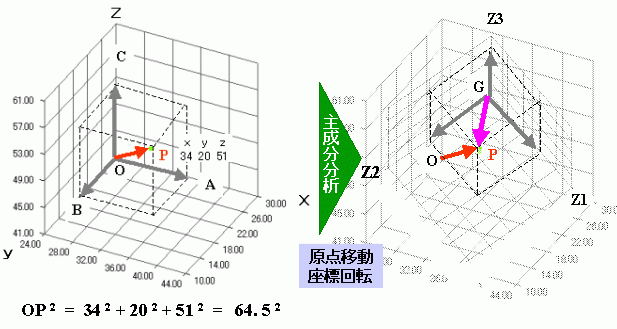
主成分分析は次元を落とすツールです

ということが図付きで分かり易く解説されていたり

image

図３．主成分分析で軸を回転させたイメージ図

次世代の主成分分析の利用法とは

として、

メカニズム提示
同時に算出されてくる因子負荷量（主成分負荷量という人もいる）を手がかりにして、実測さ れる変数間の因果関係（メカニズム）を抽出できます。

メカニズムの分離
数種のメカニズムが混合している場合に、メカニズムも個別に分離してくれます。

変数選択
あるメカニズムに関係のない変数と関係のある変数をよりわけることができます。

データマイニング指針提示
層別データとか分類型のデータはカテゴリカルデータと呼ばれています。主成分分析にカテゴ リカルデータを取り入れると、多くの変数の中から層別すべきカテゴリカル変数だけを選択し てくれます。

と書いてあります。すでに統計分析に詳しい人には当たり前の話なのかもしれませんが…

:question: 主成分分析に使える prcomp() と princomp() の違いは？

Rで主成分分析ができる関数には prcomp() と princomp() があります。各所の解説ではどちらも使われていて、違いがよくわかりません。いろいろ調べましたが、未だに完全に理解したわけではなく、それでも、調べたことをまとめます。

Rには主成分分析を行うためにprcomp()とprincomp()という2つの関数が用意されている。どちらも大きな違いはないが、prcomp()はサンプルサイズが変数の数よりも少ない場合にも適用できる、という利点をもっている。また、prcomp()は計算時に不偏分散を用いるのに対して、princomp()では標本分散を用いている。両者に若干の違いはあるが、基本的にはどちらを使っても構わないだろう。

引用元： http://homepage2.nifty.com/nandemoarchive/GLM/tahenryou_02_PCA.htm

「どちらを使っても構わない」 のですか、困ります。不偏分散と標本分散の違い主成分分析の結果にどんな違いが出るのでしょうか？

マニュアルにはprcompの方が数値特性が優れていると書かれているので、ここではprcomp関数を紹介します。

引用元：オライリーのRクックブック p.279

「数値特性が優れている」 とはどういうことでしょうか？引用の引用になってしまいました。いつか、マニュアルを見る必要がありあそうです。

結局よくわからないままです。 @hoxo_m さんのブログにも解説記事がありました。

統計解析でよく使われる言葉「Qモード」「Rモード」とは何を指すのか - ほくそ笑む - http://goo.gl/2DTpg

謎コードに見えるけど・・・

しかしコードとして良くわからないのが biplot() 関数に prcomp() と princomp() どちらの戻り値を使用しても散布図が描画される点です。どうなっているのでしょうか？少なくとも、散布図描画に使用されるデータは prcomp() の場合は 


pca = prcomp(data)
pca$x

pca$x ですし、princomp() の場合は


pca = prcomp(data)
pca$scores

pca$scores にあります。関数 biplot() が内部的にどちらの引数でも対応できるように実装されているのでしょうか？biplot()の実装をみると


biplot <- function(x, ...) UseMethod("biplot")

biplot.default <-
    function(x, y, var.axes = TRUE, col, cex = rep(par("cex"), 2),
         xlabs = NULL, ylabs = NULL, expand=1, xlim = NULL, ylim = NULL,
         arrow.len = 0.1,
             main = NULL, sub = NULL, xlab = NULL, ylab = NULL, ...)
{
    n <- nrow(x)
    p <- nrow(y)
    if(missing(xlabs)) {
    xlabs <- dimnames(x)[[1L]]
# 省略
}

biplot.princomp <- function(x, choices = 1L:2L, scale = 1, pc.biplot=FALSE, ...)
{
    if(length(choices) != 2L) stop("length of choices must be 2")
    if(!length(scores <- x$scores))
    stop(gettextf("object '%s' has no scores", deparse(substitute(x))),
             domain = NA)
    lam <- x$sdev[choices]
    if(is.null(n <- x$n.obs)) n <- 1
    lam <- lam * sqrt(n)
    if(scale < 0 || scale > 1) warning("'scale' is outside [0, 1]")
    if(scale != 0) lam <- lam^scale else lam <- 1
    if(pc.biplot) lam <- lam / sqrt(n)
    biplot.default(t(t(scores[, choices]) / lam),
           t(t(x$loadings[, choices]) * lam), ...)
    invisible()
}

biplot.prcomp <- function(x, choices = 1L:2L, scale = 1, pc.biplot=FALSE, ...)
{
    if(length(choices) != 2L) stop("length of choices must be 2")
    if(!length(scores <- x$x))
    stop(gettextf("object '%s' has no scores", deparse(substitute(x))),
             domain = NA)
    if(is.complex(scores))
        stop("biplots are not defined for complex PCA")
    lam <- x$sdev[choices]
    n <- NROW(scores)
    lam <- lam * sqrt(n)
    if(scale < 0 || scale > 1) warning("'scale' is outside [0, 1]")
    if(scale != 0) lam <- lam^scale else lam <- 1
    if(pc.biplot) lam <- lam / sqrt(n)
    biplot.default(t(t(scores[, choices]) / lam),
           t(t(x$rotation[, choices]) * lam), ...)
    invisible()
}

となっていて、biplot.prcomp, biplot.princomp関数が定義されています。こういうことが気になってしまう時には、「:book: アート・オブ・R・プログラミング」をオススメします。言語的な面からRの理解が進む大事なことが色々書いてあります。

R: Principal Components Analysis prcomp() - https://goo.gl/8CXVU0
R: Principal Components Analysis princomp() - https://goo.gl/Wiowpe
R: Biplot of Multivariate Data - https://goo.gl/6mYq2e

また、このあたりのことは、Rのオブジェクト指向とかポリモーフィズムとかでググって調べると情報が見つかるかもしれません。

Mirror House Lab: Rでオブジェクト指向 (S3) - http://goo.gl/2AML3q

:wrench: 使用するツール RStudio が素晴らしすぎる :cry:

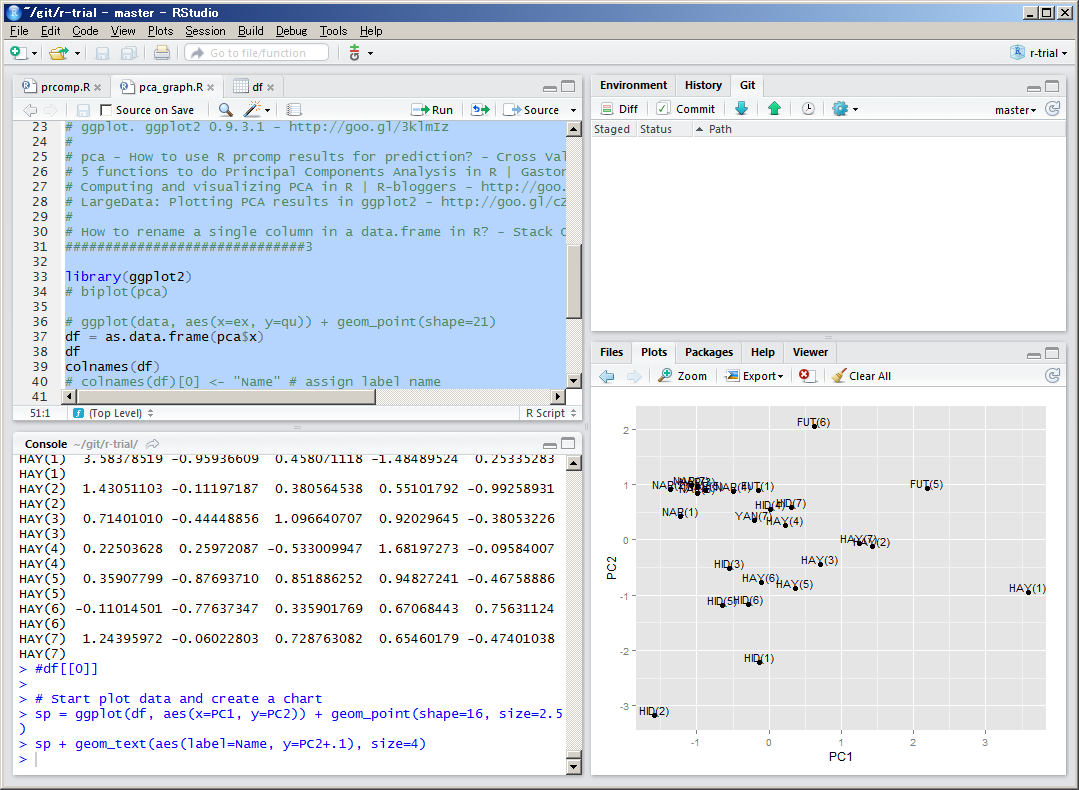
Rを使うにはRStudioが便利です。とても良いです。データが見えるようになるのでデバッグしやすいし、ベクトル、リスト、データフレームといったR独自の考え方に慣れない間は助けられることが多いです。さらに、git/svn といったバージョン管理システムと容易に連携できます。

RStudioのウィンドウ

これはRStudioのウィンドウです。プログラミングに使用するIDEのような感じで使います。

  • git との連携
  • スクリプト中の変数の可視化
  • グラフの画像保存、クリップボード化が後から可能
  • グラフの履歴保持
  • CRANというパッケージ管理システム

この辺が特に素晴らしいと思っております。

:heart: おまけ

データの可視化（ビジュアライジング）について

"Visualizaing Data" (邦訳『ビジュアライジング・データ』) で紹介されていた、データ可視化の7ステージ(The Seven Stages of Visualizing Data)。分析に手を付ける前に思い出すと、スムーズに課題を整理できる。でも、出てきた課題をそれぞれどう解決するかは別の話。

  1. Acquire: データを手に入れる。
  2. Parse: 生のデータを構造化する。
  3. Filter: 不要なデータを取り除く。
  4. Mine: 統計・マイニング手法を適用する。
  5. Represent: 基本的な可視化モデル（棒グラフ、散布図、ツリーなど）で表現する。
  6. Refine: 基本的な可視化モデルを洗練させる。
  7. Interact: 可視化モデルを操作できるようにする。

Mirror House Lab: データ可視化の7ステージ - http://goo.gl/zLGFH5

18
18
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
18
18