LoginSignup
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@makinono(ま きの)

Skyfieldで惑星の位置を計算してStreamlitで可視化してみた

Posted at

はじめに

Pythonでアプリ作り100日チャレンジの58日目です。
現在「星のソムリエ®」講座を受講中で、学習の復習を兼ねてPythonで惑星の現在地を可視化するアプリを作りました。天体計算ライブラリの Skyfield と Streamlit を使用しました。
数学が苦手なので実装中に滅茶苦茶悩んだポイントとその解決策の学習記録です。

作ったもの

本記事で紹介したアプリは、学習目的で GitHub に公開しています。
天体計算や可視化の参考になれば幸いです。
https://github.com/MikiMakino/100days-of-code/tree/main/day58-planet-position

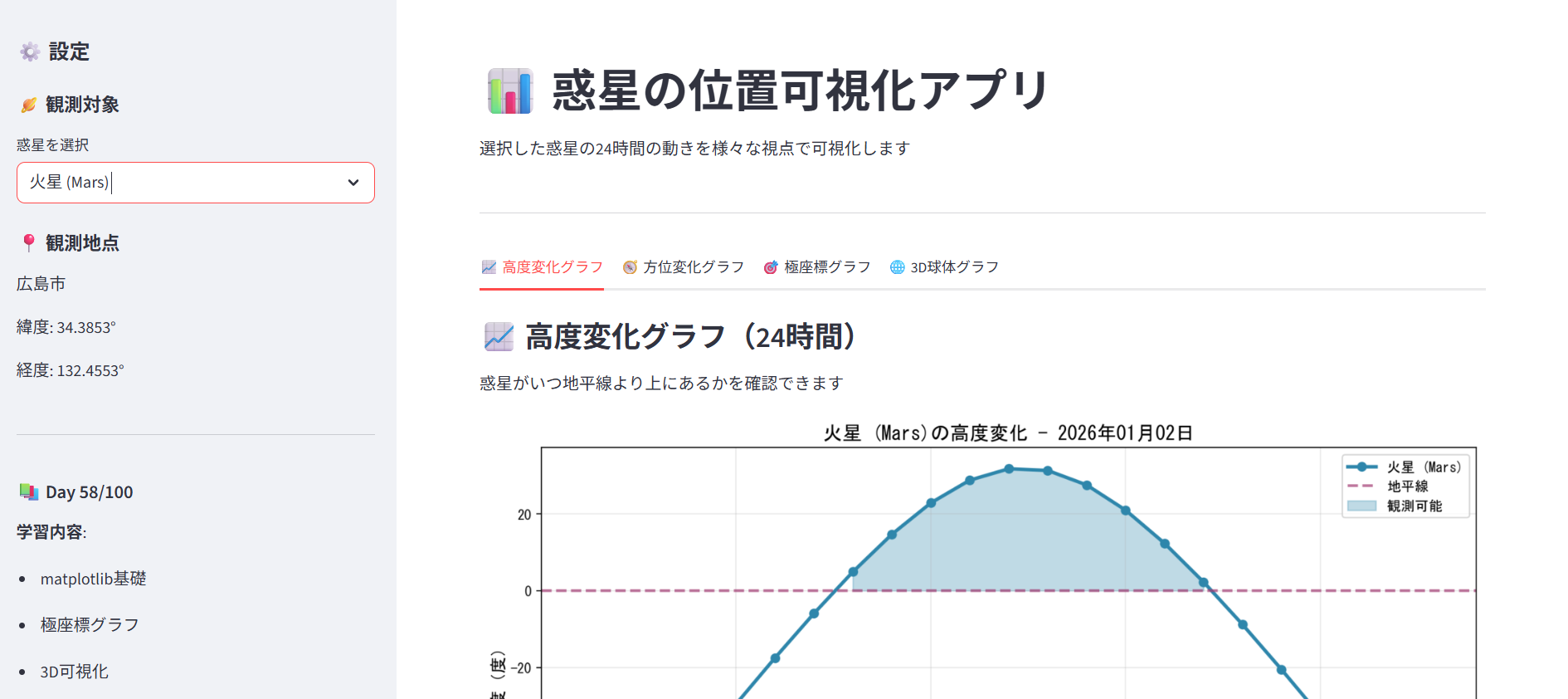
image.png

惑星（火星など）の24時間の動きを算出し、以下の4つの視点で可視化しました：

  • 高度・方位グラフ：時間経過に伴う惑星の高度と方位角の変化
  • 極座標グラフ：実際のコンパスのように北を上にした平面図
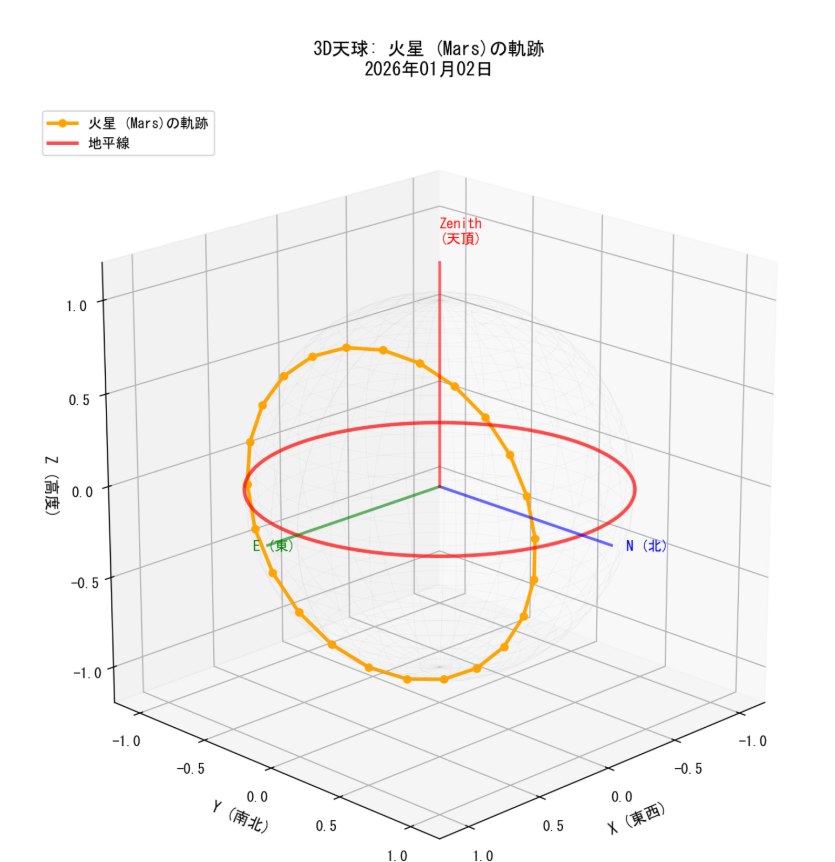
  • 3D天球モデル：観測者を中心とした立体的な天球
  • 数値テーブル：詳細な計算結果

ポイント1：計算結果が9時間ずれる（JSTとUTCの問題）

問題

グラフの時刻表示が実際の時刻から9時間ずれてしまいました。

原因

Skyfieldの計算基準はUTCです。
Python標準の datetime をそのまま渡すと、結果が9時間ずれてしまいます。

解決策

timezone を明示して、
Skyfieldに+9時間と定義する必要があります。

from datetime import datetime, timedelta, timezone

JST = timezone(timedelta(hours=9))
now = datetime.now(JST)    # ユーザーが見る時のJST
t = ts.from_datetime(now)  # これで内部的には正しいUTCに変換される

ポイント：Skyfieldは datetime オブジェクトのタイムゾーン情報を見て、自動的にUTCに変換してくれます。

ポイント2：3D座標変換で「右と左が逆」になる

問題

球面座標（高度・方位角）から直交座標（x, y, z）に変換する際、
惑星の配置が実際の空の見え方と一致せず、分からなくなりました。

原因

数学の基本座標は「右が $0°$」ですが、天文学の方位は「上が $0°$（北）」です。

解決策

数学的に解決するために、 $x$ と $y$ の三角関数を入れ替えて実装しました。

# 高度と方位角から3D座標を計算
alt_rad = np.radians(alt)
az_rad = np.radians(az)

# 高さ（Z軸）
z = np.sin(alt_rad)

# 水平面での半径
r = np.cos(alt_rad)

# 数学の基本（x=cos, y=sin）をあえて逆にする
x = r * np.sin(az_rad)  # 北(0°)のとき左右のズレを0にする
y = r * np.cos(az_rad)  # 北(0°)のとき上(奥)の値を最大にする

この工夫により、「北を向いて空を見上げた時、右（東）から星が昇り、正面（北）を通る」という現実の動きと完全に一致させることができました。

補足：球面座標の考え方

天体の位置を3D空間で表現する際、天球モデルという考え方を使います：

  • Z軸：高度（天頂方向）→ z = sin(alt)
  • r（水平半径）：天体が地平線からどれだけ離れているかを表す「横方向の広がり」→ r = cos(alt)
  • X, Y軸：方位角から計算される水平面上の位置

高度が高い（天頂に近い）ほど
cos(alt) が小さくなり、r は小さくなります。
天体は天球の中心付近に描かれます。

高度が低い（地平線に近い）ほど、
天体は天球の縁に描かれます。

処理の高速化：@st.cache_resource の活用

NASAの天体暦データ（de421.bsp）は非常に精密ですが、ファイルサイズが約17MBと大きいため、毎回読み込むとアプリが重くなります。

Streamlitの @st.cache_resource を使ってメモリに一度だけ読み込ませることで、サクサク動く操作感を実現しました。

from skyfield.api import load

@st.cache_resource
def load_ephemeris():
    """天体暦データを読み込む（初回のみ実行）"""
    return load('de421.bsp')

@st.cache_data
def calculate_planet_data(planet_name, lat, lon, date_str):
    """惑星データを計算する（パラメータが変わったときのみ実行）"""
    # 計算処理...
    return altitudes, azimuths

キャッシングのポイント：

  • @st.cache_resource：変わらないリソース（天体暦ファイル）に使用
  • @st.cache_data：条件で変わる計算結果（惑星や日付によって変化）に使用

これにより、24時間分の天体計算という重い処理も快適に実行できるようになりました。

Skyfieldの基本的な使い方

天体暦データの読み込み

from skyfield.api import load, wgs84

planets = load('de421.bsp')  # NASA JPLの惑星位置データ（1900〜2050年）
earth = planets['earth']
ts = load.timescale()

de421.bsp は、NASAのジェット推進研究所（JPL）が計算した1900年から2050年までの惑星の位置データです。

観測地点の設定（広島）

location = earth + wgs84.latlon(34.3853, 132.4553)

earth + wgs84.latlon は、単なる緯度経度ではなく、地球の楕円体モデル（WGS84）上の正確な地点を表します。

  • WGS84：「世界測地系1984」の略で、GPSでも使われている世界標準の測地系
  • earth +：太陽系の中心から見た地球上の広島に立っている自分を、宇宙的なベクトルとして定義

つまり、「少し歪んだ地球の表面に立っている自分」を正確に表現しているのです！

惑星を観測する

planet = planets['mars']
astrometric = location.at(t).observe(planet)
alt, az, distance = astrometric.apparent().altaz()
  • observe()：観測者から見た天体の位置を計算
  • apparent()：光の到達時間や視位置（見かけの位置）を考慮
  • altaz()：地平座標系（高度・方位角）で返す

地平座標系（Alt-Az）とは

  • 高度（Altitude）：地平線を $0°$、天頂を $+90°$、地面下を $-90°$ とする角度
  • 方位角（Azimuth）：北を $0°$ として、東回りに $360°$ まで測る角度

※ Skyfieldの alt / az は Angle オブジェクトなので、使用時は .degrees を参照します。

Matplotlibによる可視化

極座標グラフ

実際のコンパスと一致する空の見え方を表現するため、以下のように設定しました：

ax = plt.subplot(111, projection='polar')
ax.set_theta_zero_location('N')  # 北を0°に
ax.set_theta_direction(-1)        # 時計回りに設定

3Dワイヤーフレーム

from mpl_toolkits.mplot3d import Axes3D

# 球体を生成
u = np.linspace(0, 2 * np.pi, 100)
v = np.linspace(0, np.pi, 100)
x_sphere = np.outer(np.cos(u), np.sin(v))
y_sphere = np.outer(np.sin(u), np.sin(v))
z_sphere = np.outer(np.ones(np.size(u)), np.cos(v))

# 天球を描画
ax.plot_wireframe(x_sphere, y_sphere, z_sphere, alpha=0.1)

np.outer を使って球体を生成し、Skyfieldで計算した惑星位置を天球上に重ねて描画しています。

image.png

まとめ

惑星の動きが直感的に理解できました。

参考資料

0
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?