はじめに
政府統計の総合窓口 e-stat を利用し、統計データを分析してみました。
本記事では、2016年と2023年のブロッコリー価格に注目し、統計的手法を活用して価格の変化を検証します。
今回の目的は以下の通りです:
- e-statのデータをPythonで読み込み、加工・可視化する。
- 基本的な統計分析と検定を実施する。
- 具体的には、シャピロウィルク検定、マン・ホイットニーU検定、KS検定を行います。
今回は、小売データのデータを加工して分析を行います。
出典:政府統計の総合窓口(e-Stat)(https://www.e-stat.go.jp/)
モチベーション
私は11月の中旬に統計検定準1級の受験に挑戦しましたが、合格できませんでした。
その背景としては、用語や公式の暗記が先行し、実務での統計分析経験が不足していたことが挙げられると感じました。
そこで、e-statのデータを使って統計分析の実践を行い、統計検定の基礎を再確認することにしました。
本データの特徴
本データは、月ごとのブロッコリーの価格と地域別の価格を示しています。
分析の際に利用したコードはこちらです:basic-usage-of-e-stat/src/2024-11-19-basic.ipynb at main · makinzm/basic-usage-of-e-stat
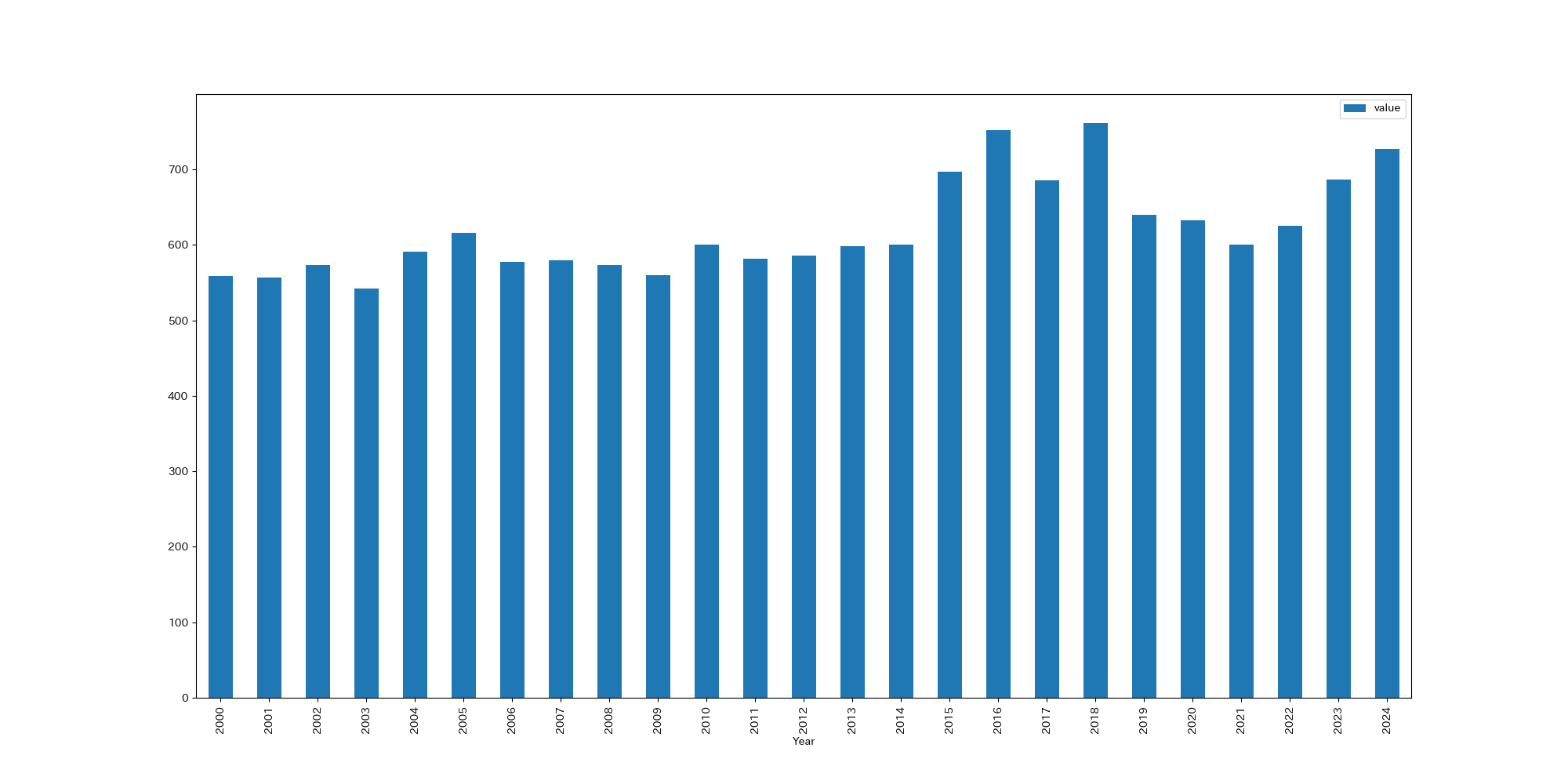
今回は、地域の差分は考慮せず、年ごとの価格変化に注目します。
実際に月及び年ごとの分布を確認したところ、以下のような分布を得ました:
検証する仮説
コロナ禍の前後で食品価格に変化があるかどうかを検証するため、
2016年と2023年のブロッコリー価格には差があるかどうかを検証します。
データ加工と可視化
取得したデータをPythonで読み込み、必要な部分を抽出します。データ加工には以下のライブラリを使用しました:
- pandas: データフレーム操作
- matplotlib: グラフ描画
- scipy: 統計検定
2016年と2023年の比較
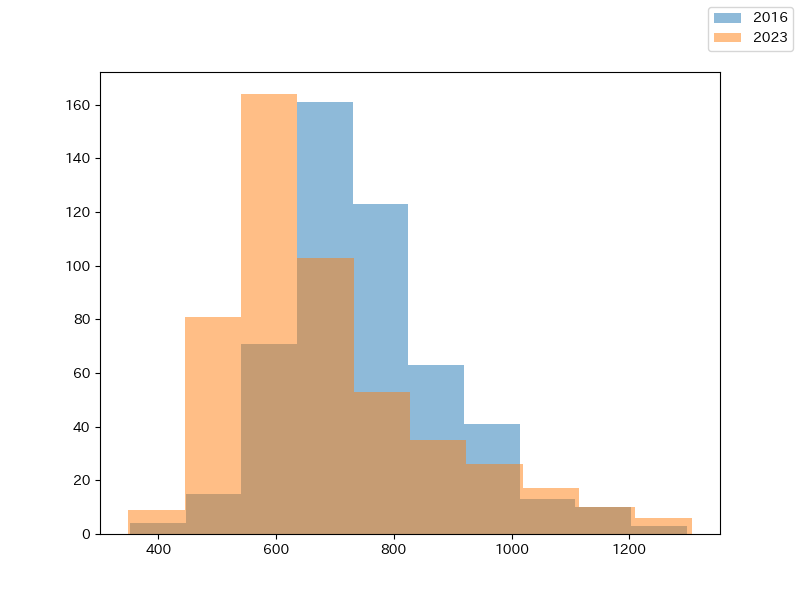
分布の視覚化
2016年と2023年の価格分布を比較した結果が以下のヒストグラムです:
統計検定
正規性の検定
目的:正規分布に従う場合、t検定が有効であるため、正規性を検証します。
-
shapiro — SciPy v1.14.1 Manual
- 統計検定準1級の範囲外ですが、非正規性を確認するために使用します。対立仮説は「正規分布に従わない」です。
シャピロ・ウィルク検定を実施した結果:
- 2016年: p値=3.6e-09 (正規分布ではない)
- 2023年: p値=5.9e-17 (正規分布ではない)
よって、正規性を仮定せずにノンパラメトリック検定を行います。
from scipy.stats import shapiro
# シャピロ・ウィルク検定
stat_2016, p_2016 = shapiro(data_2016)
stat_2023, p_2023 = shapiro(data_2023)
print(f"2016年のシャピロ・ウィルク検定: 統計量={stat_2016}, p値={p_2016}")
print(f"2023年のシャピロ・ウィルク検定: 統計量={stat_2023}, p値={p_2023}")
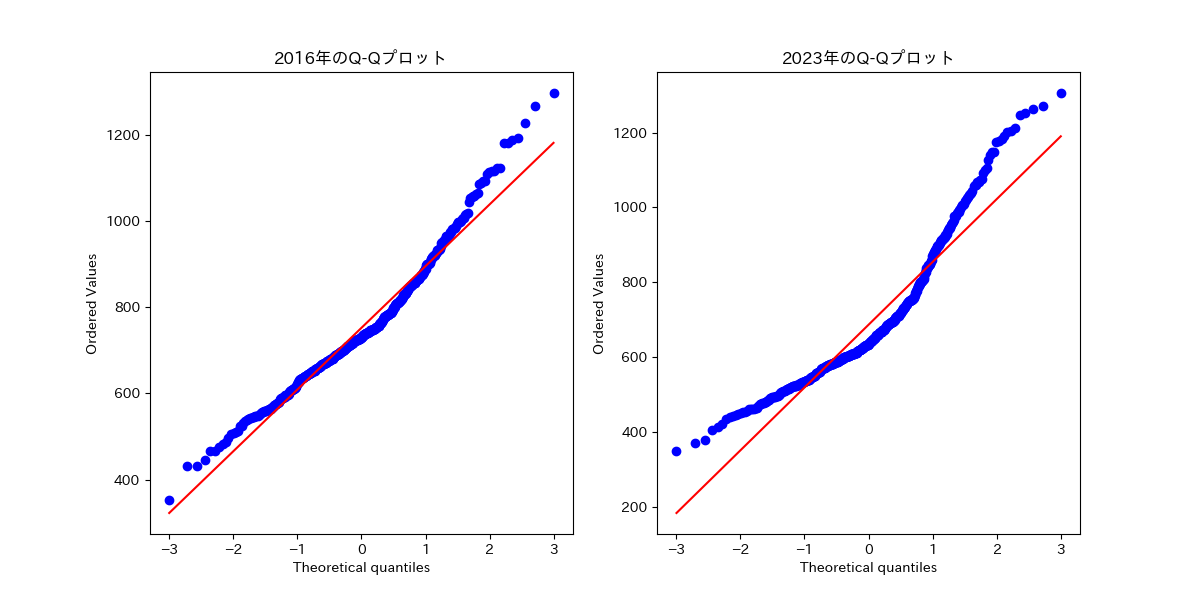
また、Q-Qプロットを行った際も、正規分布に従わないことが確認されました。
import matplotlib.pyplot as plt
import japanize_matplotlib
plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
stats.probplot(data_2016, dist="norm", plot=plt)
plt.title('2016年のQ-Qプロット')
plt.subplot(1, 2, 2)
stats.probplot(data_2023, dist="norm", plot=plt)
plt.title('2023年のQ-Qプロット')
plt.show()
マン・ホイットニーU検定(ウィルコクソンの順位和検定)
目的:分布の中央値が異なる場合は、価格に差があると判断できるため、中央値の差を検証します。
-
mannwhitneyu — SciPy v1.14.1 Manual
- 統計検定準1級では、ウィルコクソンの順位和検定として知られていますが、マン・ホイットニーU検定とも呼ばれます。
マン・ホイットニーU検定(ウィルコクソンの順位和検定)を実施し、2016年と2023年の価格分布に有意差があるかを検証します。
結果は以下の通りです:
- U統計量: 167231.5
- p値: 3.2e-18
from scipy.stats import mannwhitneyu
# マン・ホイットニーU検定
u_stat, p_value_mw = mannwhitneyu(data_2016, data_2023, alternative="two-sided")
print(f"マン・ホイットニーU検定: U統計量={u_stat}, p値={p_value_mw}")
結論:p値が有意水準(0.05)を下回るため、2016年と2023年の価格分布には有意差があると判断されます。
KS検定
目的:マン・ホイットニーU検定と同様に、価格分布に差があるかを検証します。マン・ホイットニーU検定と異なり、KS検定は分布形状に差があるかを検証します。
-
ks_2samp — SciPy v1.14.1 Manual
- 統計検定準1級では範囲外ですが、非パラメトリック検定の一つで対立仮説は「分布形状に差がある」です。
KS検定は、分布形状に差があるかを検証します。
- 統計量: 0.32
- p値: 2.6e-24
結論:p値が有意水準を下回るため、2016年と2023年の分布形状にも有意差があると判断されます。
from scipy.stats import ks_2samp
ks_stat, p_value_ks = ks_2samp(data_2016, data_2023)
print(f"KS検定: 統計量={ks_stat}, p値={p_value_ks}")
考察
統計検定の結果、2016年と2023年でブロッコリー価格には以下の点で違いが見られました:
- 分布の中央値
- 分布の形状
また、どちらの分布も正規分布に従わないため、非パラメトリック検定が適切でt検定は利用できないことを判断し検定を行いました。
おわりに
本記事では、e-statのデータを用いてブロッコリー価格の変化を分析しました。
この実践を通じて、統計検定で扱うような検定(KS検定やシャピロウィルク検定は統計検定準1級の範囲外ですが)を実施し、実際の利用方法や政府統計データの活用方法を学ぶ良い機会となりました。
さらなる理解を深めるために、今後は季節性を考慮した時系列分析や、他の食品価格を踏まえた因果関係の検証などを行っていきたいと考えています。