はじめに
PyTorch 学習メモ (Karasと同じモデルを作ってみた)の続きです。
今度は、同じcifar10を対象として、事前学習済みモデルを利用してモデルを作ってみました。
1. 最終版コード
コードはgithubにあげてあります。URLは下記になります。
実装のポイントになる点は、下記になります。
1.1 データ読み込み
前回は、訓練用・検証用で共通だったtransformerを別々にしています。
そのココロは、訓練用に関して「Data Augmentation」(データ水増し)をすることにあります。
詳細については、2.2 学習データの水増しで説明します。
# transformの定義
# 検証データ用 : 正規化のみ実施
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))
])
# 訓練データ用: 正規化に追加で反転とRandomErasingを実施
transform_train = transforms.Compose([
transforms.RandomHorizontalFlip(p=0.5),
transforms.ToTensor(),
transforms.Normalize([0.5, 0.5, 0.5], [0.5, 0.5, 0.5]),
transforms.RandomErasing(p=0.5, scale=(0.02, 0.33), ratio=(0.3, 3.3), value=0, inplace=False)
])
1.2 モデルの読み込み
モデル読み込みのコードは以下のようになります。
PyTorchでは、事前学習済みモデルが何パターンか用意されていて、これらのモデルは関数を呼び出すだけで重み付きで読み込むことができます。
# 学習済みモデルの読み込み
# Resnet50を重み付きで読み込む
model_ft = models.resnet50(pretrained = True)
# 最終ノードの出力を10に変更する
model_ft.fc = nn.Linear(model_ft.fc.in_features, 10)
# GPUの利用
net = model_ft.to(device)
# 損失関数に交差エントロピーを利用
criterion = nn.CrossEntropyLoss()
# 最適化に関しては、いくつかのパターンを調べた結果、下記が一番結果がよかった
optimizer = optim.SGD(net.parameters(),lr=0.001,momentum=0.9)
具体的に利用可能なモデルは、下記リンク先に一覧があります。
https://pytorch.org/docs/stable/torchvision/models.html
こうしたモデルを利用する場合は、読み込んだ後で、
model_ft.fc = nn.Linear(model_ft.fc.in_features, 10)
のコードで最終段だけ新しいノードに付け替えることで、目的とする分類モデルを作ることが可能です。
ちなみに、このモデルは元々入力サイズが224x224です。このような大きなサイズのモデルにCIFAR-10のような32x32のサイズのデータを突っ込んでいいのかも最初はよくわからなかったのですが、結論として問題はないようです。多分、大量の重みがまったく使われずに無駄になるだけなのだと思います。
逆に、例えば1024x1024のように元のモデルより解像度の大きなデータをモデルに入れる場合は、前処理で、解像度を224x224に落とすことが必要になります。
1.3 モデルの概要表示
モデルの概要表示をしたい場合は、この段階で netを実行すればいいです。
resnet50の場合の結果を、以下に示します。
Bottleneck(
(conv1): Conv2d(512, 256, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv3): Conv2d(256, 1024, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn3): BatchNorm2d(1024, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
(downsample): Sequential(
(0): Conv2d(512, 1024, kernel_size=(1, 1), stride=(2, 2), bias=False)
(1): BatchNorm2d(1024, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
)
(1): Bottleneck(
(conv1): Conv2d(1024, 256, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv3): Conv2d(256, 1024, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn3): BatchNorm2d(1024, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
)
(2): Bottleneck(
(conv1): Conv2d(1024, 256, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv3): Conv2d(256, 1024, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn3): BatchNorm2d(1024, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
)
(3): Bottleneck(
(conv1): Conv2d(1024, 256, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv3): Conv2d(256, 1024, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn3): BatchNorm2d(1024, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
)
(4): Bottleneck(
(conv1): Conv2d(1024, 256, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv3): Conv2d(256, 1024, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn3): BatchNorm2d(1024, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
)
(5): Bottleneck(
(conv1): Conv2d(1024, 256, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv3): Conv2d(256, 1024, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn3): BatchNorm2d(1024, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
)
)
(layer4): Sequential(
(0): Bottleneck(
(conv1): Conv2d(1024, 512, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv2): Conv2d(512, 512, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv3): Conv2d(512, 2048, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn3): BatchNorm2d(2048, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
(downsample): Sequential(
(0): Conv2d(1024, 2048, kernel_size=(1, 1), stride=(2, 2), bias=False)
(1): BatchNorm2d(2048, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
)
(1): Bottleneck(
(conv1): Conv2d(2048, 512, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv2): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv3): Conv2d(512, 2048, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn3): BatchNorm2d(2048, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
)
(2): Bottleneck(
(conv1): Conv2d(2048, 512, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv2): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv3): Conv2d(512, 2048, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn3): BatchNorm2d(2048, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
)
)
(avgpool): AdaptiveAvgPool2d(output_size=(1, 1))
(fc): Linear(in_features=2048, out_features=10, bias=True)
)
さすがに長いですね。相当複雑なニューラルネットであることがわかります。
1.4 モデルのサイズ表示
どの段のノードのサイズがいくつであるか確認するためには、この段階で次のコードを実行します。
# モデルのサマリー表示
from torchsummary import summary
summary(net,(3,128,128))
結果は次のとおりです。
----------------------------------------------------------------
Layer (type) Output Shape Param #
================================================================
Conv2d-1 [-1, 64, 16, 16] 9,408
BatchNorm2d-2 [-1, 64, 16, 16] 128
ReLU-3 [-1, 64, 16, 16] 0
MaxPool2d-4 [-1, 64, 8, 8] 0
Conv2d-5 [-1, 64, 8, 8] 4,096
BatchNorm2d-6 [-1, 64, 8, 8] 128
ReLU-7 [-1, 64, 8, 8] 0
Conv2d-8 [-1, 64, 8, 8] 36,864
BatchNorm2d-9 [-1, 64, 8, 8] 128
ReLU-10 [-1, 64, 8, 8] 0
Conv2d-11 [-1, 256, 8, 8] 16,384
BatchNorm2d-12 [-1, 256, 8, 8] 512
Conv2d-13 [-1, 256, 8, 8] 16,384
BatchNorm2d-14 [-1, 256, 8, 8] 512
ReLU-15 [-1, 256, 8, 8] 0
Bottleneck-16 [-1, 256, 8, 8] 0
Conv2d-17 [-1, 64, 8, 8] 16,384
BatchNorm2d-18 [-1, 64, 8, 8] 128
ReLU-19 [-1, 64, 8, 8] 0
Conv2d-20 [-1, 64, 8, 8] 36,864
BatchNorm2d-21 [-1, 64, 8, 8] 128
ReLU-22 [-1, 64, 8, 8] 0
Conv2d-23 [-1, 256, 8, 8] 16,384
BatchNorm2d-24 [-1, 256, 8, 8] 512
ReLU-25 [-1, 256, 8, 8] 0
Bottleneck-26 [-1, 256, 8, 8] 0
Conv2d-27 [-1, 64, 8, 8] 16,384
BatchNorm2d-28 [-1, 64, 8, 8] 128
ReLU-29 [-1, 64, 8, 8] 0
Conv2d-30 [-1, 64, 8, 8] 36,864
BatchNorm2d-31 [-1, 64, 8, 8] 128
ReLU-32 [-1, 64, 8, 8] 0
Conv2d-33 [-1, 256, 8, 8] 16,384
BatchNorm2d-34 [-1, 256, 8, 8] 512
ReLU-35 [-1, 256, 8, 8] 0
Bottleneck-36 [-1, 256, 8, 8] 0
Conv2d-37 [-1, 128, 8, 8] 32,768
BatchNorm2d-38 [-1, 128, 8, 8] 256
ReLU-39 [-1, 128, 8, 8] 0
Conv2d-40 [-1, 128, 4, 4] 147,456
BatchNorm2d-41 [-1, 128, 4, 4] 256
ReLU-42 [-1, 128, 4, 4] 0
Conv2d-43 [-1, 512, 4, 4] 65,536
BatchNorm2d-44 [-1, 512, 4, 4] 1,024
Conv2d-45 [-1, 512, 4, 4] 131,072
BatchNorm2d-46 [-1, 512, 4, 4] 1,024
ReLU-47 [-1, 512, 4, 4] 0
Bottleneck-48 [-1, 512, 4, 4] 0
Conv2d-49 [-1, 128, 4, 4] 65,536
BatchNorm2d-50 [-1, 128, 4, 4] 256
ReLU-51 [-1, 128, 4, 4] 0
Conv2d-52 [-1, 128, 4, 4] 147,456
BatchNorm2d-53 [-1, 128, 4, 4] 256
ReLU-54 [-1, 128, 4, 4] 0
Conv2d-55 [-1, 512, 4, 4] 65,536
BatchNorm2d-56 [-1, 512, 4, 4] 1,024
ReLU-57 [-1, 512, 4, 4] 0
Bottleneck-58 [-1, 512, 4, 4] 0
Conv2d-59 [-1, 128, 4, 4] 65,536
BatchNorm2d-60 [-1, 128, 4, 4] 256
ReLU-61 [-1, 128, 4, 4] 0
Conv2d-62 [-1, 128, 4, 4] 147,456
BatchNorm2d-63 [-1, 128, 4, 4] 256
ReLU-64 [-1, 128, 4, 4] 0
Conv2d-65 [-1, 512, 4, 4] 65,536
BatchNorm2d-66 [-1, 512, 4, 4] 1,024
ReLU-67 [-1, 512, 4, 4] 0
Bottleneck-68 [-1, 512, 4, 4] 0
Conv2d-69 [-1, 128, 4, 4] 65,536
BatchNorm2d-70 [-1, 128, 4, 4] 256
ReLU-71 [-1, 128, 4, 4] 0
Conv2d-72 [-1, 128, 4, 4] 147,456
BatchNorm2d-73 [-1, 128, 4, 4] 256
ReLU-74 [-1, 128, 4, 4] 0
Conv2d-75 [-1, 512, 4, 4] 65,536
BatchNorm2d-76 [-1, 512, 4, 4] 1,024
ReLU-77 [-1, 512, 4, 4] 0
Bottleneck-78 [-1, 512, 4, 4] 0
Conv2d-79 [-1, 256, 4, 4] 131,072
BatchNorm2d-80 [-1, 256, 4, 4] 512
ReLU-81 [-1, 256, 4, 4] 0
Conv2d-82 [-1, 256, 2, 2] 589,824
BatchNorm2d-83 [-1, 256, 2, 2] 512
ReLU-84 [-1, 256, 2, 2] 0
Conv2d-85 [-1, 1024, 2, 2] 262,144
BatchNorm2d-86 [-1, 1024, 2, 2] 2,048
Conv2d-87 [-1, 1024, 2, 2] 524,288
BatchNorm2d-88 [-1, 1024, 2, 2] 2,048
ReLU-89 [-1, 1024, 2, 2] 0
Bottleneck-90 [-1, 1024, 2, 2] 0
Conv2d-91 [-1, 256, 2, 2] 262,144
BatchNorm2d-92 [-1, 256, 2, 2] 512
ReLU-93 [-1, 256, 2, 2] 0
Conv2d-94 [-1, 256, 2, 2] 589,824
BatchNorm2d-95 [-1, 256, 2, 2] 512
ReLU-96 [-1, 256, 2, 2] 0
Conv2d-97 [-1, 1024, 2, 2] 262,144
BatchNorm2d-98 [-1, 1024, 2, 2] 2,048
ReLU-99 [-1, 1024, 2, 2] 0
Bottleneck-100 [-1, 1024, 2, 2] 0
Conv2d-101 [-1, 256, 2, 2] 262,144
BatchNorm2d-102 [-1, 256, 2, 2] 512
ReLU-103 [-1, 256, 2, 2] 0
Conv2d-104 [-1, 256, 2, 2] 589,824
BatchNorm2d-105 [-1, 256, 2, 2] 512
ReLU-106 [-1, 256, 2, 2] 0
Conv2d-107 [-1, 1024, 2, 2] 262,144
BatchNorm2d-108 [-1, 1024, 2, 2] 2,048
ReLU-109 [-1, 1024, 2, 2] 0
Bottleneck-110 [-1, 1024, 2, 2] 0
Conv2d-111 [-1, 256, 2, 2] 262,144
BatchNorm2d-112 [-1, 256, 2, 2] 512
ReLU-113 [-1, 256, 2, 2] 0
Conv2d-114 [-1, 256, 2, 2] 589,824
BatchNorm2d-115 [-1, 256, 2, 2] 512
ReLU-116 [-1, 256, 2, 2] 0
Conv2d-117 [-1, 1024, 2, 2] 262,144
BatchNorm2d-118 [-1, 1024, 2, 2] 2,048
ReLU-119 [-1, 1024, 2, 2] 0
Bottleneck-120 [-1, 1024, 2, 2] 0
Conv2d-121 [-1, 256, 2, 2] 262,144
BatchNorm2d-122 [-1, 256, 2, 2] 512
ReLU-123 [-1, 256, 2, 2] 0
Conv2d-124 [-1, 256, 2, 2] 589,824
BatchNorm2d-125 [-1, 256, 2, 2] 512
ReLU-126 [-1, 256, 2, 2] 0
Conv2d-127 [-1, 1024, 2, 2] 262,144
BatchNorm2d-128 [-1, 1024, 2, 2] 2,048
ReLU-129 [-1, 1024, 2, 2] 0
Bottleneck-130 [-1, 1024, 2, 2] 0
Conv2d-131 [-1, 256, 2, 2] 262,144
BatchNorm2d-132 [-1, 256, 2, 2] 512
ReLU-133 [-1, 256, 2, 2] 0
Conv2d-134 [-1, 256, 2, 2] 589,824
BatchNorm2d-135 [-1, 256, 2, 2] 512
ReLU-136 [-1, 256, 2, 2] 0
Conv2d-137 [-1, 1024, 2, 2] 262,144
BatchNorm2d-138 [-1, 1024, 2, 2] 2,048
ReLU-139 [-1, 1024, 2, 2] 0
Bottleneck-140 [-1, 1024, 2, 2] 0
Conv2d-141 [-1, 512, 2, 2] 524,288
BatchNorm2d-142 [-1, 512, 2, 2] 1,024
ReLU-143 [-1, 512, 2, 2] 0
Conv2d-144 [-1, 512, 1, 1] 2,359,296
BatchNorm2d-145 [-1, 512, 1, 1] 1,024
ReLU-146 [-1, 512, 1, 1] 0
Conv2d-147 [-1, 2048, 1, 1] 1,048,576
BatchNorm2d-148 [-1, 2048, 1, 1] 4,096
Conv2d-149 [-1, 2048, 1, 1] 2,097,152
BatchNorm2d-150 [-1, 2048, 1, 1] 4,096
ReLU-151 [-1, 2048, 1, 1] 0
Bottleneck-152 [-1, 2048, 1, 1] 0
Conv2d-153 [-1, 512, 1, 1] 1,048,576
BatchNorm2d-154 [-1, 512, 1, 1] 1,024
ReLU-155 [-1, 512, 1, 1] 0
Conv2d-156 [-1, 512, 1, 1] 2,359,296
BatchNorm2d-157 [-1, 512, 1, 1] 1,024
ReLU-158 [-1, 512, 1, 1] 0
Conv2d-159 [-1, 2048, 1, 1] 1,048,576
BatchNorm2d-160 [-1, 2048, 1, 1] 4,096
ReLU-161 [-1, 2048, 1, 1] 0
Bottleneck-162 [-1, 2048, 1, 1] 0
Conv2d-163 [-1, 512, 1, 1] 1,048,576
BatchNorm2d-164 [-1, 512, 1, 1] 1,024
ReLU-165 [-1, 512, 1, 1] 0
Conv2d-166 [-1, 512, 1, 1] 2,359,296
BatchNorm2d-167 [-1, 512, 1, 1] 1,024
ReLU-168 [-1, 512, 1, 1] 0
Conv2d-169 [-1, 2048, 1, 1] 1,048,576
BatchNorm2d-170 [-1, 2048, 1, 1] 4,096
ReLU-171 [-1, 2048, 1, 1] 0
Bottleneck-172 [-1, 2048, 1, 1] 0
AdaptiveAvgPool2d-173 [-1, 2048, 1, 1] 0
Linear-174 [-1, 10] 20,490
================================================================
Total params: 23,528,522
Trainable params: 20,490
Non-trainable params: 23,508,032
----------------------------------------------------------------
Input size (MB): 0.01
Forward/backward pass size (MB): 5.86
Params size (MB): 89.75
Estimated Total Size (MB): 95.63
----------------------------------------------------------------
[ ]
最後の方は、縦と横の次元数が1次元になってしまっていて、ニューラルネットとしてこれで意味があるのは多少不安になります。
この点については、2.3 モデルの選定で調べてみたので、その結果を参照して下さい。
1.5 学習のメインループ
やっていることは、PyTorch 学習メモ (Karasと同じモデルを作ってみた)の時と同じなのですが、学習中の出力に関しては、Kerasっぽくなるように変えてみました。コメントも前より多めにしたので、だいぶわかりやすくなったかと思います。
for i in range(nb_epoch):
train_loss = 0
train_acc = 0
val_loss = 0
val_acc = 0
#学習
net.train()
for images, labels in train_loader:
#勾配の初期化(ループの頭でやる必要あり)
optimizer.zero_grad()
# 訓練データの準備
images = images.to(device)
labels = labels.to(device)
# 順伝搬計算
outputs = net(images)
# 誤差計算
loss = criterion(outputs, labels)
train_loss += loss.item()
# 学習
loss.backward()
optimizer.step()
#予測値算出
predicted = outputs.max(1)[1]
#正解件数算出
train_acc += (predicted == labels).sum()
# 訓練データに対する損失と精度の計算
avg_train_loss = train_loss / len(train_loader.dataset)
avg_train_acc = train_acc / len(train_loader.dataset)
#評価
net.eval()
with torch.no_grad():
for images, labels in test_loader:
# テストデータの準備
images = images.to(device)
labels = labels.to(device)
# 順伝搬計算
outputs = net(images)
# 誤差計算
loss = criterion(outputs, labels)
val_loss += loss.item()
#予測値算出
predicted = outputs.max(1)[1]
#正解件数算出
val_acc += (predicted == labels).sum()
# 検証データに対する損失と精度の計算
avg_val_loss = val_loss / len(test_loader.dataset)
avg_val_acc = val_acc / len(test_loader.dataset)
print (f'Epoch [{(i+1)}/{nb_epoch}], loss: {avg_train_loss:.5f} acc: {avg_train_acc:.5f} val_loss: {avg_val_loss:.5f}, val_acc: {avg_val_acc:.5f}')
train_loss_list.append(avg_train_loss)
train_acc_list.append(avg_train_acc)
val_loss_list.append(avg_val_loss)
val_acc_list.append(avg_val_acc)
1.6 学習曲線表示
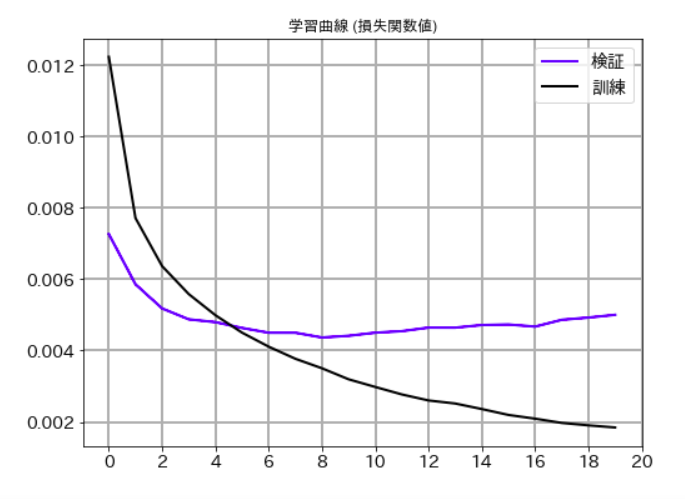
損失関数値と精度の両方について、学習曲線を表示します。コードと結果例は次のとおりです。
損失関数値
# 学習曲線 (損失関数値)
plt.figure(figsize=(8,6))
plt.plot(val_loss_list,label='検証', lw=2, c='b')
plt.plot(train_loss_list,label='訓練', lw=2, c='k')
plt.title('学習曲線 (損失関数値)')
plt.xticks(size=14)
plt.yticks(size=14)
plt.grid(lw=2)
plt.legend(fontsize=14)
plt.xticks(np.arange(0, 21, 2))
plt.show()
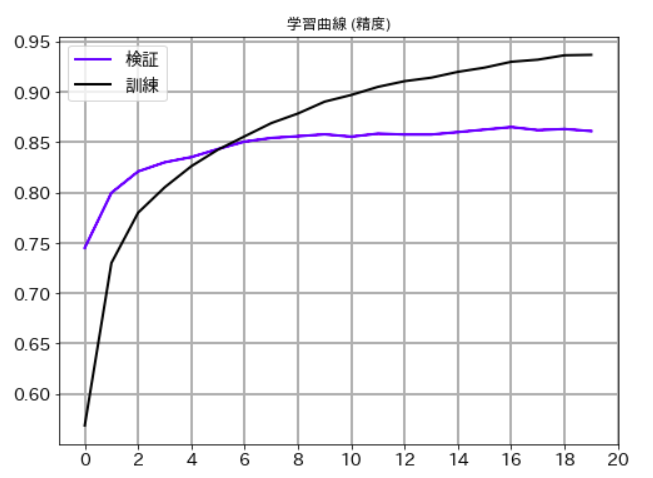
精度
# 学習曲線 (精度)
plt.figure(figsize=(8,6))
plt.plot(val_acc_list,label='検証', lw=2, c='b')
plt.plot(train_acc_list,label='訓練', lw=2, c='k')
plt.title('学習曲線 (精度)')
plt.xticks(size=14)
plt.yticks(size=14)
plt.grid(lw=2)
plt.legend(fontsize=14)
plt.xticks(np.arange(0, 21, 2))
plt.show()
2. チューニング
2.1 最適化パラメータ
詳細は省略しますが、最適化パラメータに関してはいくつかのパターンを調べた結果、下記が一番よさそうという結論になりました。
# 最適化に関しては、いくつかのパターンを調べた結果、下記が一番結果がよかった
optimizer = optim.SGD(net.parameters(),lr=0.001,momentum=0.9)
例えば、最適化関数については、Adamなども試してみましたが、SGDよりかえって学習速度が遅かったです。これは、事前学習済みモデルを使う場合に、一般的に成り立つ話のようです。
2.2 学習データの水増し
訓練データ用のtransformの定義を再掲します。
transform_train = transforms.Compose([
transforms.RandomHorizontalFlip(p=0.5), # ランダム化1
transforms.ToTensor(),
transforms.Normalize([0.5, 0.5, 0.5], [0.5, 0.5, 0.5]),
transforms.RandomErasing(p=0.5, scale=(0.02, 0.33), ratio=(0.3, 3.3), value=0, inplace=False) # ランダム化2
])
ここでは、RandomHorizontalFlipとRandomErasingという2つの呼び出しがされています。
この2つは、それぞれ「画像反転」「矩形領域の画像削除」をランダムに行う機能で、これによって、元の学習データのバリエーションを増やしています。
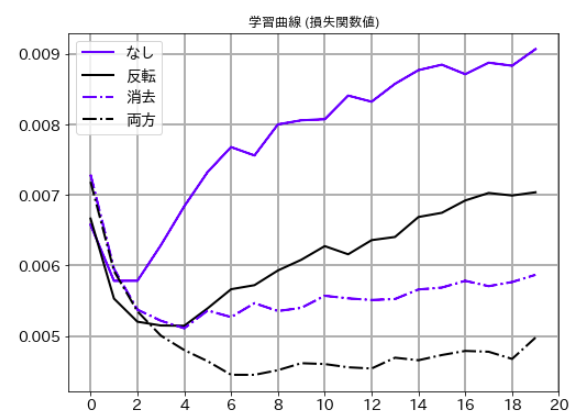
この「データ水増し」がどの程度効果があるのか確認するため、同じモデルに対して、下記の4パターンで学習をして結果を比較してみました。'下の学習曲線はいずれも検証データに対するもの)
なし: ランダム化なし
反転: 上下反転のみ
消去: 矩形消去(RandomErasing)のみ
両方: 反転と消去の両方
損失関数値
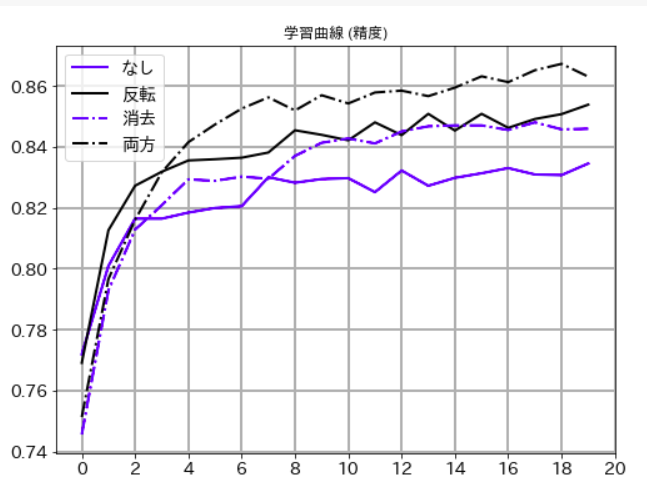
精度
グラフから明らかなように、この2つは精度向上に効果があり、しかも、独立した効果があるので組み合わせて使えることがわかります。
2.3 モデルの選定
次に読み込むモデルを取り替えて、精度がどうなるか試してみました。試したモデルは下の4つです。
Resnetに関しては、層の数が18, 50, 152の3パターンを試しました。
model_ft = models.resnet50(pretrained = True)
# model_ft = models.resnet18(pretrained = True)
# model_ft = models.resnet152(pretrained = True)
# model_ft = models.vgg19_bn(pretrained = True)
その結果(検証データに対するもの)の学習曲線のグラフを、以下に示します。
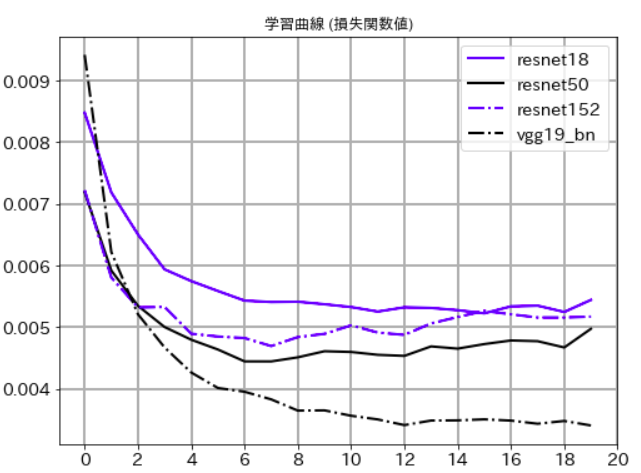
損失関数値
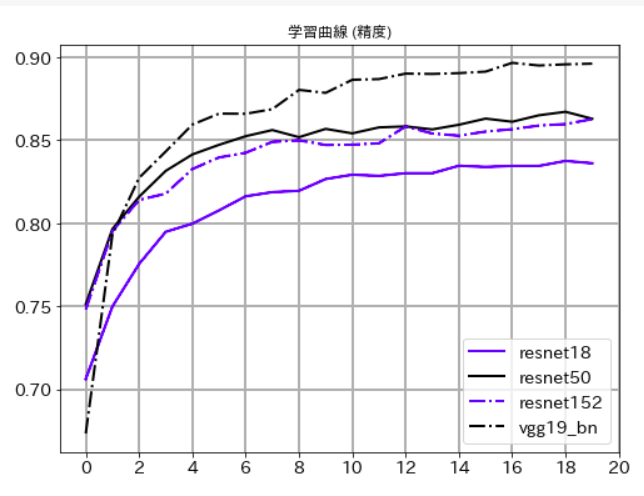
精度
まず、Resnet18とResnet50を比較するとResnet50の方がよくなっています。このことから50層程度までは、ネットワークの階層を深くすることが意味があることがわかります。
逆にResnet50とResnet152を比較した場合、ほぼ同等か、むしろResnet152の方が悪くなっている傾向があるので、CIFAR-10のように解像度が小さなデータの場合、Resnetでは50階層以上深くしても意味がないこともわかります。
最後にvgg_19_bn(bnというのはBatch Normalizationという手法を取り入れたモデルということ)ですが、圧倒的にいい結果を出しました。モデルの進化という意味ではVGGよりResNetが後に出てきたのですが、CIFAR-10のように解像度が小さなデータに対してはVGG19のような単純な構造のモデルの方が精度はいいということなのかもしれません。
3. 未解決の問題
実は、まだわからない点が一つあります。この例題自体、最初は「転移学習」のサンプルのつもりだったのです。
転移学習にするためには、モデル読み込みのところで下記のコードにすればいいはずです。
# Resnet50を重み付きで読み込む
model_ft = models.resnet50(pretrained = True)
# 最終段以外の勾配計算をしない
for param in model_ft.parameters():
param.requires_grad = False
# 最終段だけ付け替える(分類先クラス数=10)
model_ft.fc = nn.Linear(model_ft.fc.in_features, 10)
# GPUの割り当て
net = model_ft.to(device)
# 損失関数は交差エントロピー関数
criterion = nn.CrossEntropyLoss()
# 最適化計算も最終段のみ行う
optimizer = optim.SGD(net.fc.parameters(), lr=0.001, momentum=0.9)
しかし。。。
何度試してみても下記のような結果になり、全然いい精度が出ないのです。
この理由について、わかる方がいらっしゃったら、教えていただけると幸いです。
Epoch [1/20], loss: 0.01858 acc: 0.35722 val_loss: 0.01631, val_acc: 0.45390
Epoch [2/20], loss: 0.01665 acc: 0.43014 val_loss: 0.01546, val_acc: 0.47900
Epoch [3/20], loss: 0.01618 acc: 0.44372 val_loss: 0.01509, val_acc: 0.49140
Epoch [4/20], loss: 0.01587 acc: 0.45340 val_loss: 0.01479, val_acc: 0.49960
Epoch [5/20], loss: 0.01562 acc: 0.45984 val_loss: 0.01468, val_acc: 0.50190
Epoch [6/20], loss: 0.01548 acc: 0.46750 val_loss: 0.01429, val_acc: 0.51690
Epoch [7/20], loss: 0.01537 acc: 0.47066 val_loss: 0.01421, val_acc: 0.51670
Epoch [8/20], loss: 0.01524 acc: 0.47468 val_loss: 0.01412, val_acc: 0.51730
Epoch [9/20], loss: 0.01511 acc: 0.47828 val_loss: 0.01418, val_acc: 0.51480
Epoch [10/20], loss: 0.01504 acc: 0.47974 val_loss: 0.01401, val_acc: 0.52380
Epoch [11/20], loss: 0.01497 acc: 0.48228 val_loss: 0.01390, val_acc: 0.52660
Epoch [12/20], loss: 0.01491 acc: 0.48466 val_loss: 0.01389, val_acc: 0.53050
Epoch [13/20], loss: 0.01485 acc: 0.48774 val_loss: 0.01375, val_acc: 0.53290
Epoch [14/20], loss: 0.01481 acc: 0.48686 val_loss: 0.01379, val_acc: 0.52630
Epoch [15/20], loss: 0.01476 acc: 0.48818 val_loss: 0.01380, val_acc: 0.53200
Epoch [16/20], loss: 0.01476 acc: 0.48818 val_loss: 0.01361, val_acc: 0.54190
Epoch [17/20], loss: 0.01476 acc: 0.48762 val_loss: 0.01362, val_acc: 0.53570
Epoch [18/20], loss: 0.01464 acc: 0.49438 val_loss: 0.01352, val_acc: 0.53940
Epoch [19/20], loss: 0.01462 acc: 0.49442 val_loss: 0.01349, val_acc: 0.54160
Epoch [20/20], loss: 0.01464 acc: 0.49370 val_loss: 0.01355, val_acc: 0.53710
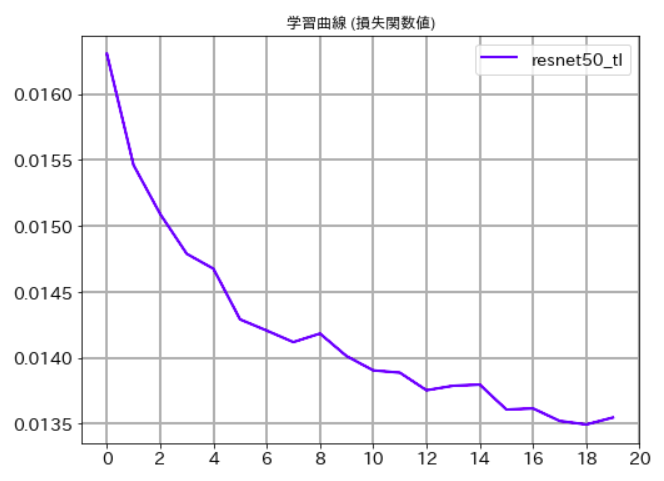
学習曲線(損失関数)
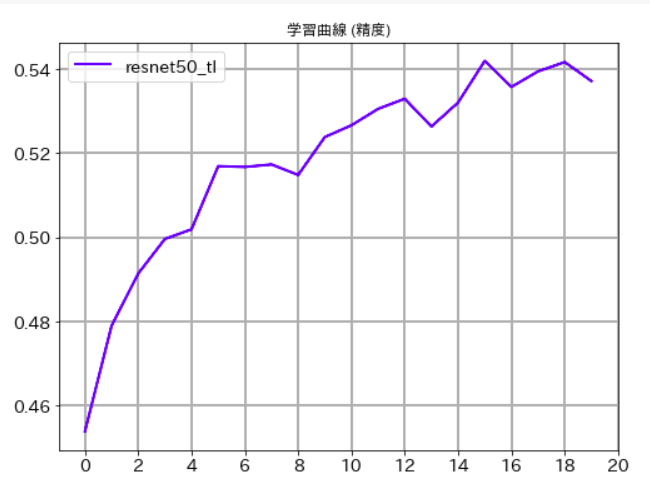
学習曲線(精度)
2021-10-10 追記
ここで説明したノウハウを含めてPyTorchの書籍を出版しました。
紹介記事をqiitaに掲載しましたので、こちらもあわせてご参照いただけると幸いです。