はじめに
まだ、あまり知られていないのですが、クラウドのWatson Studioでは、CPLEXと呼ばれる、最適化問題を解くツールがPythonから使えるようになっています。
(クラウド上のサービスの正式名称がDecision Optimaizationです。)
その機能の紹介をします。
題材としては、日本人ならみんな知っていると思われるパズル「数独」を取りあげます。
[2020-03-16 githubのリポジトリ移動]
[2020-04-25 セットアップ手順変更]
Decision Optimizationの動作原理
もともとあった製品としてのCPLEXでは、Eclipse上の開発ツール(IBM ILOG CPLEX Optimization Studio(COS)を使って、Optimization Programming Language(OPL)という言語によるモデル定義を生成します。
クラウド上のDecision Optimizationは、これと同等のモデルをPythonのAPIによって呼び出すスタイルになります。クラウド上でOPLによるモデルを取り込んで使える機能は近々サポートされる予定です。
今回は、Python APIでCLPEXを呼び出すやりかたを取ることにします。
APIの利用方法
クラウドのWatson Studio上で、このPython APIを呼び出すのはとても簡単です。
Notebook作成時のEnvironment設定で、「Python 3.6x+DO」となっているものを選ぶだけです。そう、DOとはDecision Optimizationの略だったのですね。(私もつい最近知りました)
サンプルコード
Jupyter Notebookで動くサンプルコードは
https://github.com/IBMDecisionOptimization/docplex-examples
に公開されています。
今回はここに入っていたsudokuを、コメントを日本語化して、コードを一部わかりやすくしたものを私のgithubにアップしておきました。
コード全体は、
https://github.com/makaishi2/sample-notebooks/blob/master/cplex/sudoku-aka.ipynb
にあります。
試してみよう
論より証拠、とにかく試してみましょう。
まだ、IBM Cloudのアカウントを持っていない方は、この機会に大至急アカウントを取得して下さい。
クレジットカードなしに、無期限で利用可能なLiteアカウントがあります。
手順は、
無料でなんでも試せる! Watson Studioセットアップガイド
を参照して下さい。
ここに書かれた手順の登録が一通り終わったら、次のリンクから今作ったWatson Studioのプロジェクトを選択します。
プロジェクト管理の画面になったら、画面上部の「Add to project」をクリックします。
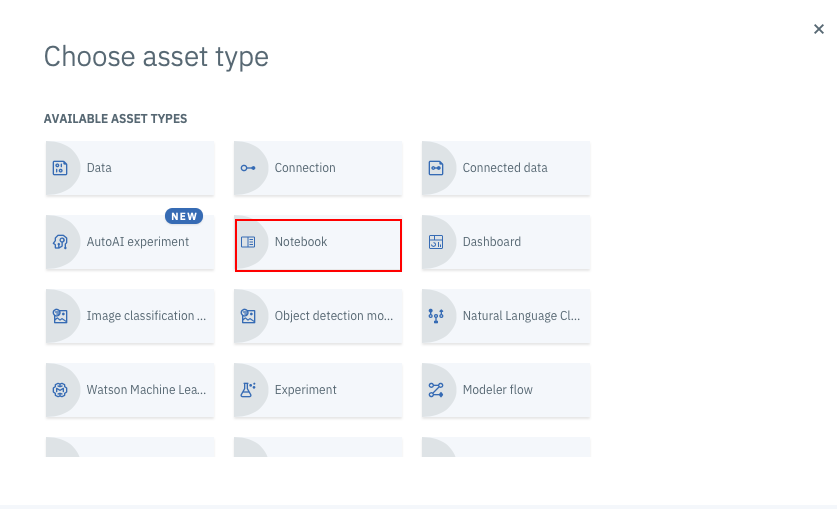
下の画面になったらNotebookを選択します。
次のNotebook作成画面になったら次の操作をします。
①「From URL」タブをクリック
② Nameの入力。なんでもいいですが、仮にSUDOKUとしています。
③ Select runtime を「Default Python 3.6XS + DO」に変更します(重要)
④ Notebook URLの欄に下記URLを入力
⑤ 画面右下の「Create Notebook」ボタンをクリック
下の画面になったら、shift + enterでセルを上から順に実行していきます。
ちなみに、SUDOKU_PROPLEM_X が問題の定義です。ここを差し替えれば、あなた自身の数独を解かせることもできます。
うまくいくと、最後にこんな結果が表示されるはずです。
コード解説
問題データの定義
この部分は、通常のPythonのコードなので、説明は省略します。
# GRNG: Grid Range
GRNG = range(9)
SUDOKU_PROBLEM_X = ( (0, 0, 0, 0, 1, 5, 0, 7, 0),
(6, 3, 0, 8, 0, 0, 0, 0, 0),
(0, 0, 8, 0, 4, 0, 0, 0, 0),
(0, 2, 5, 0, 0, 0, 0, 4, 0),
(3, 0, 0, 4, 7, 0, 2, 0, 0),
(1, 0, 0, 0, 0, 0, 0, 6, 0),
(8, 0, 0, 0, 0, 6, 0, 0, 0),
(0, 0, 0, 0, 2, 0, 0, 0, 0),
(0, 7, 2, 1, 0, 0, 0, 9, 0)
)
import numpy as np
import matplotlib.pyplot as plt
# 表示用関数
def draw_grid(values):
%matplotlib inline
fig, ax = plt.subplots(figsize =(4,4))
min_val, max_val = 0, 9
R = range(0,9)
for l in R:
for c in R:
v = values[c][l]
s = " "
if v > 0:
s = str(v)
ax.text(l+0.5,8.5-c, s, va='center', ha='center')
ax.set_xlim(min_val, max_val)
ax.set_ylim(min_val, max_val)
ax.set_xticks(np.arange(max_val))
ax.set_yticks(np.arange(max_val))
ax.grid()
plt.show()
# 問題の表示
draw_grid(SUDOKU_PROBLEM_X)
CPLEXによる問題定義
ここが、CPLEX呼出しの本質的な部分です。
行単位で、コメントをいれておきましたので、それを読むとだいたいの様子はわかるかと思います。
# ライブラリインポート
from docplex.cp.model import *
# モデルの生成
mdl = CpoModel(name="Sudoku")
# 決定変数の定義
# 9 x 9 の配列に Clc という名前のCPLEX変数を定義します (C00, C01,.. C88)
# それぞれの変数は1から9までの整数値を取ります
grid = [[integer_var(min=1, max=9, name="C" + str(l) + str(c)) for l in GRNG] for c in GRNG]
# 制約の定義
# 制約条件を定義していきます
# 同一行に同じ整数値をもってはいけない
# all_diff は「すべての要素が同じではいけない」という意味の制約を表現する関数です
for l in GRNG:
mdl.add(all_diff([grid[l][c] for c in GRNG]))
# 同一列に同じ整数値をもってはいけない
for c in GRNG:
mdl.add(all_diff([grid[l][c] for l in GRNG]))
# 3 x 3 の矩形領域に同じ整数値があってはいけない
ssrng = range(0, 9, 3)
for sl in ssrng:
for sc in ssrng:
mdl.add(all_diff([grid[l][c] for l in range(sl, sl + 3) for c in range(sc, sc + 3)]))
# 初期条件の設定
# C00からC88までのCPLEX変数に初期条件をとて与えられている値を設定していきます
# 設定は set_domainという関数で行います。
# 例えばマス目の値が7の場合該当する変数に対して
# Cxx.set_domain(7, 7) (7以上7以下の値を設定) という設定を行います。
for l in GRNG:
for c in GRNG:
v = problem[l][c]
if v > 0:
grid[l][c].set_domain((v, v))
# 設定した変数名と値の表示
print(grid[l][c])
最後のprint文の結果は次のようになります。
C40 = intVar(1, 1)
C50 = intVar(5, 5)
C70 = intVar(7, 7)
C01 = intVar(6, 6)
C11 = intVar(3, 3)
C31 = intVar(8, 8)
C22 = intVar(8, 8)
C42 = intVar(4, 4)
C13 = intVar(2, 2)
C23 = intVar(5, 5)
C73 = intVar(4, 4)
C04 = intVar(3, 3)
C34 = intVar(4, 4)
C44 = intVar(7, 7)
C64 = intVar(2, 2)
C05 = intVar(1, 1)
C75 = intVar(6, 6)
C06 = intVar(8, 8)
C56 = intVar(6, 6)
C47 = intVar(2, 2)
C18 = intVar(7, 7)
C28 = intVar(2, 2)
C38 = intVar(1, 1)
C78 = intVar(9, 9)
CPLEXによる解の取得
これで準備は整いました。後はモデルのslove関数を呼び出すと数独の問題を解いてくれます。
print('Solving model....')
msol = mdl.solve(TimeLimit=10)
print('Solved!')
さすがCPLEXです。「難問」を選んだつもりだったのですが、あっという間に答えを出してくれました。
結果の確認
最後に結果を確認してみます。
draw_grid(problem)
sol = [[msol[grid[l][c]] for c in GRNG] for l in GRNG]
print('Solve time: ', msol.get_solve_time())
draw_grid(sol)
こんな結果がでてくれば成功です。
おまけ
上で紹介した数独より実業務に近い問題である「oil blending」もコメント日本語化をしてみました。使い方は上の例と同じです。
ソースをブラウザで見る場合のURL
https://github.com/makaishi2/sample-data/blob/master/notebooks/oil-blendung.ipynb
Watson StudioのJupyterにロードする場合のURL
https://raw.githubusercontent.com/makaishi2/sample-data/master/notebooks/oil-blendung.ipynb