はじめに
Watsonで数独を解く! Decision Optimizerを使ってみたに引き続きDecision Optimizerシリーズ第二段です。
今回はあまりにも有名な問題「巡回セールスマン問題」にチャレンジしてみます。
[2020-03-16 githubのリポジトリ移動]
巡回セールスマン問題とは
一人のセールスマンが、N箇所の場所を一筆書きで回りたい。この場合に最短時間で回れるコースをどうやってみつけるか?
という問題です。
数学的には「NP困難」と呼ばれる領域の問題で、少しNが大きくなると、調べるべき組み合わせの数が爆発的に増大し、完全解を求められないことがわかっています。より詳しい話は、下記のWikipediaの記事を参照してください。
CPLEXの2つのライブラリ
これから、この問題をCPLEXを使って解いていくのですが、その前にCPLEXの2種類のライブラリについて説明しておきます。
Mathematical Programming Modeling (MP) と呼ばれるライブラリと、Constraint Programming Modeling (CP) と呼ばれるライブラリがその2つです。
前回紹介した「数独」は、CPで解く種類の問題です。
前回の記事の最後に紹介した「原油のブレンド問題」は、MPで解く問題となります。違いは、MPの場合は目的関数と呼ばれる関数があり、この関数の値を最大にする組み合わせをみつける問題である点となります。今回解く、巡回セールスマン問題も、移動距離合計という目的関数が存在するのでMPで解くべき問題ということになります。
(注)一点補足すると、上で説明した「NP困難」の数学的事実はCPLEXでも解決することはできません。
CPLEXは「NP困難な問題に対しても実用上問題のない次善の解(最適解ではない)を、実用になる有限時間で見つけるツール」と理解してもらえればいいです。
もう一点補足すると、最近注目を浴びている「量子コンピュータ」は、まったく新しい技術要素を用いて、この問題に対する最適解を有限時間で求めようとしているアプローチということになります。
数学的原理
CPLEXで問題を解く場合、制約や目的関数など、数学的な原理を事前に明確にしておく必要があります。
前回紹介した数独では、この原理はほぼ自明なものだったのですが、今回は結構数式としての記述が難しい問題になります。
この点に関しては、下記リンク先の情報を参考にさせてもらいました。
ただ、条件式に関しては、コードで表現しやすいように、一部同値な式で書き直しています。
($x_{ii} = 0$という制約を付け加えることで、条件式を簡略化した)
最終的な数式を書き直すと、次のようになります。
この式の中で$x_{ij}とu_{i}$がどういう意味を持つかについては、下のPythonコードのコメントのところに書いておきましたので、そちらを参照して下さい。
なんとなく$u_iはいらなくてx_{ij}$だけでいいのではという気がするのですが、この変数は、2個以上の小さなループの集合になる解を排除して、全体で一つの大きなループにするために必要な変数です。このことを記述しているのが、制約式の一番最後にある謎の式で、どうしてこれでいいかについては、上のリンク先記事を参照して下さい。
$ x_{ii} = 0 $ $(i = 0, 1, .. N-1)$
$ 0 \leqq x_{ij} \leqq 1$ $i\ne j$ $(i, j = 0, 1, .., N-1)$
$\displaystyle\sum_{i=0}^{N-1} x_{ij} = 1$ $(j = 0, 1, .. N-1)$
$\displaystyle\sum_{j=0}^{N-1} x_{ij} = 1$ $(i = 0, 1, .. N-1)$
$ u_0 = 0$
$ 1 \leqq u_i \leqq N-1$ $(i = 1, 2, .., N-1)$
$u_i - u_j + N \cdot x_{ij} \leqq N-1$ $(i, j = 0, 1, .., N-1)$
また、目的関数は次の式になります。
$ cost = \displaystyle\sum_{i=0}^{N-1}\displaystyle\sum_{j=0}^{N-1}
c_{ij}x_{ij}
$
Jupyter Notebookコード
ここまでの準備ができれば、後は上の数式をPython APIで表現するだけです。
実装コードの全体は、
https://github.com/makaishi2/sample-notebooks/blob/master/cplex/TSP.ipynb
にアップしてあります。
また、前の記事のようにURL指定でWatson StudioのJupyter Notebookにロードする場合は、次のURLを指定して下さい。
結果概要
オリジナルデータは48件分あります。
Notebookのコードでは、変数Nの設定で、このうち何件分のデータで最適化を行うか、指定できるようになっています。
かかった時間は25件の場合で約10秒、30件の場合で約4分弱でした。
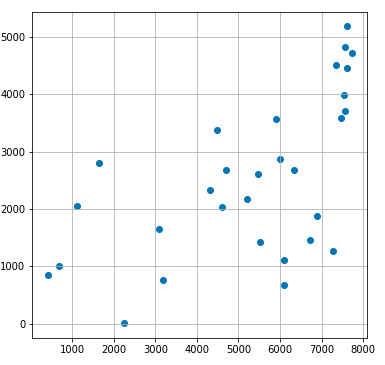
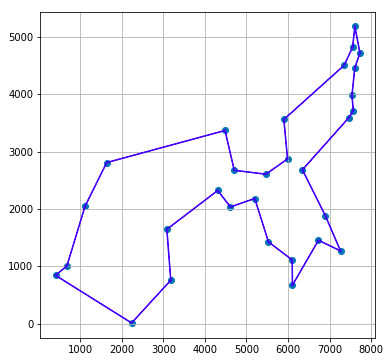
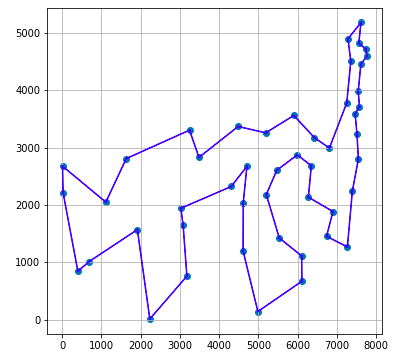
30件の場合の元データ散布図と、それに対してCPLEXが示した解によるルート図を以下に示します。
コード解説
いつものようにコードの簡単な解説を以下に示します。
問題データのロード
ライブラリロード
# ライブラリのロード
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from IPython.display import display
データのロード
オリジナル問題の48件分のデータを、githubからロードする作りにしました。
# データのロード
# 48件は巡回セールスマン問題のオリジナルデータです
url = 'https://raw.githubusercontent.com/makaishi2/sample-data/master/data/att48.csv'
df = pd.read_csv(url)
display(df.head())
print('size = ', df.values.shape)
下の図のような結果が返ってくるはずです。
対象項目絞り込み
Nの変数設定で、分析対象項目の絞り込みを行います。絞り込んだ結果に関しては散布図表示しています。
# 対象項目数
# N = 25 は10秒程度で解決
# N = 25
# N=30 は4分弱かかる
N = 30
# これ以上の値での結果は未確認
# 絞り込んだデータを使って、初期化と散布図表示
data = df[:N]
data_np = np.array(data)
plt.figure(figsize=(6,6))
plt.scatter(data_np[:,0], data_np[:,1])
plt.grid()
plt.show()
コスト配列の作成
任意のノード間のコストの配列(c)を座標値から計算します。
下の例では便宜上ユークリッド距離にしていますが、この距離の値をGoogle APIなど利用して2点間の実距離に差し替えれば、そのままリアルな最適化問題として使えるかと思います。
# 距離関数の定義
# 便宜上ユークリッド距離にしています
def distance(i, j):
return np.sqrt(np.sum((data_np[i,:] - data_np[j,:])** 2))
# コスト配列の定義
c = np.zeros((N,N))
for i in range(N):
for j in range(N):
c[i, j] = distance(i, j)
CPLEX APIによる問題定義
ここから先は、CPLEX APIを利用した、問題定義となります。
環境の確認
最初に次のAPI呼出しで、環境を確認してみます。
# CPLEX環境の確認
from docplex.mp.environment import Environment
env = Environment()
env.print_information()
手元の環境では、次のような結果になりました。
* system is: Linux 64bit
* Python version 3.6.8, located at: /opt/conda/envs/Python36/bin/python
* docplex is present, version is (2, 10, 150)
* CPLEX library is present, version is 12.9.0.1, located at: /opt/conda/envs/Python36/lib/python3.6/site-packages
* pandas is present, version is 0.24.1
モデルの定義
最初にモデルインスタンスの定義を行います。TSPは「Traveling Salesman Problem」の略です。
# モデルの宣言
from docplex.mp.model import Model
mdl = Model(name="TSP")
モデルパラメータの設定
モデルに対しては必要に応じてパラメータ設定ができるようです。下記のサンプルではスレッド数(MAXは2のようです)と最大時間数を設定しています。
(他にどんなことができるかは現在調査中)
# モデルのパラメータ定義
# スレッド数: 2
mdl.parameters.threads = 2
# 最大時間数: 600秒
mdl.parameters.timelimit = 600
決定変数の宣言
次は決定変数の宣言です。
決定変数が行列型のxと配列型のuの二種類を宣言します。それぞれの意味・目的はコメントに記載しておきました。
# 決定変数の宣言
# x : 移動matrix
# i番目のノードからj番目のノードに移動する時 x_ij = 1
# それ以外の場合 x_ij = 0
x = mdl.integer_var_matrix(N, N)
# u: 順序変数
# 0番目のノードの次に移動するノードがiの場合
# u[i] = 1
# その次に移動するノードがjの場合
# u[j] = 2
# .. のように定義する
u = mdl.integer_var_list(N)
制約の定義
次に制約の定義を行います。
元になる数式は、前の節に記載しておきましたので、そちらを参照して下さい。
# u(順序変数)の制約
# 最初のノードは0番目 : u[0] = 0
# それ以外の順序変数は1以上 N-1以下
mdl.add_constraint(u[0] == 0)
for i in range(1, N):
mdl.add_constraint(u[i] >= 1)
mdl.add_constraint(u[i] <= N-1)
# x(移動matrix)の制約
# 自分から自分への移動はないので、u_ii = 0
# それ以外の場合は u_ij は0か1
for i in range(N):
for j in range(N):
if i == j:
mdl.add_constraint(x[i, j] == 0)
else:
mdl.add_constraint(x[i, j] >= 0)
mdl.add_constraint(x[i, j] <= 1)
# x(移動matirx)に関する縦の制約
for i in range(N):
mdl.add_constraint(mdl.sum(x[i, j] for j in range(N)) == 1)
# x(移動matirx)に関する横の制約
for j in range(N):
mdl.add_constraint(mdl.sum(x[i, j] for i in range(N)) == 1)
# 部分路制約
# ループが全体で1つであるための条件
# 参考リンク http://satemochi.blog.fc2.com/blog-entry-24.html
for i in range(1, N):
for j in range(1, N):
mdl.add_constraint(u[i] - u[j] + N * x[i,j] <= N -1)
最適化関数の定義
最後に最適化関数の定義を行います。
# 総移動コスト
total_cost = mdl.sum(c[i, j] * x[i, j] for i in range(N) for j in range(N))
# 最適化の定義
mdl.minimize(total_cost)
設定の確認
これでモデルの記述は全部終わりました。
最後にprint_information関数で、記述のサマリーを確認します。
# 制約設定の確認
mdl.print_information()
下記のような結果が返ってくるはずです。
Model: TSP
- number of variables: 930
- binary=0, integer=930, continuous=0
- number of constraints: 2730
- linear=2730
- parameters: defaults
- problem type is: MILP
元のノード数が30個の場合で、決定変数の数が930個、制約の数は2730個になっています。
これはとても人間の力では解けないので、ツールにお任せするしかなさそうです。
問題を解く
いよいよsolve関数を呼び出して、問題を解きます。
今回は、log_outputのオプションも付けて、途中経過の表示も行ってみましょう。
# 問題を解く
# ログ出力をONにして、詳細情報も表示します
mdl.solve(log_output = True)
mdl.report()
下記のような結果が返ってくるはずです。
WARNING: Number of workers has been reduced to 2 to comply with platform limitations.
CPXPARAM_Read_DataCheck 1
CPXPARAM_Threads 2
Tried aggregator 1 time.
MIP Presolve eliminated 1858 rows and 31 columns.
MIP Presolve modified 1624 coefficients.
Reduced MIP has 872 rows, 899 columns, and 4176 nonzeros.
Reduced MIP has 870 binaries, 29 generals, 0 SOSs, and 0 indicators.
Presolve time = 0.01 sec. (3.03 ticks)
Probing time = 0.01 sec. (2.90 ticks)
Tried aggregator 1 time.
Reduced MIP has 872 rows, 899 columns, and 4176 nonzeros.
Reduced MIP has 870 binaries, 29 generals, 0 SOSs, and 0 indicators.
Presolve time = 0.01 sec. (3.18 ticks)
Probing time = 0.01 sec. (2.89 ticks)
Clique table members: 466.
MIP emphasis: balance optimality and feasibility.
MIP search method: dynamic search.
Parallel mode: deterministic, using up to 2 threads.
Root relaxation solution time = 0.00 sec. (1.41 ticks)
Nodes Cuts/
Node Left Objective IInf Best Integer Best Bound ItCnt Gap
* 0+ 0 86255.7609 0.0000 100.00%
0 0 18184.3571 62 86255.7609 18184.3571 51 78.92%
0 0 20769.9760 72 86255.7609 Cuts: 93 94 75.92%
0 0 20848.4887 72 86255.7609 Cuts: 45 126 75.83%
0 0 20848.4887 72 86255.7609 Cuts: 43 141 75.83%
0 0 20848.4887 71 86255.7609 Cuts: 15 152 75.83%
* 0+ 0 41843.4590 20848.4887 50.18%
0 2 20848.4887 71 41843.4590 20848.4887 152 50.18%
Elapsed time = 0.18 sec. (85.35 ticks, tree = 0.02 MB, solutions = 2)
* 141 109 integral 0 32550.0557 20852.8478 1158 35.94%
* 239+ 162 32483.1076 20859.3823 35.78%
* 246 187 integral 0 32154.2342 20859.3823 1971 35.13%
(途中略)
325448 20165 cutoff 25354.1056 25157.6747 2674217 0.77%
334254 15022 cutoff 25354.1056 25192.3348 2742881 0.64%
343461 8762 cutoff 25354.1056 25244.3208 2809424 0.43%
Elapsed time = 221.50 sec. (173320.15 ticks, tree = 7.03 MB, solutions = 19)
GUB cover cuts applied: 22
Clique cuts applied: 12
Cover cuts applied: 22
Implied bound cuts applied: 15
Flow cuts applied: 1
Mixed integer rounding cuts applied: 102
Zero-half cuts applied: 41
Multi commodity flow cuts applied: 1
Lift and project cuts applied: 21
Gomory fractional cuts applied: 22
Root node processing (before b&c):
Real time = 0.19 sec. (85.04 ticks)
Parallel b&c, 2 threads:
Real time = 225.75 sec. (176705.75 ticks)
Sync time (average) = 3.91 sec.
Wait time (average) = 0.12 sec.
------------
Total (root+branch&cut) = 225.94 sec. (176790.79 ticks)
* model TSP solved with objective = 25354.106
詳細の確認
get_solve_details関数で、解の詳細を確認してみます。
# 詳細情報の表示
print(mdl.get_solve_details())
こんな結果が返ってくるはずです。
status = integer optimal, tolerance
time = 225.95 s.
problem = MILP
gap = 0.00996211%
結果のグラフ表示
最後に見つかった解を散布図上に表示してみましょう。
# 結果の取得
indexes = [u[i].solution_value for i in range(N)]
matrix = [[x[i, j].solution_value for j in range(N)] for i in range(N)]
ar = np.array(matrix)
# 結果の散布図上での表示
data_np = np.array(data)
plt.figure(figsize=(6,6))
plt.scatter(data_np[:,0], data_np[:,1])
for i in range(N):
for j in range(N):
if ar[i, j] == 1:
plt.plot(data_np[[i,j],0], data_np[[i,j],1], c='b')
plt.grid()
plt.show()
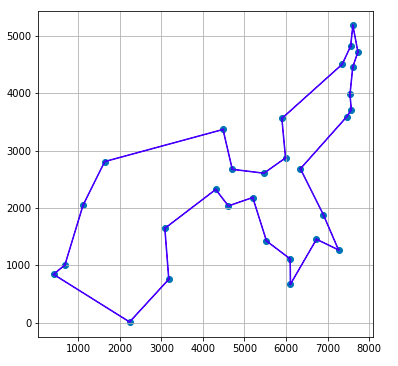
下記のようなグラフが表示されれば成功です。お疲れ様でした。
追記 Nをもっと大きな数にすると
今までの記事で、Nをもっと大きくすると、どうなるのか知りたいと思います。
私も知りたいのでやってみました。
驚いたことに、N=35とN=40の場合は、N=30よりもっと短い時間で終わりました。
(N=35だと4秒、N=40だと42秒)
N=48のときは、全然終わりそうにない感じだったので、記事で紹介した時間制限を1800秒に設定しました。
※備考 Decisin OptimizerのNotebookを利用する場合、21CUH (1時間で21ユニット)の課金を使います。
Liteアカウントで利用可能な課金額は1か月で50ユニットですので、この処理を何度かやるとそれだけで課金を使いきることになります。Liteアカウントで試される場合はこの点にご注意下さい。
設定のためのコードを抜き出すと下記のとおりです。
# モデルのパラメータ定義
# スレッド数: 2
mdl.parameters.threads = 2
# 最大時間数: 1800秒
mdl.parameters.timelimit = 1800
この場合の結果を、以下に記載します。
solve関数実行中のログ
CPXPARAM_Read_DataCheck 1
CPXPARAM_Threads 2
CPXPARAM_TimeLimit 1800
Tried aggregator 1 time.
MIP Presolve eliminated 4702 rows and 49 columns.
MIP Presolve modified 4324 coefficients.
Reduced MIP has 2258 rows, 2303 columns, and 10998 nonzeros.
Reduced MIP has 2256 binaries, 47 generals, 0 SOSs, and 0 indicators.
Presolve time = 0.01 sec. (7.30 ticks)
Probing time = 0.02 sec. (4.13 ticks)
Tried aggregator 1 time.
Reduced MIP has 2258 rows, 2303 columns, and 10998 nonzeros.
Reduced MIP has 2256 binaries, 47 generals, 0 SOSs, and 0 indicators.
Presolve time = 0.01 sec. (7.74 ticks)
Probing time = 0.01 sec. (3.58 ticks)
Clique table members: 1149.
MIP emphasis: balance optimality and feasibility.
MIP search method: dynamic search.
Parallel mode: deterministic, using up to 2 threads.
Root relaxation solution time = 0.00 sec. (3.68 ticks)
Nodes Cuts/
Node Left Objective IInf Best Integer Best Bound ItCnt Gap
0 0 26762.8312 97 26762.8312 94
0 0 31288.3138 122 Cuts: 190 175
0 0 31520.2607 121 Cuts: 84 229
0 0 31520.2607 116 Cuts: 40 266
0 0 31520.2607 114 Cuts: 32 299
0 0 31520.2607 117 Cuts: 17 313
* 0+ 0 44059.9234 31520.2607 28.46%
* 0+ 0 42371.0430 31520.2607 25.61%
0 2 31520.2607 117 42371.0430 31520.2607 313 25.61%
Elapsed time = 1.34 sec. (1352.12 ticks, tree = 0.02 MB, solutions = 2)
120 109 32236.4597 44 42371.0430 31520.2607 1982 25.61%
240 222 34976.1678 105 42371.0430 31520.2607 3650 25.61%
500 414 31536.0224 104 42371.0430 31535.0426 6334 25.57%
783 701 41326.1454 47 42371.0430 31535.0426 10594 25.57%
* 873+ 528 41411.3945 31941.8932 22.87%
* 873+ 352 41082.6911 31941.8932 22.25%
873 353 31941.8932 116 41082.6911 31941.8932 12784 22.25%
875 355 31961.3763 126 41082.6911 31962.3013 12809 22.20%
898 366 32044.5635 122 41082.6911 31963.5683 12886 22.20%
* 900+ 226 41075.0765 31963.5683 22.18%
* 908+ 147 40864.7463 31963.5683 21.78%
* 919+ 94 39048.8864 31963.5683 18.14%
922 141 32138.2066 121 39048.8864 31963.5683 12966 18.14%
940 110 32343.3044 125 39048.8864 31969.4607 13043 18.13%
1152 219 34356.5554 97 39048.8864 31969.4607 14091 18.13%
Elapsed time = 11.57 sec. (8748.51 tick
(途中略)
396345 244626 32853.2816 122 33701.2618 32765.2102 5661464 2.78%
396975 244777 33546.2942 86 33701.2618 32766.1908 5667055 2.77%
397710 245350 33283.6134 119 33701.2618 32766.6977 5683128 2.77%
398375 245730 33650.2717 115 33701.2618 32767.1283 5695264 2.77%
399332 246349 33077.0530 142 33701.2618 32767.5542 5714250 2.77%
400233 246907 33018.6804 143 33701.2618 32768.2769 5727993 2.77%
401141 247321 32789.1947 103 33701.2618 32768.7445 5742685 2.77%
402336 247850 33147.3776 102 33701.2618 32769.1675 5755769 2.77%
Elapsed time = 1782.07 sec. (1378944.05 ticks, tree = 306.56 MB, solutions = 24)
403351 248512 33376.6836 96 33701.2618 32769.7014 5777789 2.76%
404310 249171 33303.6713 101 33701.2618 32770.4043 5800246 2.76%
405129 249660 33256.2355 120 33701.2618 32771.4467 5818181 2.76%
GUB cover cuts applied: 385
Clique cuts applied: 20
Cover cuts applied: 108
Implied bound cuts applied: 19
Flow cuts applied: 3
Mixed integer rounding cuts applied: 1147
Zero-half cuts applied: 38
Lift and project cuts applied: 4
Gomory fractional cuts applied: 31
Root node processing (before b&c):
Real time = 1.34 sec. (1351.27 ticks)
Parallel b&c, 2 threads:
Real time = 1798.67 sec. (1391470.14 ticks)
Sync time (average) = 61.04 sec.
Wait time (average) = 0.11 sec.
------------
Total (root+branch&cut) = 1800.01 sec. (1392821.41 ticks)
* model TSP solved with objective = 33701.262