はじめに
書籍『Pythonでスラスラわかる ベイズ推論「超」入門』著者です。
連休でようやくまとまった時間が取れたので、前からやってみたことを試し、その記録をここに残すことにします。
それは何かと言いますと、私の書いた7冊の本(共著を含む)のAmazonレビュー結果を使ってベイズ推論をすることです。
このシナリオは、本の6章のユースケースに含めることも考えたのですが、誰でもすぐに適用できるユースケースではなさそうなので、書籍に含めることを断念したものになります。
ベイズ推論の考え方
次の表を見て下さい。
| book | score5 | score4 | score3 | score2 | score1 | 合計 |
|---|---|---|---|---|---|---|
| Pythonで儲かるAIをつくる | 126 | 60 | 48 | 7 | 10 | 251 |
これは、私の著作の一つ『Pythonで儲かるAIをつくる』に対してAmazon上で読者からいただいたレビューを、スコア別に件数カウントしたものです(2024-01-07時点)。
ここで著者としては、「レビューの平均スコア」を知りたいです。
普通に考えると、次の計算でいいのではないかと考えがちです。
$$
\dfrac{126 \times 5 + 60 \times 4 + 48 \times 3 + 7 \times 2 + 10 \times 1}{251} = 4.135..
$$
このやりかたを数学的にまわりくどく説明すると「最尤推定」という方法に該当します。
ポイントは、計算結果が1点になっていることです。
例えば、レビュー件数が全部で9件しかないときの平均スコアが4.8であり、レビュー件数が97件のときの平均スコアが4.4だったとします。見た目の値は前者の方が高そうですが、それは件数が少ないため、たまたまスコアがよかっただけで、もっとレビュー件数が増えてくると実は後者の方が平均スコアが高い可能性もあると考えられます。
本来であれば件数に依存する「不確実性」もセットで評価したいです。
ベイズ推論が活用できるのは、まさにこのようなケースに対してです。ベイズ推論の結果を先回りして示すと、以下のようになります。

| 全体レビュー件数 | 単純平均 | ベイズ平均 | hdi_3% | hdi_97% | ベイズ偏差 | |
|---|---|---|---|---|---|---|
| ベイズ推論「超」入門 | 9 | 4.778 | 4.129 | 3.55 | 4.734 | 0.328 |
| Pythonプログラミングとデータ分析 | 16 | 4.625 | 4.232 | 3.794 | 4.726 | 0.259 |
| PyTorch &深層学習プログラミング | 97 | 4.433 | 4.359 | 4.174 | 4.522 | 0.096 |
| Pythonで儲かるAIをつくる | 251 | 4.135 | 4.111 | 3.989 | 4.238 | 0.068 |
| ディープラーニングの数学 | 210 | 4.086 | 4.058 | 3.893 | 4.207 | 0.086 |
| Python自然言語処理入門 | 23 | 3.174 | 3.149 | 2.638 | 3.706 | 0.289 |
| Watson Studioで始める機械学習・深層学習 | 8 | 3.500 | 3.303 | 2.491 | 4.077 | 0.422 |
上で引用した「儲かるAI」に関しては、単純平均とほぼ同じような結果になっていますが、件数が少ない書籍に関してはhdi_3%からhdi_97%の幅(統計学の「信頼区間」とほぼ同じ概念と考えてください)が非常に広くなっていることがわかります。
「不確実性」が具体的な数値の形で示されているのです。
では、どうするとこの結果が得られるのか。
考え方の概要を簡潔に説明すると以下のようになります。
- スコア別のレビュー件数(ベイズ推論の用語で「観測値」)の背後に確率モデルが存在することを仮定
- 確率モデルと観測値から事後分布を導出
- 事後分布に基づいて「レビューの平均スコア」も確率変数として算出する
- 得られた「確率変数としてのレビュー平均スコア」を統計的に分析する
- この形で分析をすることにより最尤推定より現実に即した判断が可能
始めてこの話を聞く人は、何をいっているのか、まったくわからないと思います。しかし、この考え方がベイズ推論の根幹部分なのです。
私は、このことを説明するために、『Pythonでスラスラわかる ベイズ推論「超」入門』を書きました。なので、この話を完全に理解されたい方は、是非、この書籍をお読みいただければと思います。
サポートサイトのリンクは下記になります。
当ユースケースにおける確率モデル定義
ここから先の説明は、先ほどご紹介した書籍でベイス推論の初歩を理解した方を対象とさせていただきます。
当記事で作る確率モデルと、書籍の実装との関係を説明すると、4.6節で説明している「ベイズ推論(二項分布バージョン)」の多項分布版だという説明が一番わかりやすいです。
4.6節の「ベイズ推論(二項分布バージョン)」の確率モデル定義のコードを抽出すると、次のようになります。
# コンテキスト定義
model2 = pm.Model()
with model2:
# pm.Uniform: 一様分布
p = pm.Uniform('p', lower=0.0, upper=1.0)
# pm.Binomial: 二項分布
# p: 成功確率
# n: 試行数
X_obs = pm.Binomial('X_obs', p=p, n=5, observed=2)
ここで、2.5節(p.50)で一様分布はベータ分布で(alpha=1.0, beta=1.0)としたケースと同じだと説明していることを思い出して下さい。すると、上の実装コードは
# コンテキスト定義
model2 = pm.Model()
with model2:
# 事前分布をベータ分布に変更
p = pm.Beta('p', alpha=1.0, beta=1.0)
# pm.Binomial: 二項分布
# p: 成功確率
# n: 試行数
X_obs = pm.Binomial('X_obs', p=p, n=5, observed=2)
と書き直せることがわかります。
これで、今回のAmazonレビュー問題を確率モデルとして記述する準備が整いました。
一言でいうと「二」→「多」という変更をかけます。
具体的なPyMCのクラス名でいうと
事前分布: ベータ分布をディリクレ分布(pm.Dirichlet)に
観測値用分布: 二項分布を多項分布(pm.Multinomial)に
ということになります。
具体的なコード雛形でいうと、次の形になります。
counts = np.array([126, 60, 48, 7, 10])
n_scores = len(counts)
sum = counts.sum()
# コンテキスト定義
model3 = pm.Model()
with model3:
# 多項分布の事前分布をディリクレ分布で行う
p = pm.Dirichlet('p', a=np.ones(n_scores))
# 観測値の設定は多項分布で行う
obs = pm.Multinomial('obs', p=p, n=sum, observed=counts)
ディリクレ分布に関しては、サポートサイトに解説記事があるので、こちらも参照して下さい。今回の確率モデルを作る上でのポイントだけ説明すると、ベータ分布でα=1.0、β=1.0のケースが一様分布だった話の拡張で、ディリクレ分布でもaのパラメータ値が全要素1になっている(np.ones(n_scores))場合、一様分布の拡張版になるということを利用しています。
上のコードと見比べるとどこがどう変わったかわかるかと思います。たったこれだけの修正で、多項分布のベイス推論ができてしまうとは、素晴らしいですね。
平均スコア算出
これで確率モデル構築まではできたのですが、もう一つ解決すべき問題があります。それは冒頭で説明した下記の部分をどのように実装するかです。
『事後分布に基づいて「レビューの平均スコア」も確率変数として算出する』
この課題に対しては次の考え方で実装をします。要は確率変数(5次元ベクトル)pを使って期待値を計算すればいいということです。
p = pm.Dirichlet('p', a=np.ones(n_scores))
によって、pには5次元の確率値の値が入ります。この確率値に対して
weights = np.array([5, 4, 3, 2, 1])
ave_score = p @ weights
のような内積計算をすれば(NumPy変数同士の内積は演算子@で計算できます)、 ave_scoreが今求めたい確率変数になります。
確率モデル構築実装
以上を踏まえた全体的な確率モデル構築実装コードは以下のようになります。
今までの説明からの変更点として、countsとweightsに関しては確率モデル可視化結果に示すため、pm.ConstDataとして定義しました。
また、最終的な分析対象であるave_scoreも、分析をしやすくするため、pm.Deterministicで定義しています。
counts = np.array([126, 60, 48, 7, 10])
n_scores = len(counts)
weights = np.array([5,4,3,2,1])
sum = counts.sum()
scores = ['score5','score4','score3','score2','score1']
# スコア用インデックス定義
coords = {'score': scores}
# コンテキスト用インスタンス生成
model1 = pm.Model(coords=coords)
# 確率モデルのコンテキスト宣言
with model1:
# スコア別レビュー件数用変数
count_data = pm.ConstantData('count_data', counts)
# 平均スコア算出用配列
weight_data = pm.ConstantData('weight_data', weights)
# 多項分布の事前分布をディリクレ分布で行う
p = pm.Dirichlet('p', a=np.ones(n_scores))
# 観測値の設定は多項分布で行う
obs = pm.Multinomial('obs', p=p, n=sum, observed=count_data)
# 平均スコアの算出結果
av_score = pm.Deterministic('av_score', p@weight_data)
# 作成した確率モデルの可視化
g = pm.model_to_graphviz(model1)
display(g)
最後の display関数で表示された確率モデル可視化結果は以下のとおりです。

サンプルコード解説
ここからは、サポートサイト(Github)にアップしてあるサンプルコードの簡単な解説をします。
Notebook全体は、下記リンク先にあります。
データ読み込み
レビュー件数に関しては、2024-01-07時点のスコア別件数を手でカウントしてexcelに入れたものを、Githubから読み取っています。気が向いたら、最新化する可能性はありますが、古いままの可能性の方が高く、その点はあらかじめお断りしておきます。
# データ読み込み
fn = 'https://github.com/makaishi2/sample-data/raw/master/data/book_scores.xlsx'
df = pd.read_excel(fn, index_col=[0])
# 重みベクトル(平均スコア算出で利用)
weights = np.array([5, 4, 3, 2, 1])
変数weightsは、平均スコア算出時に用いる重みベクトルです。
データ確認
読み込んだExcelの内容を簡単に確認します。
display(df)
結果は以下のとおりになります。
| book | score5 | score4 | score3 | score2 | score1 |
|---|---|---|---|---|---|
| ベイズ推論「超」入門 | 7 | 2 | 0 | 0 | 0 |
| Pythonプログラミングとデータ分析 | 12 | 3 | 0 | 1 | 0 |
| PyTorch &深層学習プログラミング | 63 | 17 | 13 | 4 | 0 |
| Pythonで儲かるAIをつくる | 126 | 60 | 48 | 7 | 10 |
| ディープラーニングの数学 | 116 | 32 | 39 | 10 | 13 |
| Python自然言語処理入門 | 8 | 2 | 4 | 4 | 5 |
| Watson Studioで始める機械学習・深層学習 | 3 | 2 | 1 | 0 | 2 |
インデックス作成
後で必要なので、行と列のインデックスをそれぞれリストとして作っておきます。
# 列インデックス
scores = list(df.columns)
n_scores = len(scores)
print(f'列インデックス: {scores}')
print(f'列数: {n_scores}')
# 行インデックス
books = list(df.index)
print(f'行インデックス: {books}')
print関数の結果はこんな形になります。
列インデックス: ['score5', 'score4', 'score3', 'score2', 'score1']
列数: 5
行インデックス: ['ベイズ推論「超」入門', 'Pythonプログラミングとデータ分析 ', 'PyTorch &深層学習プログラミング', 'Pythonで儲かるAIをつくる', 'ディープラーニングの数学', 'Python自然言語処理入門', 'Watson Studioで始める機械学習・深層学習']
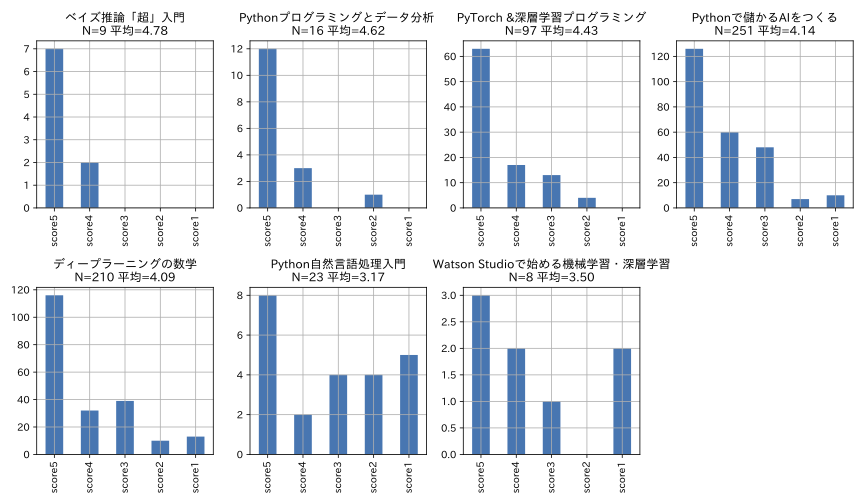
グラフ表示
この表データを棒グラフ表示してみます。
同時に、書籍ごとの全レビュー件数と、単純計算による平均スコアも算出してみました。
# グラフ描画用各種設定
plt.rcParams['figure.figsize'] = (12, 7)
fig, axes = plt.subplots(2, 4)
axes = axes.reshape(-1)
plt.rcParams["font.size"] = 10
for i, book in enumerate(books):
# 特定書名の件数抽出
counts = df.loc[book]
# 合計レビュー数
sum = counts.sum()
# 平均スコア
ave = counts@weights/sum
# 描画対象の選定
ax = axes[i]
# 棒グラフ表示
counts.plot.bar(ax=ax)
ax.set_title(f'{book}\nN={sum} 平均={ave:.02f}')
# 最後の領域は空白に設定
ax = axes[-1]; ax.set_xticks([]); ax.set_yticks([]); ax.axis('off')
# 全体レイアウトの調整
plt.tight_layout()
plt.show()
こんな結果が得られます。
確率モデル構築
ここからが、いよいよベイズ推論固有の話になります。
最終的には、ループを回して7冊の書籍すべてのベイズ推論をするのですが、ループの中身の実装確認の目的で、特定の書籍用のデータ準備から行います。具体的な書籍は、先ほどからサンプルで取り上げている「Pythonで儲かるAIをつくる」にしました。
特定のモデル用のデータ準備
book = books[3]
counts = df.loc[book]
sum = counts.sum()
print(f'書名: {book}')
print(f'スコア別レビュー件数:\n{counts}')
print(f'合計レビュー件数: {sum}')
print関数の出力は以下のようになります。
書名: Pythonで儲かるAIをつくる
スコア別レビュー件数:
score5 126
score4 60
score3 48
score2 7
score1 10
Name: Pythonで儲かるAIをつくる, dtype: int64
合計レビュー件数: 251
確率モデル定義
PyMCによる確率モデル定義は以下の形になります。
スコア用インデックス定義が、今までの解説でなかった箇所ですが、6.2節に解説があるので、そちらを参照されて下さい。
# スコア用インデックス定義
coords = {'score': scores}
# コンテキスト用インスタンス生成
model1 = pm.Model(coords=coords)
# 確率モデルのコンテキスト宣言
with model1:
# スコア別レビュー件数用変数
count_data = pm.ConstantData('count_data', counts)
# 平均スコア算出用配列
weight_data = pm.ConstantData('weight_data', weights)
# 多項分布の事前分布をディリクレ分布で行う
p = pm.Dirichlet('p', a=np.ones(n_scores))
# 観測値の設定は多項分布で行う
obs = pm.Multinomial('obs', p=p, n=sum, observed=count_data)
# 平均スコアの算出結果
av_score = pm.Deterministic('av_score', p@weight_data)
# 作成した確率モデルの可視化
g = pm.model_to_graphviz(model1)
display(g)
確率モデル可視化結果については、上の方で示しているので、ここでは省略します。
確率モデル定義・サンプリング・可視化・表形式の集計
以下のコードはちょっと長いのですが、書籍名でループを回しながら、確率モデル定義、サンプリング、結果可視化、表データの集計を一気にやっています。
個別要素の説明は、今まででほぼできているはずなので、細かいところはコードを直接読み解いていただければと思います。
# グラフ描画用各種設定
plt.rcParams['figure.figsize'] = (12, 6)
fig, axes = plt.subplots(2, 4)
axes = axes.reshape(-1)
plt.rcParams["font.size"] = 10
# 全体サマリー表の準備
all_summary = pd.DataFrame(None)
# サンプリング・評価は7書籍まとめて行う
for i, book in enumerate(books):
counts = df.loc[book]
ax = axes[i]
sum = counts.sum()
# スコア用インデックス定義
coords = {'score': scores}
# コンテキスト用インスタンス生成
model1 = pm.Model(coords=coords)
# 確率モデルのコンテキスト宣言
with model1:
# スコア別レビュー件数用変数
count_data = pm.ConstantData('count_data', counts)
# 平均スコア算出用配列
weight_data = pm.ConstantData('weight_data', weights)
# 多項分布の事前分布をディリクレ分布で定義
p = pm.Dirichlet('p', a=np.ones(n_scores))
# 観測値の設定は多項分布で行う
obs = pm.Multinomial('obs', p=p, n=sum, observed=count_data)
# 平均スコアの算出結果
av_score = pm.Deterministic('av_score', p@weight_data)
# サンプリング
idata1 = pm.sample(random_seed=42)
# サンプリング結果分析
# 可視化
az.plot_posterior(idata1, var_names=['av_score'], ax=ax)
ax.set_title(f'{book}\nN={sum}')
ax.set_xlim(2,5)
# 集計表データ作成
summary = az.summary(idata1, var_names=['av_score'])
summary.insert(0, '書名', book)
summary.insert(1, '全体レビュー件数', sum)
all_summary = pd.concat([all_summary, summary])
# 最後の領域は空白に設定
ax = axes[-1]
ax.set_xticks([]); ax.set_yticks([]); ax.axis('off')
# レイアウトの整形
plt.tight_layout()
plt.show()
こんなグラフができるはずです。

このグラフを作ることが、この長い記事の最大の目的でした。
幸いにして多くの部数の出た、真ん中の3つの書籍(比例してレビュー件数が多い)は、ベイズ推論で推測される平均スコアの幅が極めて狭い範囲になっています。
逆にそれ以外の4つの書籍は、幅が非常に大きいです。
これは、「件数が多いほど推測値の確度が高くなる」という経験則とあっている結果になります。
表データの出力
最後に、先ほどループを回しながら作っていた表データの結果も確認します。
ここでは、今回の実習の冒頭で計算した「単純な方式による平均スコア」も列として追加し、2つの値が比較できるようにしました。
all_summary = all_summary.reset_index(drop=True)
all_sum1 = all_summary.set_index('書名')
# 単純平均の計算
df_ave = df.apply(lambda x: x@weights/x.sum(), axis=1)
df_ave.name = '単純平均'
# 結合
all_sum2 = pd.concat([df_ave, all_sum1], axis=1)
# 整形
all_sum3 = all_sum2.copy()
all_sum3 = all_sum3.iloc[:,:6]
all_sum3 = all_sum3[['全体レビュー件数','単純平均','mean','hdi_3%','hdi_97%','sd']]
all_sum3.columns = [
'全体レビュー件数','単純平均','ベイズ平均','hdi_3%','hdi_97%','ベイズ偏差'
]
display(all_sum3)
こんな結果になるはずです。
| 全体レビュー件数 | 単純平均 | ベイズ平均 | hdi_3% | hdi_97% | ベイズ偏差 | |
|---|---|---|---|---|---|---|
| ベイズ推論「超」入門 | 9 | 4.778 | 4.129 | 3.55 | 4.734 | 0.328 |
| Pythonプログラミングとデータ分析 | 16 | 4.625 | 4.232 | 3.794 | 4.726 | 0.259 |
| PyTorch &深層学習プログラミング | 97 | 4.433 | 4.359 | 4.174 | 4.522 | 0.096 |
| Pythonで儲かるAIをつくる | 251 | 4.135 | 4.111 | 3.989 | 4.238 | 0.068 |
| ディープラーニングの数学 | 210 | 4.086 | 4.058 | 3.893 | 4.207 | 0.086 |
| Python自然言語処理入門 | 23 | 3.174 | 3.149 | 2.638 | 3.706 | 0.289 |
| Watson Studioで始める機械学習・深層学習 | 8 | 3.500 | 3.303 | 2.491 | 4.077 | 0.422 |
冒頭で計算した平均スコアを「単純平均」、ベイス推論で得られた事後分布の平均値を「ベイズ平均」と名付け、比較してみました。
サンプル数の多い真ん中3つの書籍では、2つの値が近いことがわかります。
これに対して直近に出版した2冊は、単純平均がベイズ平均より大きめの値になっています。
これは、ベイズ推論的には、「直近の2冊はレビュー数が少ないため、たまたまスコアがよさそうに見えるが今後レビュー数が増えると、もっと低い値になるはず」ということをいっているのだと理解しました。
結果に対する著者としての解釈
今回の試行で自分として最もやりたかったのは、今後の執筆方針に向けての過去データの解釈です。
これは、業務観点では重要なのですが、関心のない方には意味のない話なので、著者のつまらない独り言だと思って、スルーして下さい。
上の表の上から5冊を分析対象とした場合、「Pythonで儲かるAIをつくる」「ディープラーニングの数学」のスコアが意外に高くないことがわかります。これは、上に示したスコア別件数グラフでわかるとおり、スコア3以下の件数が多いことに起因しています。
なぜかということを著者なりに分析すると、この2冊は今までAIと関係ない読者にかなりの数読んでいただけたからではないかと考えています。このような読者から見ると、この2冊はまだ不十分な点が多々あり、それがこの結果に結びついているのではないかと。
実は、この2冊に関しては、今後、改訂版を出すことができないか、検討しようと思っています。その際には、低いスコアのレビューコメントに改善のヒントが隠されているはずなので、そういう目的で、レビューコメントを改めて一通り読んでみようかと思っています。
この2冊と対照的なのが「PyTorch&深層学習プログラミング」です。
この本の特徴はディープラーニング用フレームワークの解説書であるため、上のような「AIと関係ない読者」が購入する可能性は極めて低いということです。発行部数は上の2冊ほどでないが、読んだ方の評価が高いということが、分析で示した読者にちょうどあった難易度設定ができたことによるのではないかというのが自己分析の結果です。
ちょっと意外だったのが、「Pythonプログラミングとデータ分析」です。ベイス推論の結果を加味したとしても、「Pythonで儲かるAIをつくる」「ディープラーニングの数学」より高いスコアであることが示唆されています。
この本は、売れ行きという観点では不十分な結果だったのですが、本の品質はそうでもなかったという風に理解すると、企画とか売り方とかに課題があったのかもというのが反省点になります。
そして、2ヶ月前に出版したばかりの「ベイズ推論「超」入門」です。
単純平均スコアは過去の書籍でナンバーワンであり、著者としてぬか喜びしていたわけですが、ベイス推論的に「今後下がるよ」と言われているので、きっとそうなのだろうと現段階では思っています。
数ヶ月後にベイスの予言があたっているかどうか、確認するのが面白そうかと思っているところです。
以上が、分析結果のすべてとなります。
長い記事にお付き合いいただき、大変ありがとうございました。