修正
Git上にあるCSVファイルをローカルへ保存する方法が間違っていたのを修正し補足画像追加しました。
まえおき
Google ColaboratoryはJupyterNotebook環境が無料で利用できるサービスです。
JupyterNotebookはipynbというファイル形式で保存されます。Google Colaboratoryは一定時間(12時間)で環境がリセットされるため、定期的に保存が必要です。
前回はGITHUB上にあるipynbファイルを読み込んで、変数の中に保存された表形式のデータをExcelでよく使う操作を行ってみました。
今回は前回の発展形としてデータの平均値、中央値、分散、標準偏差などPythonの得意とする計算を行い、データがプロットされたグラフから簡単な分析を行います。
また今回は、前回ローカルPCにインストールしたAnacondaのJupyterNotebookも使います。まだローカルPCにAnacondaをインストールしていない場合は、インストールに挑戦してみてください。ゆくゆくはローカルマシンでJupyterNotebookを使うことが多くなると思います。
Git上のファイルを読み込む
ipynbファイル
今回も、まずはあらかじめGITHUB上に置いたipynbファイルを読み込んで取得する方法を行います。
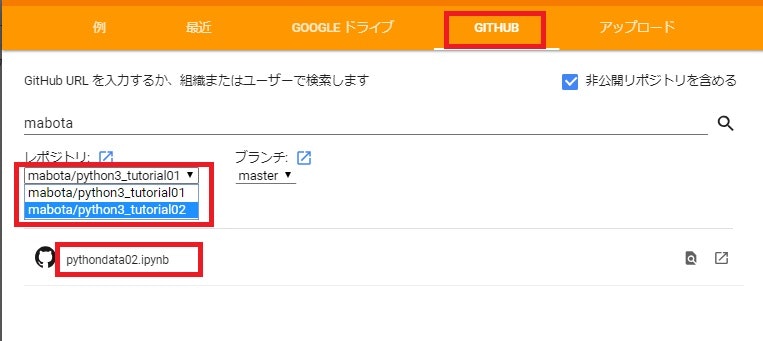
GoogleColaboratory上から、「ファイル」の「ノートブックを開く」を選択します。
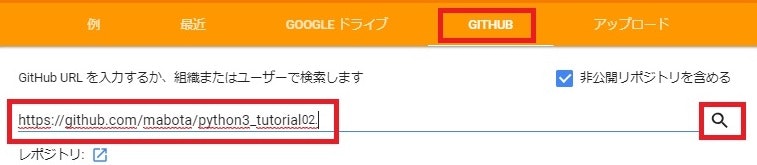
以下の画面が表示されますので、「GITHUB」のタブをクリックし、下記URLをコピーして虫眼鏡検索アイコン覧に貼り付け、虫眼鏡アイコンをクリックして検索します。
https://github.com/mabota/python3_tutorial02
検索結果に「pythondata02.ipynb」ファイルが表示されていれば、それをクリックすることで、GoogleColaboratory上で「pythondata02.ipynb」ファイルが表示されます。
※もしくは、下記画面状態の場合は「レポジトリ」から「mabota/python3_tutorial02」を選択し、表示された「pythondata02.ipynb」をクリックします。
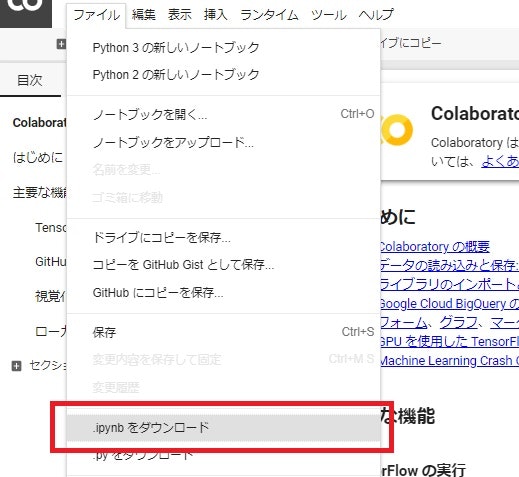
表示された新しいノートブックをローカルPCに保存するため、メニューの「ファイル」>「.ipynbをダウンロード」を選択します。
ダウンロードしたファイルはどこか自身で作業フォルダを決めて保存します。
csvファイル
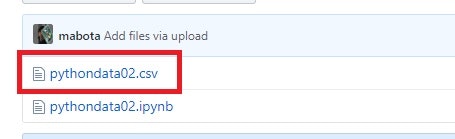
ここをクリックしてリンク先のGithubサイトにアクセスします。
画像のサイト内にある**「pythondata02.csv」**ファイルをクリックします。
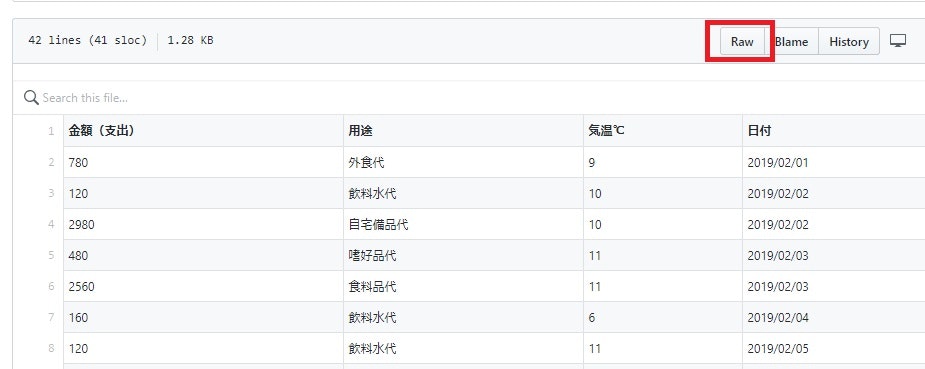
CSVファイルの内容が表示されます。このファイルをダウンロードするため、「Raw」ボタンを押します。
右クリックメニューから「名前を付けて保存」を選択し、同じくローカルPCに保存します。最初に保存した「pythondata02.ipynb」と、この「pythondata02.csv」は同じフォルダ内に置いて使います。
データの確認
ローカルPCのJupyterNotebookを起動し、最初にGoogleColaboratoryから保存した「pythondata02.ipynb」を開きます。
準備セルを実行
前回同様に、冒頭にコードが入力されています。
「import」はPythonで計算などが出来るように便利なライブラリをインポートするという意味です。また、変数pytableの中身をゼロクリアする記述があります。次に変数pytableに先ほどの「pythondata02.csv」のデータを入れ込む記述となっています。そして「print(pytable)」は変数pytableの内容を表示する記述です。
まずこのコードが書かれた1番目のセルを実行します。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# インライン宣言
%matplotlib inline
pytable = 0 #変数の中身ゼロクリア
pytable = pd.read_csv('pythondata02.csv', encoding="utf8")
print(pytable)
下のような実行結果となります。 
平均値
以下のコードを新しいセルにコピペして実行します。このコードの出力結果は金額(支出)と気温データの平均値が表示されます。
pytable.mean()
実行結果>>>
金額(支出) 3377.75
気温℃ 10.45
dtype: float64
dtype: float64と書かれているのは、平均値を表示する際に小数点以下の値を表示することとなり、そのために「float」というデータ型になったことを示しています。
中央値
中央値とは、代表値の一つで、データを小さい順に並べたとき中央に位置する値のことです。
例えば5人の年齢の中央値は、3番目に年老いている人となります。ただしデータ個数が偶数個の場合、中央に近い2つの値の算術平均をとります。中央値の事を、メディアン、メジアン、中間値とも言います。
以下のコードを新しいセルにコピペして実行します。このコードの出力結果は金額(支出)と気温データの中央値が表示されます。
pytable.median()
実行結果>>>
金額(支出) 780.0
気温℃ 11.0
dtype: float64
最頻値
最頻値はモード(mode)とも言われます。データ群や確率分布で最も頻繁に出現する値です。離散分布の場合は確率関数が,連続分布の場合は密度関数が,最大となる確率変数の値であり、分布が多峰性の場合は,それぞれの極大値を与える確率変数の値だと日本工業規格で定義されています。
以下のコードを新しいセルにコピペして実行します。このコードの出力結果は金額(支出)と気温データの最頻値が表示されます。
pytable.mode()
実行結果は下のようになります。 
分散(variance)
分散は統計以外ではあまり聞かない言葉だと思います。統計学において分散はほぼ言葉通り、数値データのばらつき具合を表すための指標です。
ある一つの数値データ群において、平均値と個々のデータの差の2乗の平均を求めることによって計算され、平均値から離れた値をとるデータが多ければ多いほど、分散が大きくなります。
以下のコードを新しいセルにコピペして実行します。このコードの出力結果は各金額と気温データの分散値が表示されます。
pytable.var()
実行結果>>>
金額(支出) 1.166189e+08
気温℃ 3.023077e+00
dtype: float64
これまでとは違い、実行結果を見ただけでは分散は何のことか分りません。分散の計算結果には「計算された数値が、小さいほどデータのばらつきが少ない」ということが言えるのですが、数値だけでは説得力に欠けます。
分散とは、ばらつき具合のことですので、これはやはり視覚的にグラフで見た方が良さそうです。
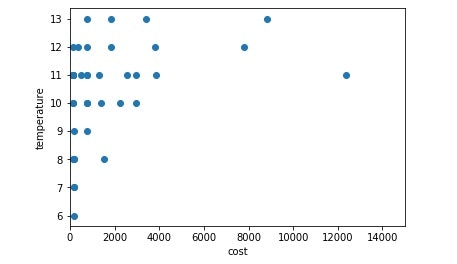
以下のコードを新しいセルにコピペして実行します。このコードの出力結果は縦軸を気温、横軸を金額(支出)としてグラフ表示されます。
from pandas.plotting import scatter_matrix
pytable.describe() #descriveメソッドで各列ごとの要約統計量を取得
plt.scatter(pytable['金額(支出)'], pytable['気温℃']) #scatterメソッドで散布図を描画
plt.xlim([0,15000]) #横軸xの下限を「0」、上限を「15000」
plt.ylabel('temperature') #縦軸ラベルを「temperature」
plt.xlabel('cost') #「縦軸ラベルを「cost」
plt.show() #コードの実行結果の表示
上のプロット図から、気温が高いときに、お金を使う傾向があるようにも見えます。こういった傾向はプロット図によって視覚化されることで判断できることもありますが、データ量が少なかったり適切でないデータ(誤記や、上限指定で除いた家賃などの気温とは無関係のデータ)はデータクレンジングで取り除く必要があります。
ただしデータクレンジングは慎重におこなう必要があり、誤記や重複、無関係だとする判断は議論が必要なときもあります。
おまけ
分散の求め方は以下となります。
①各データの平均値との差を求める
②その差をそれぞれ2乗する
③全ての求めた数値を足す
④最後にデータの数で割る
Pythonではコード内のvar()メソッドが裏で①~④を行ってくれていました。分散の公式は以下となります。
$$s^2 = \frac{1}{n}\displaystyle \sum_{ i = 1 }^{ n } (x_i-\overline{x})^2$$
上記式の説明をすると、$n$が観測値の数、$x_1,x_2…x_n$が一つ一つの観測値。$x$の添字は観測したデータの番号を表しています。$\overline{x}$はこれらの観測値の平均です。
※これは必要なときがくればおそらく、自ずと調べることになりますので、スルーしてもOKです。
標準偏差
標準偏差とは上記分散式の平方根をとることによって計算される値のことです。学生時に試験のときに耳にするあの偏差値の元となります。
ここでは、標準偏差を扱うにあたり、コードの実行は行わず説明にとどめることにします。
理由のひとつは、PythonライブラリのNumpyとPandasで実行結果が異なるため内容が詳細になってしまうためです。
そのため、標準偏差とは何だったかな、ということだけ書きます。
偏差という言葉は耳にします。試験の点数による偏差値とは、その値のあたりにどれくらいの人数がいるよ、といったことがわかる指標でした。中央値が50としておよそ端にいくほど人数が少なくなるような図が想像できます。
つまり、標準偏差とは、
”平均値±標準偏差値の中に大体の人(値)がいる”
ということが言えます。
おまけ
何故、標準偏差を求めるかというと、標準偏差の値が、工場生産の統計的品質管理の指標になったりするためです。
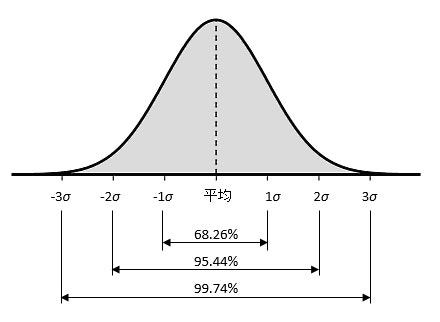
そのための正規分布における標準偏差が下図のようになります。
これは正規分布のグラフにおける、標準偏差(σシグマ)(1σ,2σ,3σ)が示す範囲を指しています。
上図の正規分布の場合、平均値±標準偏差$1σ$には、観測データが含まれる確率は68.26%になります。生産品質管理で大量生産するなか、±3σ(99.74%)より外の範囲の寸法誤差製品が出てしまうことなどが確率的に想定されたりします。
次回は外部データの取得か、機械学習について書く予定です。