はじめに
tacotronを学んでいくうちに出会ったGriffin-Limアルゴリズムについての備忘録
短時間フーリエ変換(stft)
Griffin-Limアルゴリズムを学ぶ前に短時間フーリエ変換の知識が必要になるので解説します。(自分はこんなものかと考えているため間違っていたら教えてください・・)
フーリエ変換は波形に対してどの周波数成分がどのくらい含まれているかを分析する手法です。
波形がどのような三角関数で表されているのかがわかります。つまりどんな波形も三角関数を足し合わせれば再現できます。
短時間フーリエ変換は波形に対してフーリエ変換の範囲と移動幅を決め短い区間でフーリエ変換を移動幅の分だけ繰り返す手法です。(うまく伝わるかな?)
時間的に変化する周波数成分を捉えられることがメリットです。
例えば、歌にフーリエ変換を用いても今までのメロディーとは全く異なるcパートが入るとそれも合わせてフーリエ変換してしまいます。
短時間フーリエ変換を上記の例に施してあげれば時間的に変化する周波数成分(aパートやbバートやcパート、移動幅を小さくすればパートの更に細かいところ)を捉えられます。
etc
短時間フーリエ変換は、移動幅を小さくしすぎると時間成分はいいもの周波数成分が悪くなってしまい、移動幅を大きくしすぎると今度は周波数成分はいいものの時間成分が悪くなってしまいます。これを不確定性原理といいます。
短時間フーリエ変換の実装
実装ではpytorchを使っていきます。pytorchのインストール方法についてはここで書くと長くなってしまうので省略します。
pytorchでは短時間フーリエ変換を1行で実装できます。
以下の形でpytorchの短時間フーリエ変換が提供されています。
以下実装です。
def STFT(data, n_fft):
stft = torch.stft(
input=data,
n_fft=n_fft
)
return stft
torch.stft()では移動幅はデフォルトだと短時間フーリエ変換をしてあげる幅の1/4に設定されています。
戻り値の形はTensor型です。
逆短時間フーリエ変換(istft)
短時間フーリエ変換には逆変換があります。それが逆短時間フーリエ変換です。
逆短時間フーリエ変換の実装
pytorchでは逆短時間フーリエ変換について以下の形で提供しています。
これを用いて実装します
def ISTFT(data, n_fft):
istft = torch.istft(
input=data,
n_fft=n_fft
)
return istft
これで実装ができました。
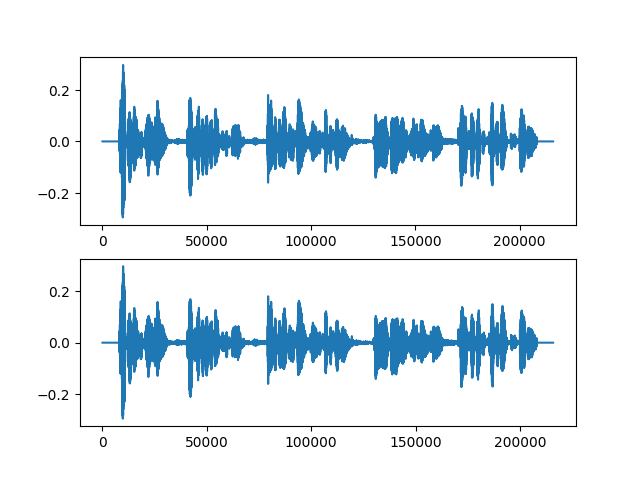
これだけだと本当に逆変換ができたのか分かりづらいので短時間フーリエ変換前と短時間フーリエ変換後の波形を見てみましょう。
filepath = 'data/audio.wav'
audiodata ,sr = torchaudio.load(filepath)
# 入力されたデータの波形の確認
fig = plt.figure()
a1 = fig.add_subplot(211)
a1 = plt.plot(audiodata.t().numpy())
if __name__ == '__main__':
#短期間フーリエ変換を施してあげる幅はとりあえず400にする
stft = STFT(audiodata,400)
istft = ISTFT(stft,400)
#逆変換されたデータの波形の確認
a2 = fig.add_subplot(212)
a2 = plt.plot(istft.t().numpy())
plt.show()
自分はLJSpeechの適当な音声のデータを入れてあげました。
結果は以下です。
上は、短時間フーリエ変換を施してあげる前
下は、逆短時間フーリエ変換を施してあげた後
ほとんど同じになりました。しっかり逆変換できて元の波形に戻っているようです。
Griffin-Limアルゴリズムとは?
前置きが長くなりましたが本題です。
はじめにで少し述べたTTSモデルのtacotronはテキストから振幅スペクトログラムを予測します。予測した振幅スペクトログラムを逆短時間フーリエ変換で音声にしたい場合、位相の情報が足りません。そこで位相を予測するためのアルゴリズムとしてGriffin-Limアルゴリズムが登場します。
Griffin-Limアルゴリズムは振幅スペクトログラムから位相をランダム(乱数を用いて)に初期化します。その後は以下の3つのステップを繰り返します。
(1)逆短時間フーリエ変換で振幅スペクトログラムとランダムに生成した位相スペクトログラムから波形を生成。
(2)その波形に短時間フーリエ変換を施す。
(3)(2)で得た振幅スペクトログラムを元の振幅スペクトログラムに置き換える。
これを繰り返すことでスペクトログラムの無矛盾性から位相が得られます。
十分に繰り返すと品質の良い結果が得られます。
実装
pytorchではGriffin-Limアルゴリズムについて以下の形で提供しています。
これを用いて実装します。
def GL(audiodata,sr,n_fft,n_iter):
#torchaudio.transforms.GriffinLimのデフォルトに沿ったパラメータ
win_length=n_fft
hop_length=win_length // 2
#Griffin_Limアルゴリズムの入力となるスペクトログラムの作成
spec = torchaudio.transforms.Spectrogram(
n_fft=n_fft,
win_length=win_length,
hop_length=hop_length,
)(audiodata)
#Griffin-Limアルゴリズム本体
griffin_lim = torchaudio.transforms.GriffinLim(
n_fft=n_fft,
#n_iterはGriffin-Limの3つのステップ反復回数、デフォルトは32
n_iter=n_iter,
win_length=win_length,
hop_length=hop_length,
)
outaudio = griffin_lim(spec)
return outaudio
これで実装できました。実際に動かしてみましょう。
filepath = 'data/audio.wav'
audiodata ,sr = torchaudio.load(filepath)
# 入力されたデータの波形の確認
fig = plt.figure()
a1 = fig.add_subplot(211)
a1 = plt.plot(audiodata.t().numpy())
if __name__ == '__main__':
#反復回数はデフォルトの32でいれてみる
gl = GL(audiodata,sr,400,32)
#Griffin-Limアルゴリズムでスペクトルから復元されたデータの波形の確認
a2 = fig.add_subplot(212)
a2 = plt.plot(gl.t().numpy())
plt.show()
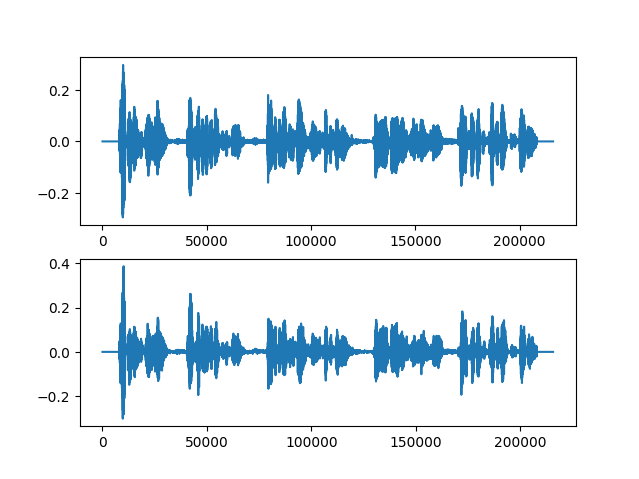
動かしてみた結果が以下です。
上が元の音声波形で下がGriffin-Limアルゴリズムで復元した波形です。
ちょっと違うのがわかるでしょうか?
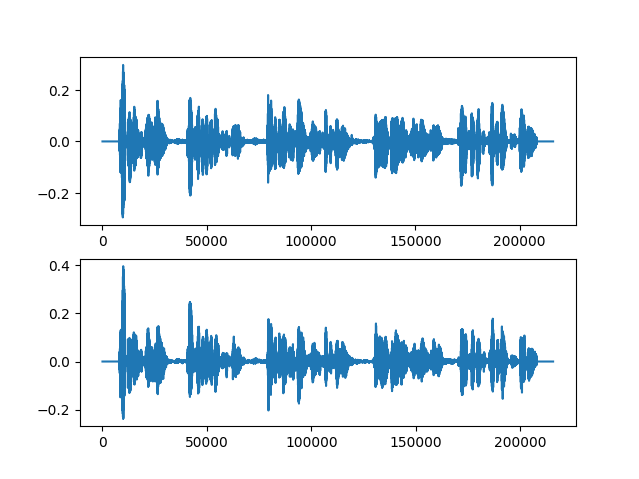
反復回数を10倍にしてみた結果は以下です。
10倍にする前よりはよくなった・・・のかな?
Griffin-Limアルゴリズムの現在
ここまで話したら、tacotronでGriffin-Limアルゴリズムを使っているのだろうとお思いでしょうがそうではありません。
Griffin-Limアルゴリズムの紹介で「十分に繰り返すと品質の良い結果が得られます」と記載しましたがそれは反復回数ごとの話です。
十分に反復回数を増やしたところで実際に聞いてみるとあまり良くない結果が返ってくることもあります。
現在、スペクトログラムから音声の変換ではwavenetをはじめとするニューラルボコーダが品質が良く、tacotronでもニューラルボコーダがスペクトログラムから音声波形の変換に用いられています。
実用的にこのGriffin-Limアルゴリズムは品質が問題視されないところで用いられているのが現状です。
おわりに
ニューラルボコーダを学んでいるうちにであったGrifin-Limアルゴリズムについてまとめてみた。
おもいつきでまとめてみたため勘違いもいっぱいありそう。(いつも知識の勘違いで教授に怒られている・・)
初心者であるため間違いが多少あるかもしれません。もし、間違えているところがありましたらこっそり教えてください。
この記事が誰かのお役に立てれば幸いです。
参考
短時間、逆短時間フーリエ変換、メルスペクトログラム、Griffin-Limアルゴリズムについては以下を参考にしました。特に「pythonで学ぶ音声合成」は音声を学ぶ上ですごくお世話になっています。音を学ぶ際にはぜひ読みたい一冊だと思います。興味があればぜひ。
山本 龍一、 高道 慎之介.pythonで学ぶ音声合成.インプレス.2021
https://book.impress.co.jp/books/1120101073
高道 慎之介、齋藤 佑樹、高宗 典玄、北村 大地、猿渡 洋.von Mises分布DNNに基づく振幅スペクトログラムからの位相復元.情報処理学会研究報告.2012
http://sython.org/papers/SIG-SLP/takamichi1806slp_paper.pdf