概要
世の中いろいろと気になることがありますが、やはりもっとも気になるのは「野球選手が本塁打を一番打てるのは何歳のときなのか」だと思います。今回は、メジャーリーグのデータから、ベイズ推定で打者の年齢ごとに本塁打率を求めたいと思います。本当の定義は違いますが、ここでは簡単のため「本塁打率 = 本塁打数 / 打数」と定義します。すなわち、本塁打率とはある選手が打席に立ったとき、(四球の場合などは除いて)どれくらいの確率で本塁打を打ってくれるかという値です。
使うツールは、
- Python
- Pandas
- Stan (PyStan)
です。
想定している読者は野球・ベイズ統計・Python・Stanのうちいくつかについて興味を持っていたり勉強している人です(そんな人はほぼいないし、逆にいたらこんな記事は読む必要がないんではという懸念がある)。そのため、それぞれについて詳しい説明はしませんが、適宜いい感じの文献を挙げたいと思います。
Excuse
私は統計の素人 && ベイズ推定の素人 && Stanの素人なので、以下の内容には根本的なものから細かいものまで様々な種類の間違いが含まれている可能性があります。よろしくお願いします(?)。
データの取得
Lahman's Databaseというありがたすぎるサイトでメジャーリーグのここ100年くらいのすべての選手の年ごとの成績(打数、安打数、三振数、本塁打数...)がまとまったファイルが公開されているので、使います。今回は2016年版のcsvファイル(「Download 2016 Version」 → 「2016 – comma-delimited version」)をダウンロードしてきます。
ダウンロードしたファイルを展開すると無限にcsvファイルがあるのでやる気が失せそうになりますが、今回使うのは
- Master.csv(選手の基本的な情報)
- Batting.csv(打撃成績)
のみです。
データの前処理
今回使うライブラリをimportして、csvファイルを読み込んでpandas.DataFrameにします。PandasというのはPython上で使えるめちゃくちゃ便利なExcelみたいなライブラリのことで(適当)、データを表の形で持ったり、そのデータに対して細かい操作をする上で非常に役立ちます。
import numpy as np
import pandas as pd
import pystan
import matplotlib.pyplot as plt
bat = pd.read_csv('Batting.csv')
mas = pd.read_csv('Master.csv')
Batting.csvの1つの列は一人の選手のある一年の打撃成績です。だいたいどんな形をしているのかを見てみます。
bat.tail()

なるほど〜、いい感じですね。年と選手のidにいろいろな成績が紐づいています。ただ、今回知りたいのは年齢と成績の相関なので、年齢の列を付け足してあげる必要があります。実は、Master.csvでは選手のidと生まれた年が並んでいるので、これを使ってあげます。Master.csvの形を見てみましょう。
mas.tail()

OK。選手のidをキーとして、二つのDataFrameをマージします。その後、シーズン年からその選手の生年を引き算することで選手の年齢を算出します。ただし、メジャーリーグではあるシーズンの選手の年齢は6月30日時点でのものを公式に使っているので、生まれた月が7月以降の選手については生年を翌年にしておきます。
mas['birthYear'] = mas['birthYear'] + (mas['birthMonth'] >= 7)
bat = pd.merge(bat, mas[['playerID', 'birthYear']], on='playerID')
bat['age'] = bat['yearID'] - bat['birthYear']
ちなみに、上記の年齢の話のような野球の統計学をする上でのTIPSや、いろいろな分析結果が載っている本として、以下の2冊を挙げておきます。
それでは分析をしていきますが、あまりに昔すぎるデータや、少ししか出場していない選手のデータを使うのはあまりよくなさそうなので、今回はデータフレームからけずることにします。具体的には、1965年以降に生まれていて、かつ通算で1000打席以上立っている選手のデータのみ使います。そのために、まず打席数(PA)を算出した後、groupbyを使ってその選手の通算打席を出すという処理をしています。
bat['PA'] = bat['AB'] + bat['BB'] + bat['HBP'] + bat['SH'] + bat['SF']
pa_c = bat.groupby('playerID').sum()[['PA']]
pa_c.columns = ['PA_Career']
bat = pd.merge(bat, pa_c, left_on='playerID', right_index=True)
ここで一旦、DataFrameの様子を見てみましょう。
bat.head()

右の方に選手の年齢の列が追加されていて、いい感じですね。それでは、実際の分析をしてみます。
モデル0(平均値) & なぜベイズ推定の必要があるのか
以下、最初は簡単なモデルからはじめて、徐々にいい感じにアップデートしていくものとします。
まずは一番簡単に、年齢ごとにすべての選手の打席数と本塁打数を合計して、割り算するということをやってみたいと思います。たとえば、「データに含まれる30歳の選手の打数を合計すると100000打席で、そのうち本塁打を3000本打ったとすると、30歳の選手の本塁打率は3000 / 100000で0.03である」、というような計算をします。このような処理はPandasのgroupbyの機能を使うと非常に簡単に行うことができます。
HRdf = bat.groupby('age').sum()[['AB', 'HR']]
HRdf['HRR'] = HRdf['HR'] / HRdf['AB']
fig, ax = plt.subplots()
HRdf['HRR'].plot(kind='line', style='o-', c='black', ax=ax)
ax.set_ylabel('p')
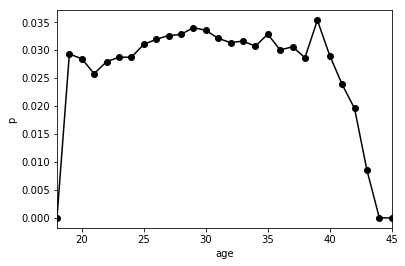
横軸が年齢、縦軸が本塁打率です。なるほどという感じですね。19歳から本塁打率はゆっくり上昇傾向にあり、29歳でもっとも高くなることがわかります。その時の値は0.034、すなわち3.4%程度です。その後はゆっくり下降し、40歳以降で急激に低下しています。
ということで、年齢ごとの本塁打率がわかってめでたい、ということで終わっても良いのですが、上記のグラフを「真の本塁打率」と考えてしまうことには問題がありそうです。
(a). **個人差が考慮されていない。**この図では37,8歳の選手が20代後半の選手と同じくらい本塁打を打てることになっているのですが、これは本当でしょうか。冷静に考えると、これは30代後半になってくると、打撃成績が良くない打者は引退してしまい、比較的本塁打が打てる打者のみが残っているせいではないかと思えてきます。そのような、30代後半まで現役でいられるような打者は20代後半ではもっと本塁打を打っているはずなのに、それは今回の図からはわかりません。これは、すべての打者を平均してしまっているため個人差が考慮されていないことが原因です。
(b). **ノイズが大きい。**上の図では39歳の打者が異常に本塁打を打っていますが、これは、野球選手が39歳になった瞬間本塁打を打つ能力が急に上がるということを意味してはいないでしょう。39歳になったからといって急に本塁打を打てるようになる理由がとくに思いつかないからです。普通に考えて、39歳の選手の野球選手の真の能力は、37歳や38歳とほぼ同じか、少しそれらよりも衰えているはずです。
(c). **データ点の信頼度がわからない。**上記のデータにおいて30歳の打者と45歳の打者では数がまったく違います。今回のような全体の平均をとるような処理をした場合は、サンプル数が多いほど値の信頼度が高まるので、45歳のデータというのはほとんど信頼できない(真の値に近い値を表している可能性が低い)わけです。それにも関わらず、30歳のデータと堂々顔で並んでいるのはおかしいという気がします。
以上のような理由から、統計モデリングをしていきたいという気持ちになります。上記は私(素人)の考えなので、統計モデリングの利点や基本的な考え方を学びたい場合は、例えば以下の本を読むと良いと思います。
モデル1(年齢を考慮した階層ベイズ)
以下のようなモデルを立ててみます。
$$HR[i] \sim \mathrm{Binomial}(AB[i],p[i]), \\
p[i] = \mathrm{Logistic}(β+r_{age}[age[i]]), \
r_{age}[j] \sim \mathrm{Normal}(0,s_{age})
$$
急に意味不明な式を出してしまったので、日本語で説明します。あるシーズンのある打者の本塁打数は、打数$AB$と本塁打率$p$で決まる二項分布に従うとします。さらに、その本塁打率$p$は、定数$\beta$とその選手の年齢できまる変数$r_{age}$の和を引数とするLogistic関数表されるとします。ここで、各年齢に対する$r_{age}$の値は平均0、分散$s_{age}$の正規分布に従います。いまから、MCMCができるフリーソフトStanのPythonのラッパーであるPyStanを使って、それぞれのパラメータをベイズ推定していきます。
ここで、ベイズ推定とはなにか、MCMCとはなんなのか、Stanはどうやって使うのか、確率分布とはいったいなんなんだ、そもそも人はなぜ生きるのか、人間の意識はどのように生まれたのか、AIも意識を持ちうるのか、ということをいちいち述べていくと完全に日が暮れてしまう上に私よりもちゃんとした人の説明が世の中にいっぱいあるので、ここでは説明しません。
日本語で比較的簡単に読めそうな書籍だと、ベイズ推定や統計モデリングに関する基礎的なことは上記で挙げた「データ解析のための統計モデリング入門」が、Stanについては「StanとRでベイズ統計モデリング」を読めばだいたいわかると思います。
PyStanのコードは以下です。
AB = bat['AB'].values
HR = bat['HR'].values
age_map = {age: idx+1 for idx, age in enumerate(np.unique(bat['age'].values))}
age = bat['age'].map(age_map).values.astype(int)
data = dict(N=len(AB), N_age=len(np.unique(age)), HR=HR, AB=AB, age=age)
model_code = """
data {
int N;
int N_age;
int HR[N];
int AB[N];
int age[N];
}
parameters {
real beta;
real<lower=0> s_age;
vector[N_age] r_age;
}
transformed parameters {
vector[N] p;
for (i in 1:N)
p[i] = inv_logit(beta + r_age[age[i]]);
}
model {
r_age ~ normal(0, s_age);
HR ~ binomial(AB, p);
}
generated quantities {
real p_age[N_age];
for (i in 1:N_age)
p_age[i] = inv_logit(beta + r_age[i]);
}
"""
fit = pystan.stan(model_code=model_code, data=data, chains=4, iter=1000)
上記のコードを実行すると、計算機ががんばってくれて、いろいろなパラメータ($\beta, s_{age}, r_{age}$)の分布が得られます。ベイズ推定ではパラメータの値がある1つの値に定まるのではなく、分布として得られるのでデータの不確定性を表すことができます。たとえば、45歳のデータは30歳のものとくらべてサンプルが少なく不確定なので、パラメータの分布が広がることになります。すなわち、上で説明したデータの平均をとるだけの解析の問題点(c)が解決することになります。
結局推定したいのは、年齢ごとの本塁打率$p$なので、$r_{age}$とともに以下のコードでプロットしてみます。
def plot_r_p(fit):
inv_age_map = {v: k for k, v in age_map.items()}
x_age = [inv_age_map[a] for a in np.unique(age)]
r_age_trace = fit.extract()['r_age']
p_age_trace = fit.extract()['p_age']
# 中央値と50%・95%予測区間をプロットするため以下の点でのpercentileを計算
percents = [2.5, 25, 50, 75, 97.5]
r_age = []
p_age = []
for percent in percents:
r_age.append(np.percentile(r_age_trace, percent, axis=0))
p_age.append(np.percentile(p_age_trace, percent, axis=0))
fig, axs = plt.subplots(nrows=1, ncols=2, sharex=True, figsize=(12, 4))
# axs[0] : r_age
axs[0].plot(x_age, r_age[2], 'o-', color='blue') # 中央値
axs[0].fill_between(x_age, r_age[0], r_age[4], alpha=0.1, color='blue') # 95%区間
axs[0].fill_between(x_age, r_age[1], r_age[3], alpha=0.3, color='blue') # 50%区間
axs[0].set(xlabel='age', ylabel=r'$r_{age}$')
# axs[1] : p_age
axs[1].plot(x_age, p_age[2], 'o-', color='red')
axs[1].fill_between(x_age, p_age[0], p_age[4], alpha=0.1, color='red')
axs[1].fill_between(x_age, p_age[1], p_age[3], alpha=0.3, color='red')
axs[1].set(xlabel='age', ylabel=r'$p_{age}$')
return fig, axs
fig, axs = plot_r_p(fit)
HRdf['HRR'].plot(kind='line', style='o-', c='black', ax=axs[1]
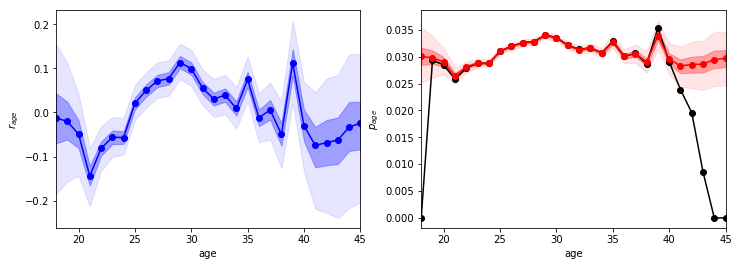
左の青色のデータが$r_{age}$、右の黒色のデータは上で示した単純な平均値、赤色のデータが推定された年齢ごとの本塁打率$p_{age}$です。いずれのグラフでも、薄い背景色が50%予測区間、濃い背景色が95%予測区間を表しています。
ということで、結果を見てみるとうーんという感じがしますね。問題点(c)はたしかに部分的に解決したと思いますが、(a)の個人差の問題と(b)のノイズの問題については何もできていません。たとえば、相変わらず39歳で急に本塁打を打てることになっていますし、さらに新たな問題としてデータ点が少ない40代以降で能力が向上するという、現実的とは考えづらい結果になっています(これは、たぶん全年齢の平均に近づいた方が尤度が高くなるせいだと思います)。
モデル2(時系列を考慮)
以上の問題を解決するため、時系列を考慮することにします。どういうことかというと、前のモデルでは年齢ごとの能力を完全に独立に扱っていました(モデル1の式で$r_{age}$が平均0の正規分布に従っていることに対応します)。しかし、よく考えるとj歳での能力というのは(j-1)歳での能力と近いものになるはずです。このことをモデルに反映させてあげると、以下のようになると思います。
$$HR[i] \sim \mathrm{Binomial}(AB[i], p[i]), \
p[i] = \mathrm{Logistic}(\beta + r_{age}[age[i]]), \
r_{age}[j] \sim \mathrm{Normal}(r_{age}[j-1], s_{age}), \
\sum_{j} r_{age}[j] = 0$$
このモデルでは、$r_{age}[j]$が従う正規分布の平均が$r_{age}[j-1]$になっていますね。これが、「j歳での能力は(j-1)歳での能力と近いものになるはず」という仮定を表しています。
AB = bat['AB'].values
HR = bat['HR'].values
age_map = {age: idx+1 for idx, age in enumerate(np.unique(bat['age'].values))}
age = bat['age'].map(age_map).values.astype(int)
data = dict(N=len(AB), N_age=len(np.unique(age)), HR=HR, AB=AB, age=age)
model_code = """
data {
int N;
int N_age;
int HR[N];
int AB[N];
int age[N];
}
parameters {
real beta;
real<lower=0> s_age;
vector[N_age] r_age;
}
transformed parameters {
vector[N] p;
for (i in 1:N)
p[i] = inv_logit(beta + r_age[age[i]]);
}
model {
r_age[1] ~ normal(-sum(r_age[2:N_age]), 0.001);
r_age[2:N_age] ~ normal(r_age[1:(N_age-1)], s_age);
HR ~ binomial(AB, p);
}
generated quantities {
real p_age[N_age];
for (i in 1:N_age)
p_age[i] = inv_logit(beta + r_age[i]);
}
"""
fit2 = pystan.stan(model_code=model_code, data=data, chains=4, iter=1000)
モデル1からの変更点は、modelでr_age[2:N_age] ~ normal(r_age[1:(N_age-1)], s_age)としてる部分のみです($r_{age}$の和を0にするためにr_age[1] ~ normal(-sum(r_age[2:N_age]), 0.001)としてる部分は本当は非常によくない気がする...)。
結果をプロットすると以下のようになります。
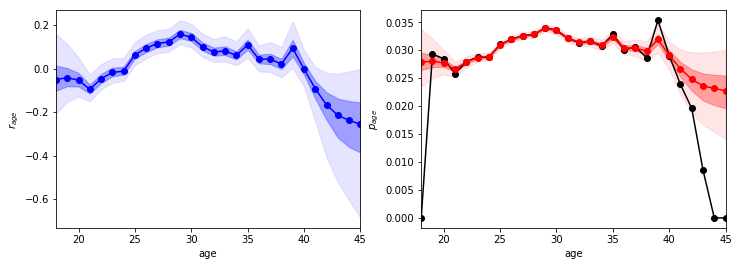
なるほど〜。モデル1と比べると良い点が2つあります。
- 39歳での能力の高まりが少し抑えられた。
- 40代での能力が年々下がるようになった
これはいずれも時系列を考慮した効果であり、かつ現実に即した結果であると考えられます。ということで、問題点(b)のノイズについて少しは改善した気がします。そこで、最後に個人差を考慮したモデルを作りましょう。
モデル3(個人差を考慮)
ということで、モデルに個人差を表す$r_{id}$という項を追加します。これは選手ごとの能力の差を表す変数で、平均0の正規分布に従うようにします。
$$HR[i] \sim \mathrm{Binomial}(AB[i], p[i]), \
p[i] = \mathrm{Logistic}(\beta + r_{age}[age[i]] + r_{id}[id[i]]), \
r_{age}[j] \sim \mathrm{Normal}(r_{age}[j-1], s_{age}), \
\sum_{j} r_{age}[j] = 0, \
r_{id}[j] \sim \mathrm{Normal}(0, s_{id})$$
id_map = {id: idx+1 for idx, id in enumerate(np.unique(bat['playerID'].values))}
id = bat['playerID'].map(id_map).values.astype(int)
data = dict(N=len(AB), N_age=len(np.unique(age)), N_id=len(np.unique(id)), HR=HR, AB=AB, id=id, age=age)
model_code = """
data {
int N;
int N_id;
int N_age;
int HR[N];
int AB[N];
int id[N];
int age[N];
}
parameters {
real beta;
real<lower=0> s_age;
real<lower=0> s_id;
vector[N_age] r_age;
vector[N_id] r_id;
}
transformed parameters {
vector[N] p;
for (i in 1:N)
p[i] = inv_logit(beta + r_age[age[i]] + r_id[id[i]]);
}
model {
r_id ~ normal(0, s_id);
r_age[1] ~ normal(-sum(r_age[2:N_age]), 0.001);
r_age[2:N_age] ~ normal(r_age[1:(N_age-1)], s_age);
HR ~ binomial(AB, p);
}
generated quantities {
real p_age[N_age];
for (i in 1:N_age)
p_age[i] = inv_logit(beta + r_age[i]);
}
"""
fit3 = pystan.stan(model_code=model_code, data=data, chains=4, iter=1000)
結果を見てみましょう。
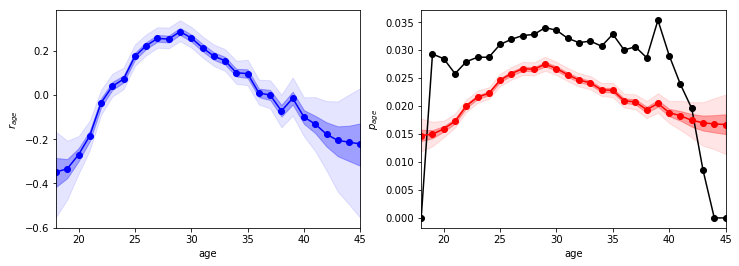
なるほど〜。これはかなりいい感じの結果ではないでしょうか。年齢が能力ごとに滑らかに変化しており、かなり妥当に見えます。ここで、$p_{age}$の推定値が実測値よりもかなり小さくなっていますが、これは推定値は「年齢ごとの平均的な選手の$p_{age}$」を表しているからだと思います。実測値ではすごい選手ほど打席が多くなると思うので、全体の平均をとるとすごい選手の比重がすごくない選手よりも高くなり、結果として平均的な選手の$p_{age}$よりもすごい値がでます。
結論としては、29歳の選手が一番本塁打を打つ確率が高く、平均的な選手で2.5%よりを少し上回る程度です。29歳の前後での能力の変化を見ると、29歳以前での成長の方が29歳以後の衰えよりも急な変化になっていることがわかりますね。また、例えばだいたい20歳前後での$p_{age}$が1.5%より少し高い程度なので、平均的には30歳前後の選手は20歳前後の選手よりも$(2.5 / 1.5) \simeq 1.7$倍くらい本塁打を期待できることになりますね。
まだいろいろとできると思いますが、とりあえずこの辺で、、、。
まとめ
ということで、PyStanを使ったベイズ推定で野球選手が本塁打を一番打てるのは何歳のときなのかベイズ推定した結果、29歳の選手が一番本塁打を打てることがわかりました。
以上、よろしくお願いします。
おまけ:他の指標についても同じように調査したのですが、さすがにそれを列挙するのはqiitaの趣旨からはずれる気がするので別( http://hoture6.hatenablog.com/entry/2017/06/08/212256 ) でまとめました。興味があればどうぞ。