機械学習ノート: スペクトラルクラスタリング(参考: The elements of statistical learning他)

#1. 要約
　通常のK-meansクラスタリングでは，重心からの距離によってクラス形成を行うため，クラスターの形状が超球状になります．本来のデータ構造が非凸集合である場合(e.g. 三日月型データetc.)は，誤分類が多くなってしまいます．そうした場合には，クラス形成をグラフカットによって達成しようとするスペクトラルクラスタリングが有用です．今回の記事では，スペクトラルクラスタリングについて，ざっくりと解説しました．こちらのqiita記事やこのスライドを参考にしているため，詳しくはこれらを見てください．
#2. グラフラプラシアン
グラフラプラシアンについては，この記事(グラフラプラシアンを噛み砕いて噛み砕いて跡形もなくしてみた)が詳しかったです．要約すると，グラフラプラシアンは，各頂点に何個の頂点が連結しているかを表す次数行列$D$と，頂点i,jが隣接している場合は1，そうでない場合は0という要素を持つ隣接行列$A$の差で定義される行列で，グラフの有用な性質を見つけるために利用される，と書かれています．
#3. ラプラシアン固有マップ法
　ラプラシアン固有マップ法は，サンプルからグラム行列を推定して次元圧縮する最も基本的なアルゴリズムです(赤穂,2008)．赤穂(2008)「カーネル多変量解析」に則り，以下のようにグラフの頂点間の重みを定義します．

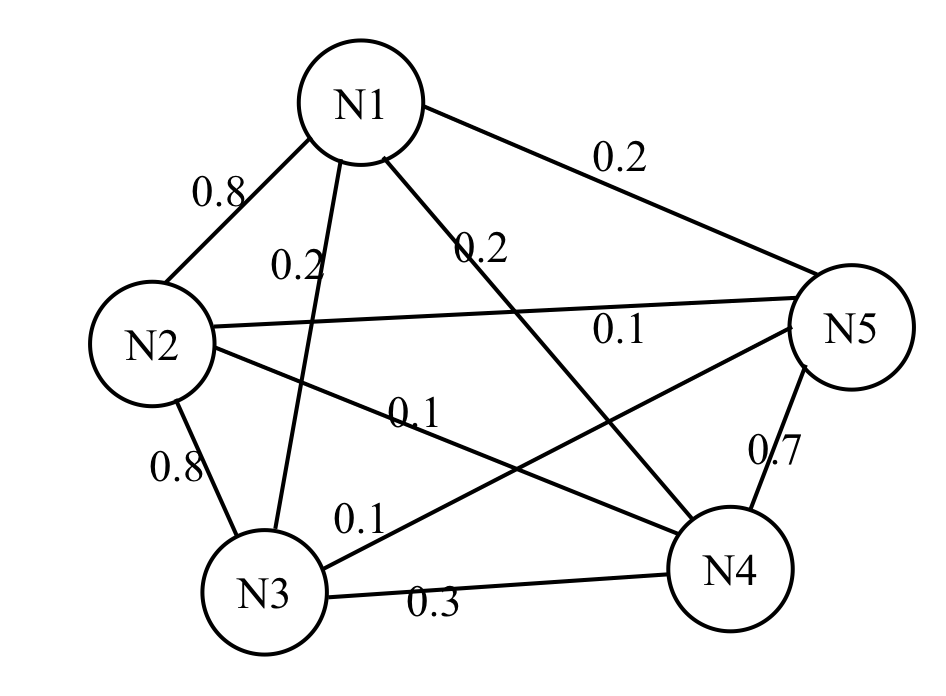
サンプルに対応するグラフの枝に重みをつけることを考える．互いに近いデータは大きな重みを，遠いデータは小さな重みとなるようにする．たとえば，データ空間$\mathcal{X}$が十数ベクトル空間であれば，ガウスカーネルを重みとして取ることが出来る．iとjを結ぶ枝の重み$K_{ij}$を成分とする行列を$K$とする．(赤穂, 2008)

たとえば，以下のようなグラフ

に対する重み行列は

\begin{eqnarray}
K=
\begin{pmatrix}
0&0.8&0.2&0.2&0.2\\
0.8&0&0.8&0.1&0.1\\
0.2&0.8&0&0.3&0.1\\
0.2&0.1&0.3&0&0.7\\
0.2&0.1&0.1&0.7&0
\end{pmatrix}
\end{eqnarray}

となります．ラプラシアン固有マップ法では，このようなデータ(頂点がデータ点です)間の重み付きの差を小さくすることで$i$番目のサンプルの表現$a_i$を決めることを目的とします．数式で書くと，以下のように表すことができます．

\begin{eqnarray}
\underset{a}{min} \sum_{i,j}K_{ij}(a_i-a_j)^2&=&2a^T(diag(\sum_jK_{ij})-K)a\\
&:=&2a^T(\Lambda-K)a:=2a^TPa
\end{eqnarray}

このaの関数を最小化することで，重み$K_{ij}$が大きいサンプルの表現同士は近くに配置されるということが達成されます．ここで$P=\Lambda-K$はグラフ上のラプラス作用素として知られているものです(赤穂,2008)．aの定数倍による不定性を解消するために，$$a^T\Lambda a=1$$という制約を課すと，ラグランジュ関数は，$$L(a) = a^TPa-\tau(a^T\Lambda a-1)$$となるので，これをaで微分して0と置くと，$$Pa = \tau\Lambda a$$となります．以上から，ラグランジュ関数の最小化は一般化固有値問題に帰着することがわかりました．よって解は，最小固有値に対応する固有ベクトルと一致することがわかります．ただし，固有値0に対応する固有ベクトルは$a\propto1$という自明な解であるので，固有値0を除いて，それより大きい最小固有値に対応する固有ベクトルをとりましょう．これでサンプルの低次元表現の計算過程がわかりました．
#4. スペクトラルクラスタリング
　スペクトラルクラスタリングは，グラフの枝をカットして分割する問題と考えられます．たとえば先ほどのグラフだと，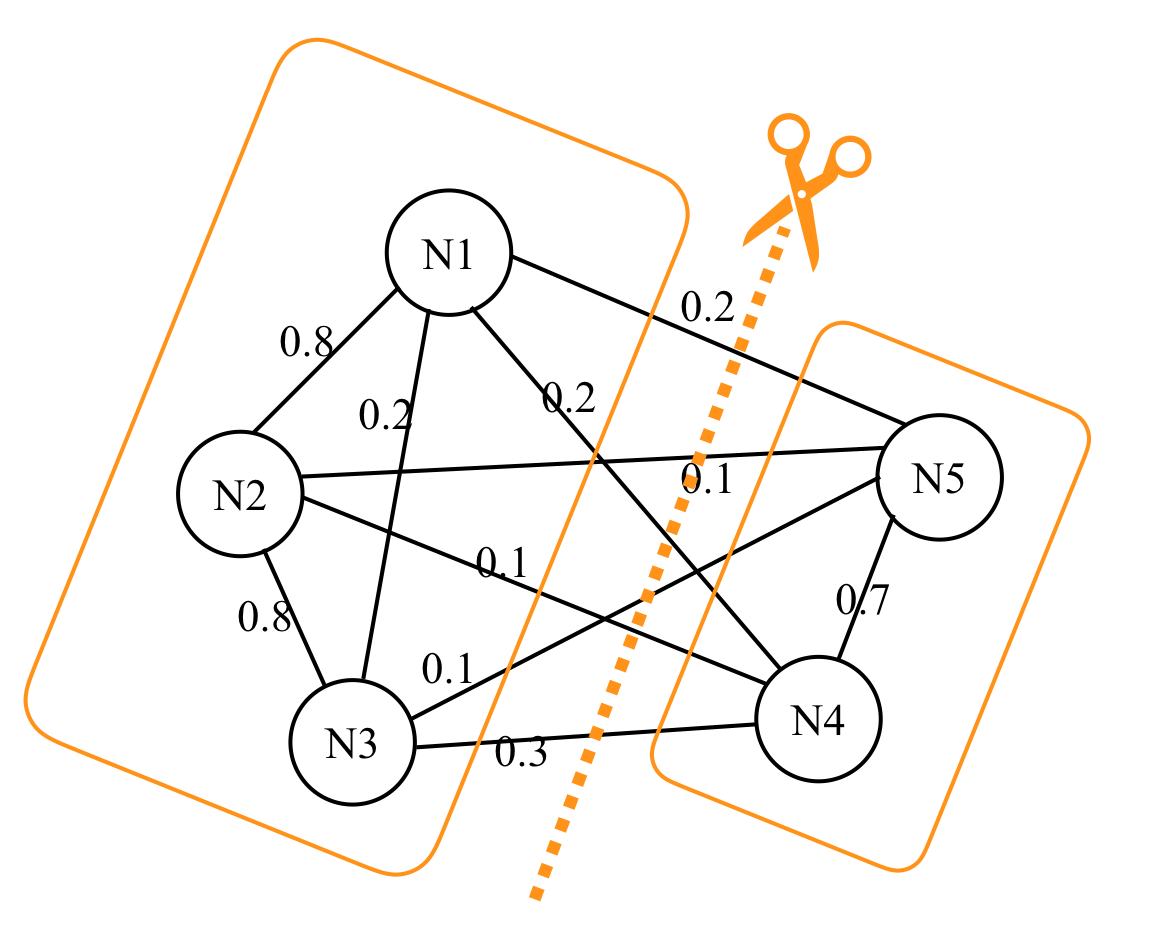
のように枝を切ることが考えられます．むやみやたらと枝を切っても仕方がないので，__カットする枝の重みが最小となるようにカットする__というのを念頭に置いて最適化問題を定式化します．赤穂(2008)では

グループ内はできるだけ近いものどうしが集まり，グループ間は遠く離れていることが望ましいから，このカットの重みの合計は小さいほどよい

と表現されています．これを数式で表すと，

\begin{eqnarray}
\underset{a}{min} \sum_{i,j}K_{ij}(a_i-a_j)^2=2a^TPa,\ \ a_i = \pm1
\end{eqnarray}

となります．これはラプラシアン固有マップ法に$a_i = \pm1$(サンプル$i$がどちらのクラスに属するか)の条件が加わったもので，この条件が加わったことで，整数計画問題となっています．整数計画問題は一般に解きづらいので，この離散値条件をなくすと，ラプラシアン固有マップ法と同様に一般化固有値問題に帰着します．よって0より大きい最小固有値に対応する固有ベクトルが，離散値条件を外した際の解となります．離散値条件を満たす解は，この固有ベクトルに対してクラスタリングを行うことで求めることができます．
　スペクトラルクラスタリングは，クラスターの形状が非凸でも，(近接行列を適切に生成できれば)うまくクラスター形成を行うことができます．試しに，以下のような三日月データに対する分類を見てみましょう．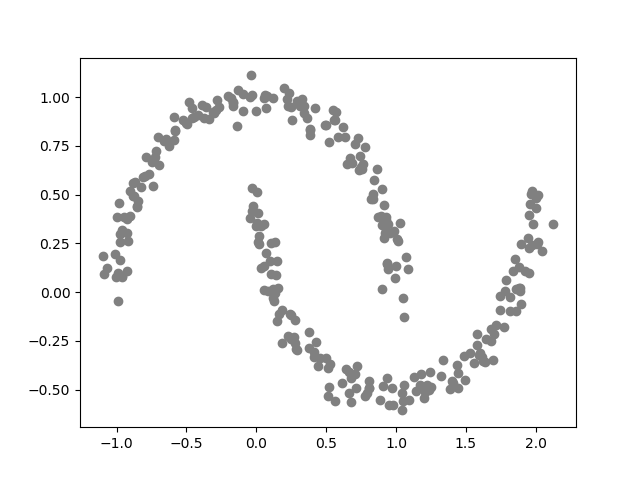
プロットして見ると，これは２つのクラスからなるデータだとわかりますが，数値のみのデータだとわかりません．このデータに対して，K-meansクラスタリングを適用してみると，以下のようになります．ここで，所属するクラスによって，点の色を変えており，十字はクラスター中心を表しています．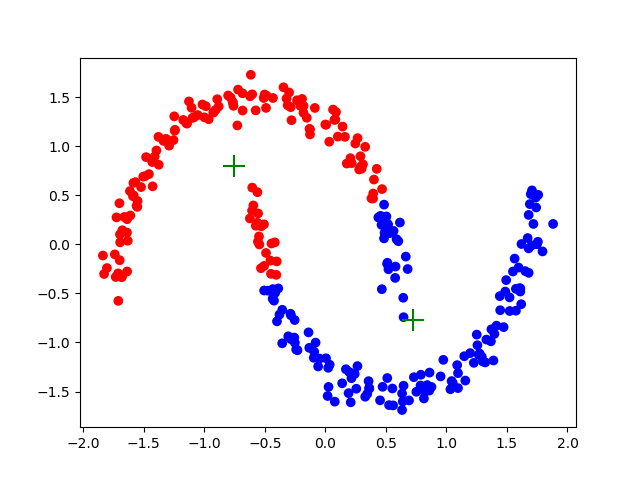
うまく分類できていませんね．これは，K-meansのアルゴリズムが各個体とクラスター重心(=セントロイド)との距離を計算し，その距離が最も短くなるクラスに個体を分類していることに起因しています．このような分類アルゴリズムだと，分類結果のクラスターはどうしても球状になります．これに対処するために，スペクトラルクラスタリングは，元のデータを何らかの情報を表現するように変換して，その後に，その情報に基づいてK-meansクラスタリングを行います．データの変換方法には，あるデータ点とその周囲のデータとの距離を用いる"k-nearest neighbor"やガウスカーネルを持ちる"radial basis function"など，様々な方法が存在します．いかにざっくりとしたスペクトラルクラスタリングのアルゴリズムを記述します．

---

<アルゴリズム(スペクトラルクラスタリング)>

• Step 1. データを変換の変換方法を決め，グラフ行列を作成する
• Step 2. グラフ行列を固有値分解して，大きい？小さい？方からいくつかの固有値を選び，グラフ行列の低次元表現を求める．たとえば固有値分解$G = VDV^T$に対して，$V_kD_k$のようにk次元での表現を計算する．
• Step 3. Step 2で得た低次元表現に対してK-meansクラスタリングを行う．(反復計算，多重スタートが必要．)

---

__データの情報がはっきりするように変換して，固有値分解によって意味のある情報の部分を抽出する__というのがポイントです！！以下に，スペクトラルクラスタリングによる三日月データの分類結果を示します．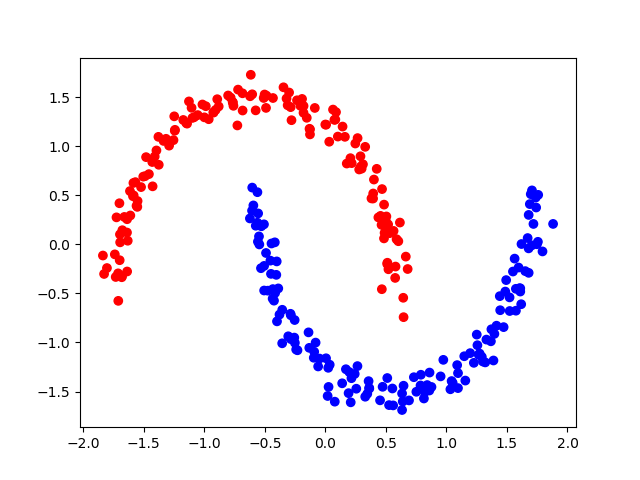
綺麗に分かれてる!素晴らしい!

#5. サンプルコード
今回は，K-means，Spectral Clusteringを実行するためにsklearn.clusterを使ってます．スクラッチで実装しようかと思いましたが，また他に勉強したいことができたので，今回はライブラリ様を利用しました．実装するなら，グラフ行列を計算する手続きの記述(特にnearest neighbor)がめんどくさそう．

{python3,clustering.py}

import numpy as np 
import matplotlib.pyplot as plt 
from sklearn import datasets as sd 
from matplotlib.colors import ListedColormap


data = sd.make_moons(n_samples=300,noise=0.05,random_state=0)
plt.scatter(data[0][:,0],data[0][:,1],c="gray")
#plt.savefig("適当なディレクトリ")
plt.show()
colors = ["red","blue"]
cmap_rb = ListedColormap(colors)

from sklearn import preprocessing as pp 
data_scaled = pp.scale(data[0])
plt.scatter(data_scaled[:,0],data_scaled[:,1],c=data[1],cmap=cmap_rb)
plt.show()


#clusterのドキュメント(https://scikit-learn.org/stable/modules/generated/sklearn.cluster.KMeans.html)
from sklearn import cluster
km = cluster.KMeans(n_clusters=2)
res_km = km.fit(data_scaled)
res_km.cluster_centers_ #セントロイド
res_km.labels_ #分類後のラベル
res_km.inertia_ #各クラスター中心とそのクラスターに属する点の二乗和
res_km.n_iter_ # 反復回数


plt.scatter(data_scaled[:,0],data_scaled[:,1],c=res_km.labels_,cmap=cmap_rb)
plt.scatter(res_km.cluster_centers_[:,0],res_km.cluster_centers_[:,1],s=250,marker="+",c="green")
#plt.savefig("適当なディレクトリ")
plt.show()

#spectral clustering(https://scikit-learn.org/stable/modules/generated/sklearn.cluster.SpectralClustering.html#sklearn.cluster.SpectralClustering)
spkm = cluster.SpectralClustering(n_clusters=2,affinity="nearest_neighbors")
res_spkm = spkm.fit(data_scaled)
res_spkm.affinity_matrix_ # kernel変換後の行列
res_spkm.labels_ #分類後のラベル

plt.scatter(data_scaled[:,0],data_scaled[:,1],c=res_spkm.labels_,cmap=cmap_rb)
#plt.savefig("適当なディレクトリ")
plt.show()

#まとめ
スペクトラルクラスタリングは，各データ点間のグラフ表現を求め，それを固有値分解したものをK-meansクラスタリングする手法だということがわかりました．ポイントは，__素データをデータ点間の距離を表すグラフ行列に変換し，その中でもクラスター形成に有用な情報を持つ部分を固有値分解で抽出する__という点です．最初のグラフ表現への変換でkernelを用いていた時は，何となく，カーネル主成分分析+K-meansクラスタリングの手法である，といった印象を受けます．
　

#参考文献
[Hasitie,Tibshirani,Friedman(2009).The elements of statistical learning]
(https://www.springer.com/jp/book/9780387848570)
赤穂(2008)「カーネル多変量解析」
量子アニーリングとスペクトラルクラスタリングの繋がり(qiita記事)
スペクトラル・クラスタリング(slideshare)
グラフラプラシアンを噛み砕いて噛み砕いて跡形もなくしてみた