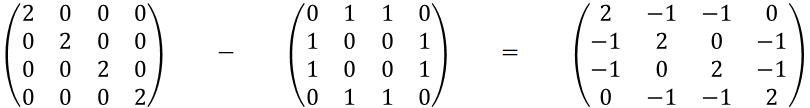はじめに
UL Systems Advent Calendar 2018 の3日目です。
最近グラフ理論を学び始めて覚えた言葉、グラフラプラシアンについて書きたいと思います。では、タイトルにもあるように、早速噛み砕いていきましょう。
グラフラプラシアンとは
まず、グラフラプラシアンは、ラプラシアン行列と同義です。
WikipediaのLaplacian matrixには、こう書かれています。
Laplacian matrix
In the mathematical field of graph theory, the Laplacian matrix, sometimes called admittance matrix, Kirchhoff matrix or discrete Laplacian, is a matrix representation of a graph. The Laplacian matrix can be used to find many useful properties of a graph.
つまり、
- ラプラシアン行列は、グラフ理論の数学的分野におけるグラフの行列表現である
- ラプラシアン行列は、グラフの有用な特性を見つけるために使用する
ということです。例えば、グラフを行列表現できれば、類似度に基づいたクラスタリングに応用することができます。
グラフとは
続いて、グラフについて触れます。ここでのグラフとは、頂点（Vertex）と辺（Edge）の集合です。統計のグラフではありません。グラフは、様々な問題や物事をモデル化したり視覚的に表現する場合で使用されます。一見、単純なデータ表現ですが、表現力豊かで柔軟なため、実世界の複雑な問題や物事でも直感的に表現することができます。具体的には路線図やネットワーク図等が例として挙げられます。
実世界でのグラフの例）路線図
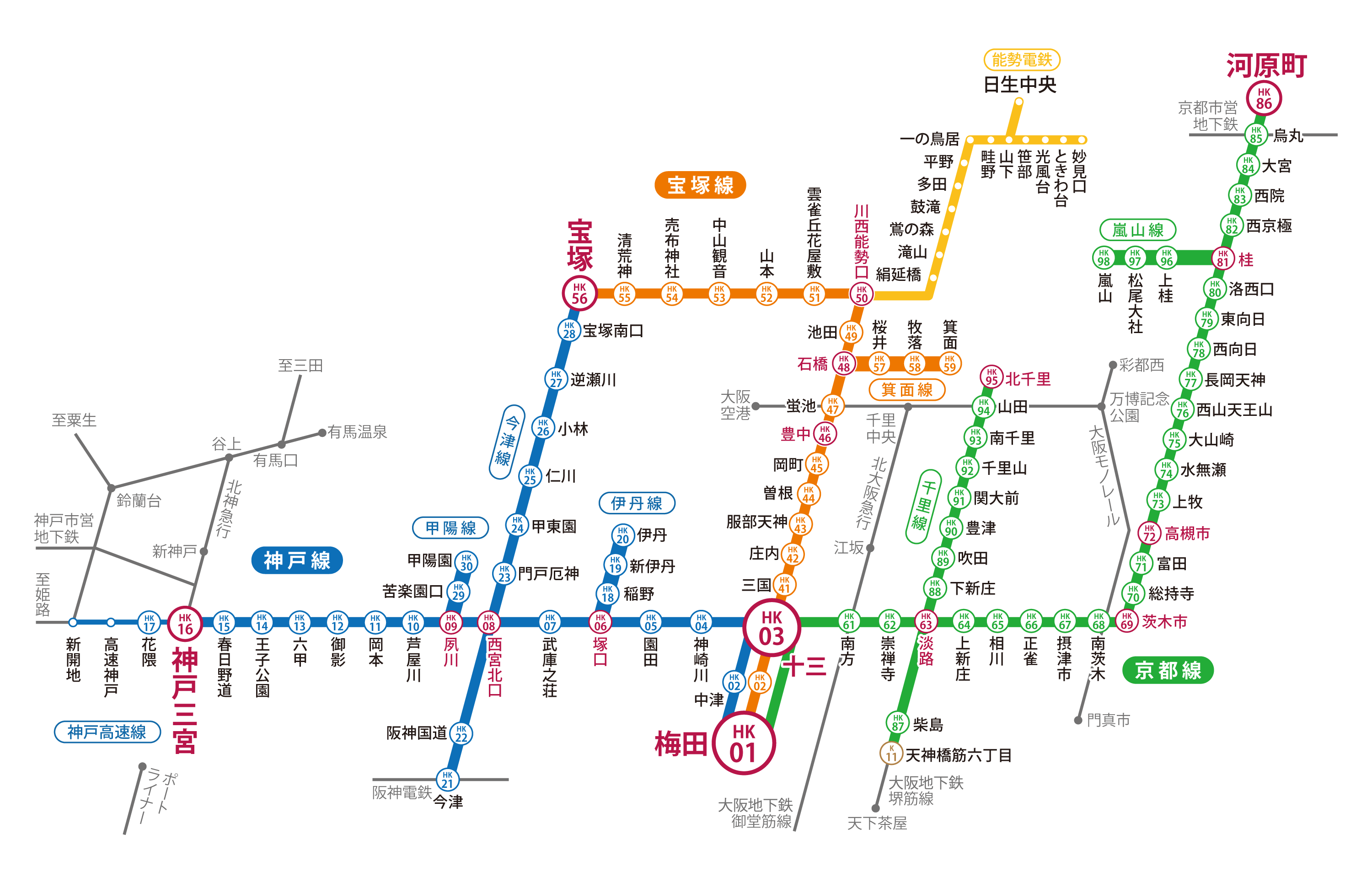
(引用:http://www.hankyu.co.jp/station/)
ラプラシアン行列
ここからは、以下のグラフを例に話を進めます。
それでは、具体的にラプラシアン行列とはどのような行列なのでしょうか。ラプラシアン行列は以下で定義されます。$L$はグラフラプラシアン、$A$は隣接行列、$D$は次数行列です。
$$L=D-A$$
隣接行列
行も列もグラフの頂点に対応します。辺がある頂点は1、辺がない頂点は0として表現します。そのため、対称行列になります。例のグラフの場合、隣接行列$A$は次の行列で表すことができます。
次数行列
次数行列は隣接行列と同様、行も列も頂点に対応します。頂点に接続する辺の数を表現します。そのため、対角行列になります。例のグラフの場合、次数行列$D$は次の行列で表すことができます。
実際にグラフラプラシアンを計算してみる
実際に例としたグラフでグラフラプラシアンを計算してみました。グラフラプラシアンも行と列が頂点に対応しています。グラフラプラシアンにはどの頂点が接続しているか、頂点に接続されている辺の数が情報として含まれた行列です。
$D-A$
ラプラシアンとは
グラフラプラシアンのラプラシアンは、ベクトル解析のラプラシアンに由来しています。ラプラシアンは、ラプラス作用素とも呼ばれます。作用素は、演算子のことです。記号では、$∇・∇$（$∇$はナブラ）,$∇^2$あるいは$Δ$（デルタ）で一般的に表されます。
ラプラス作用素とは、ある関数の勾配の発散をとる演算の演算子です。勾配と発散は、ベクトル解析における勾配と発散を指します。
ラプラシアンは、以下で表せます。$Δ$はラプラシアンです。$div$は発散、$grad$は勾配です。
$$Δ=div(grad)$$
グラフラプラシアンも、接続行列の転置を勾配、接続行列を発散と見立てることができます。$L$はラプラシアン行列とします。$B$は接続行列、$B^T$は接続行列の転置とします。
$$L=BB^T$$
このような理由から、ラプラシアンという名前が付きました。ちなみに、ラプラス作用素は数学者のラプラスさんからきています。ラプラスさんが研究している中で、はじめて同作用素を用いたのでラプラシアンと命名されました。
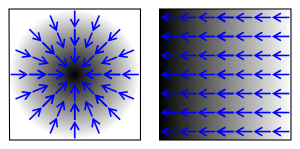
勾配のイメージ ⇒ ある座標とある座標のベクトル・スカラーの変化の量
発散のイメージ ⇒ ある座標におけるベクトルの流出量
接続行列
先程出てきた接続行列$B$と接続行列の転置$B^T$について説明します。
接続行列は、グラフにおいて頂点から出る辺は1、頂点に入る辺は-1、それ以外を0として表現します。行が頂点、列が辺に対応しています。この場合、接続行列$B$は次の行列で表すことができます。
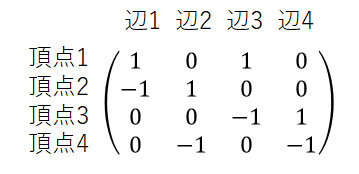
また、接続行列の転置$B^T$は次の行列で表すことができます。
ラプラシアンの説明でグラフラプラシアンは、接続行列の転置を勾配、接続行列を発散と見立てることができると書きました。では、グラフにおいて勾配と発散はどのようなイメージなのでしょうか。
グラフにおける勾配のイメージ
ある頂点とある頂点に定義された関数の差、つまり勾配として見ることができます。接続行列の転置の例だと、1行目は(1 -1 0 0)なので勾配2となります。
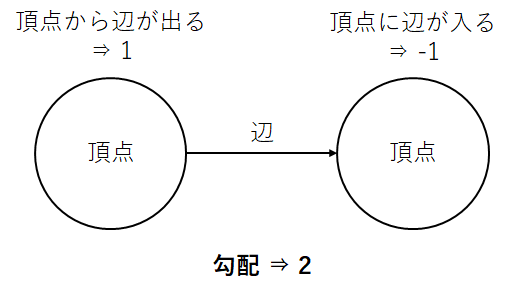
グラフにおける発散のイメージ
ある頂点に接続している辺の関数と、その頂点から他の頂点に接続している辺の関数をベクトル解析の発散と見ることができます。接続行列は、頂点から出る辺は1、頂点に入る辺は-1なので、下図の場合は、発散0となります。
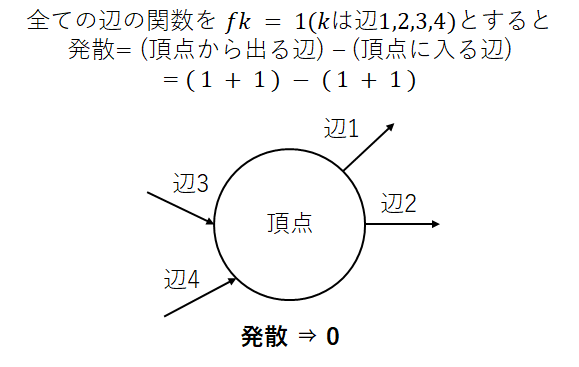
再びグラフラプラシアンを計算してみる
次は、接続行列からグラフラプラシアンを計算してみます。隣接行列と次数行列から計算した結果と同じ結果となりました。接続行列の転置を勾配、接続行列を発散と見立てて演算してもグラフラプラシアンを算出するることができたので、グラフラプラシアンとベクトル解析のラプラシアンには関係があることが見れました。
$BB^T$
まとめ
グラフラプラシアンを噛み砕いてみました。まとめると、グラフラプラシアンとは、
- グラフの構造（頂点の次数、辺のある頂点）を行列で表したもの
- グラフの性質を行列の性質に置き換えて理解できる
- 頂点に対する辺の入出力から、グラフにおける勾配と発散を表現したもの
以上です。