前回のブログでは、「Softmax関数」「交差エントロピー誤差」「Affine変換」などの逆伝播が、どのような演算処理になるかを説明し、また効率的に処理されるように設計されていることを確認しました。
今回は、その締め括りとして実際にプログラムで、逆伝播を導入することで
スピードがどのくらい改善されるのかを計測してみます。
\def\textlarge#1{%
{\rm\Large #1}
}
\def\textsmall#1{%
{\rm\scriptsize #1}
}
ニューラルネットワークのレイヤー
逆伝播のプログラムを組むにあたって、以下のような4レイヤーを考えます。
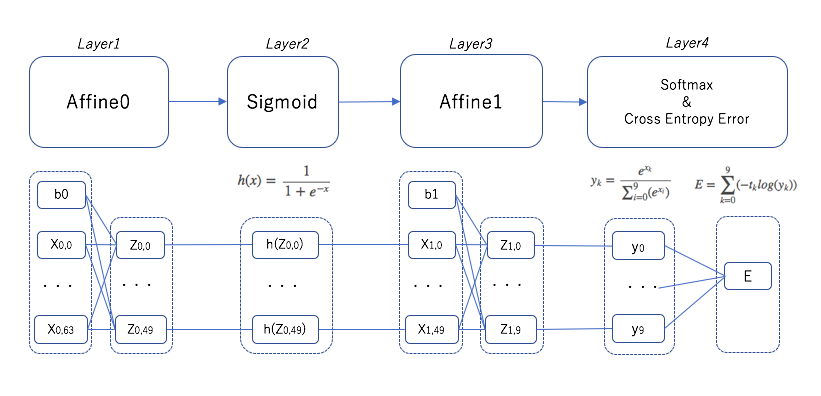
今回扱っているニューラルネットワークは2層(入力層/隠れ層)なので、Affine変換レイヤーは2つあります。
1層目と2層目の間には、活性化関数でSigmoidレイヤーがあります。
また、Softmaxと交差エントロピー誤差はまとめて扱う方が、逆伝播では都合が良いためまとめて1レイヤーで扱います。
Affine変換のレイヤークラス
Affine変換の逆伝播の演算は以下のような形です。
\frac{\partial E}{\partial X} = \frac{\partial E}{\partial Y}・W^T \\
\frac{\partial E}{\partial W} = X^T・\frac{\partial E}{\partial Y} \\
\frac{\partial E}{\partial B} = \sum_{axis=0}(\frac{\partial E}{\partial Y})
上記、逆伝播の3つめの演算である、バイアスBによる偏微分については、前回は触れていませんでしたが、∂E/∂Yのマトリックスに対して、0軸での加算する演算になります。つまり、このような演算処理です。
[[1,2,3], [100,200,300]] → [101,202,303]
PythonでのAffineレイヤーのクラスは、例えば以下のような形に書くことができます。
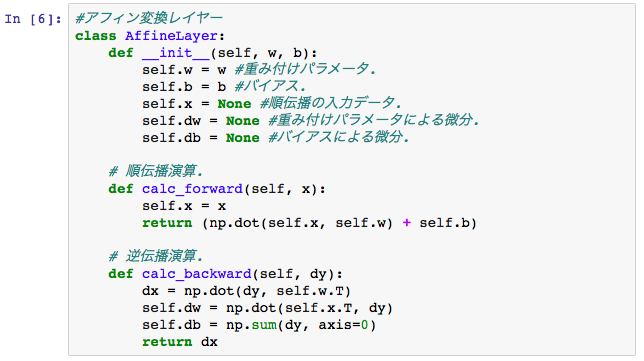
Sigmoidレイヤークラス
活性化関数のSigmoidレイヤーについては、逆伝播は以下の形でした。
\frac{\partial E}{\partial x} = y(1-y)\frac{\partial E}{\partial y}
つまり出力yについて、y(1-y)の演算結果を渡してやるだけでした。
上記のAffineレイヤーに倣って、Sigmoidレイヤーのクラスを記述すると以下のような表現になります。


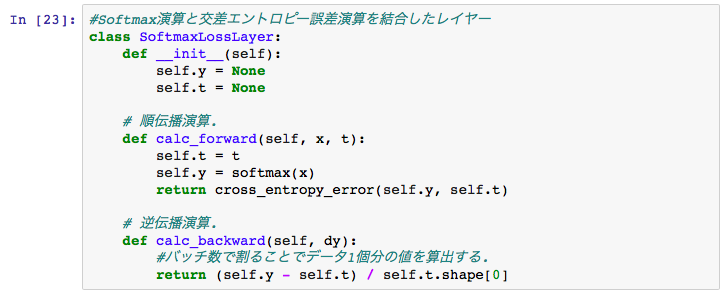
Softmaxと交差エントロピー誤差の複合レイヤー
前回のお話では、この複合レイヤーの逆伝播は、各要素について、
出力データy$\textsmall{k}$と正解データt$\textsmall{k}$の差、(y$\textsmall{k}$-t$\textsmall{k}$)を計算して渡してやるだけでした。
ニューラルネットワーククラスの拡張
このテーマの初回ブログのサンプルコードに、今回の誤差逆伝播のレイヤーを組み込んでいきます。
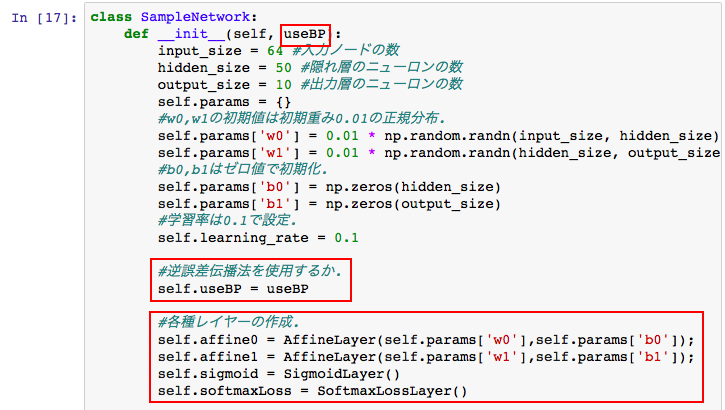
ニューラルネットワーククラス「SampleNetwork」について、まず初期化メソッド「init」を以下のように拡張します。
赤枠が変更箇所です。
今回は、誤差逆伝播法を使う場合と、使わない場合の処理速度を比較するために、「useBP」とフラグを設けています。
また、誤差逆伝播法用の4つのレイヤーを用意しています。
予測処理については、レイヤーの順伝播で行うように以下のように書き換えます。

誤差逆伝播法を用いた、勾配計算の関数として「gradient_bp」を新たに用意します。

重み付けパラメータ、バイアスパラメータの更新関数の「update_params」は、誤差逆伝播を用いる場合と、用いない場合で勾配計算を変えています。
交差エントロピー誤差の計算も、今回用意したSoftmaxLossのクラスの順伝播処理を用います。

今回、扱うデータはscikit-learnのdetasetsの文字データで変わりません。
ただ、目的変数はone-hot表現に変更しています。

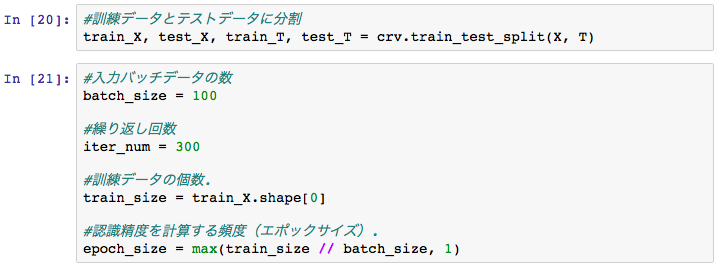
訓練データ、テストデータのスプリット、バッチのサイズ、繰り返し回数なども
前回と同じです。
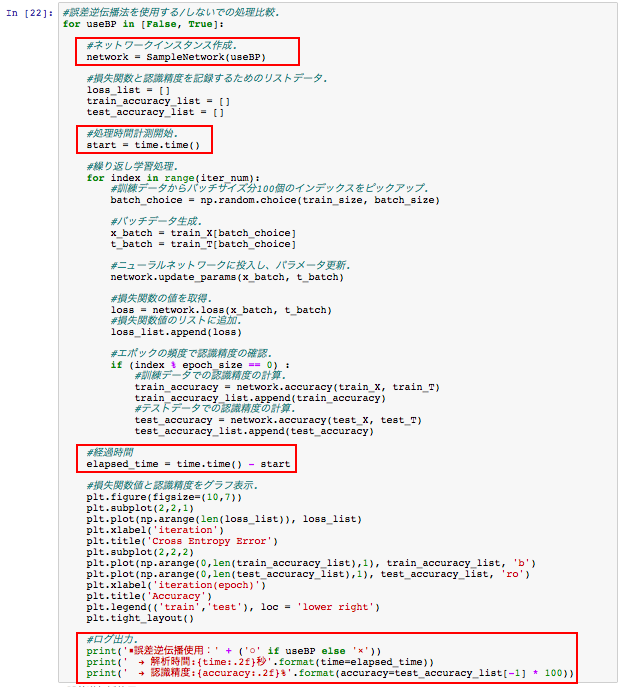
誤差逆伝播法を使用する/しないでニューラルネットワークのインスタンスを作成して、解析処理を行ってみます。
処理時間計測と、認識精度をログで出力するように処理追加しています。
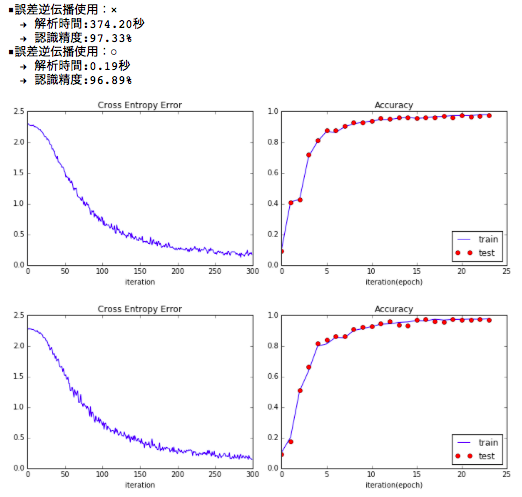
出力結果は以下のようになります。
グラフについては、上が誤差逆伝播を使用しない、下が使用したものになります。
繰り返しによる、交差エントロピー誤差の推移、認識精度の推移も近い形になっています。
誤差逆伝播法を用いた結果は、認識精度は0.44%ほど下がりはしましたが、ほぼ近い値となっています。
解析スピードについては大きな変化があります。
単純計算では (374.20秒 / 0.19秒)= 1969.47倍の速度改善が得られたことになります。
処理速度のアドバンテージは、繰り返し演算の回数を増やすことにも当てることができ、
認識精度の向上にも繋げられるメリットもあります。