はじめに
2011年にD-Waveが量子アニーリングマシンの商用販売を開始して以降、日本の大手企業も相次ぐ形で様々な(量子)アニーリングマシンの開発を開始しています。量子アニーリングマシンはイジングモデルという形式で表される最適化問題を高速に解くことが期待されています。
当社は2000年の創業当初からロジスティクス分野にいち早く着目し、ベテランさんの勘と経験に頼るしかなかった配送業務のIT化を進めてきました。巡回セールスマン問題 (Traveling Salesman Problem; TSP)はその核ともいえる問題です。NP困難という多項式時間アルゴリズムが見つかりそうにない困難な問題であり、これを量子の力を使ってスパッと解けるとすればとても嬉しいです。
先行実証
実際、既にいくつかのアニーリングマシンにおいて、TSPを解く試みは行われています。
D-Wave 2000Qと富士通デジタルアニーラについて実験を行っています。2次元平面のランダムな頂点に対しユークリッド距離を用いてTSPを解いています。変数の制約からD-Waveは8頂点、デジタルアニーラは25頂点について行っています。D-Waveについては概ね良さそうな結果が出ていますが、8頂点というのはかなり少ないです(たかだか8!=40320通りなので、古典マシンでも短い時間で総当りできます)。デジタルアニーラの25都市は交差が含まれているなど、明らかに最適解ではないものが出力されています。
東芝シミュレーテッド分岐マシンについて実験を行っています。2次元平面のランダムな頂点に対してです。距離については明言されていませんが、おそらくユークリッド距離でしょう。8頂点についてはこちらも0.2秒で最適解が得られています。10頂点も20秒かかっていますが最適解のようです。13頂点になると5分かかっても最適解が得られていません。
https://qiita.com/snhrhdt/items/d69e6b2dae5d4b439563
論文紹介です。配送計画問題 (CVPR)というTSPの拡張問題について扱っています。この中で、CVPRをクラスタリングとTSPに分けて、クラスタリングを古典マシンで、TSPをD-Waveを使って解くということを行ったようです。ここでは、頂点数が多いTSPをQBSolveというライブラリを使用して問題を分割し、D-Waveで扱えるようにしています。14,16頂点では最適解が得られていますが22頂点から近似解になり、38頂点についてはその精度も悪く、100回の実行解の偏差も大きいようです。
TSPは難しい問題とは言いましたが、流石に10数頂点レベルのものであれば古典マシンでも簡単に解くことが可能です。非量子のアニーラーの性能が悪いのは量子を使っていないせいと見ることもできるかもしれませんが、最後の論文の結果を見るかぎりでは、頂点数が多いTSPに対し、D-Waveの量子アニーラーでさえ太刀打ちできていないことが分かります。量子アニーラーで精度が得られていない38頂点のベンチマーク (Djibouti) については、古典マシンでLPソルバを使って0.24秒で解けることが知られています。
……なんだか全く量子の力でなんとかなっていないようです。これから数回の投稿にわたって、いくつかの量子アニーリングに関わる手法を比較しながら、どうしてうまくいっていないのかを考えていこうと思います。
実験
とはいえ、こちらも何も手を動かさないのもなんなので、本投稿では(低価格で)実証可能な東芝のシミュレーテッド分岐マシン (SBM) を使ってこれらの結果を追試してみることにしました。
問題条件は以下の通りです。TSPをQUBO形式に落とし込む方法についてはここで紹介すると長くなるので、また次の機会に解説しようと思います。上に挙げた記事の中でも詳しく書かれているので、そちらも参考にしてください。巡回セールスマン問題そのものについての説明も省きます。
- 2次元平面上に原点(0,0)と2次元平面[0.0,10.0]^2のランダムな頂点n-1個を置き、原点から出発してすべての頂点を通って原点に戻るTSPを解かせる。
- 距離はユークリッド距離の2乗(平方根取るのをサボりました)
- TSPの定式化は上記で挙げられているものと同じものを使用。ペナルティー関数の係数は100で固定。
- stepsは20で固定。
ランダムな頂点の設定からハミルトニアンの生成、QUBO形式への出力をC++で実装しました。単純な多項式系が実装できれば簡単に実装できる内容と思います(必ずしも多項式系を経由する必要はないかもしれません)。
SBMそのものの使い方については東芝のマニュアルを参考にしてください。クエリ送信にはInsomniaを利用しました。
http://dfk66cqpwr4ko.cloudfront.net/user_manual_en_v1_20.pdf
結果
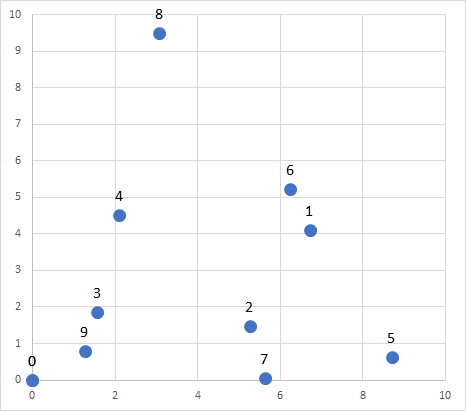
まずは、10点での実験。
頂点の座標は、
| 番号 | x座標 | y座標 |
|---|---|---|
| 1 | 6.71156 | 4.12046 |
| 2 | 5.26382 | 1.48605 |
| 3 | 1.56711 | 1.86467 |
| 4 | 2.10108 | 4.5274 |
| 5 | 8.70143 | 0.63681 |
| 6 | 6.24312 | 5.23348 |
| 7 | 5.62296 | 0.058172 |
| 8 | 3.07423 | 9.50184 |
| 9 | 1.26654 | 0.789879 |
| となりました。ここからハミルトニアンを生成し、QUBO形式に変換して東芝マシンに送ります。 |
ループ回数をいくつか変えて、以下の結果を得ました。
| 回数 | コスト | 実行時間 |
|---|---|---|
| 2500 | -1671.2474365234375 | 4.85 |
| 5000 | -1679.87841796875 | 9.70 |
| 7500 | -1678.1527099609375 | 14.99 |
| 10000 | -1684.5147705078125 | 20.00(opt) |
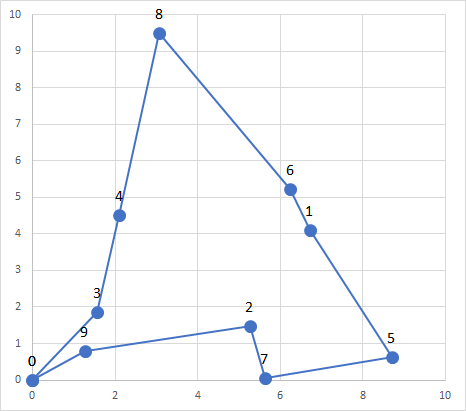
20秒、10000回のループで最適解(最短距離115.485、定数項1800)を得られました。コストについては、定数項部分を入力していないので負になっています。7500回のときより5000回のほうが良い結果が出ていて不思議ですね。
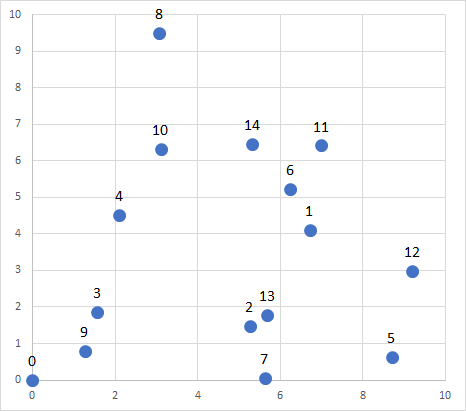
次に15頂点での実験。
頂点は先程の10点に加えて
| 番号 | x座標 | y座標 |
|---|---|---|
| 10 | 3.11353 | 6.32384 |
| 11 | 6.99359 | 6.41965 |
| 12 | 9.20024 | 2.98876 |
| 13 | 5.68746 | 1.78624 |
| 14 | 5.32574 | 6.46691 |
を追加しました。別のシード値に変えて全頂点別にしてもよかったのですが、同じシード値を流用しています。
| 回数 | コスト | 実行時間 |
|---|---|---|
| 2500 | -1724.3555908203125 | |
| 5000 | -1527.8865966796875 | |
| 7500 | -1882.862548828125 | |
| 10000 | -2242.56982421875 | |
| 12500 | -1840.1441650390625 | 25.2 |
| 20000 | -2155.900146484375 | 40.31 |
| 30000 | -1839.6444091796875 | timeout |
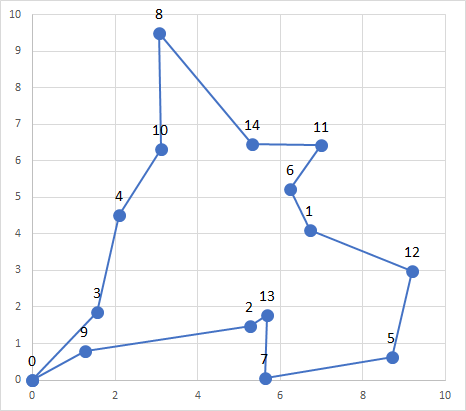
最適解は-2,706.8285(最短距離93.1715、定数項2800)です。10000回以下は実行時間メモするのを忘れましたが、明らかに最適解から遠い解なので気にしないこととします。1分でタイムアウトしたようで、20000回や30000回では最適解を得られていません。それどころか、-2200程度というスコアは制約を満たしていない解が出力されています。先程よりも顕著に実行回数とコストの関係がばらばらになっています。
ここでは特に係数などのパラメータを調整するなどしていないので、パラメータの調整である程度は改善できると思われます。東芝マシンはAWSのインスタンス代しかかかりませんが、専用マシンなどであればレンタル代はもっと高額になるので、何度もパラメータ調整しなければいけないのは実用的とは言いづらいと思います。
まとめ
- TSP(巡回セールスマン問題)を東芝のSBMを使って解いてみました。
- 10点のグラフでは20秒程度で最適解が得られました。
- 15点のグラフで既に実行可能解が得られなくなりました。
- 東芝マシンでは(今回使用したQUBOについて)実行回数を増やしてもコストが必ずしも小さくなりませんでした。
やってみたけどだめでした、という悲しい結果に終わりましたが、次回はシミュレーテッドアニーリングという量子アニーリングの元ともなった非量子のアルゴリズムを用いた場合にどうなるか、ということについて紹介していこうと思います。また、実行回数を増やしてもなぜコストが小さくならなかったのか、ということについても説明していこうと思います。
おまけ
使用した問題の最適解です。