応用情報技術者平成30年秋期 午前問76
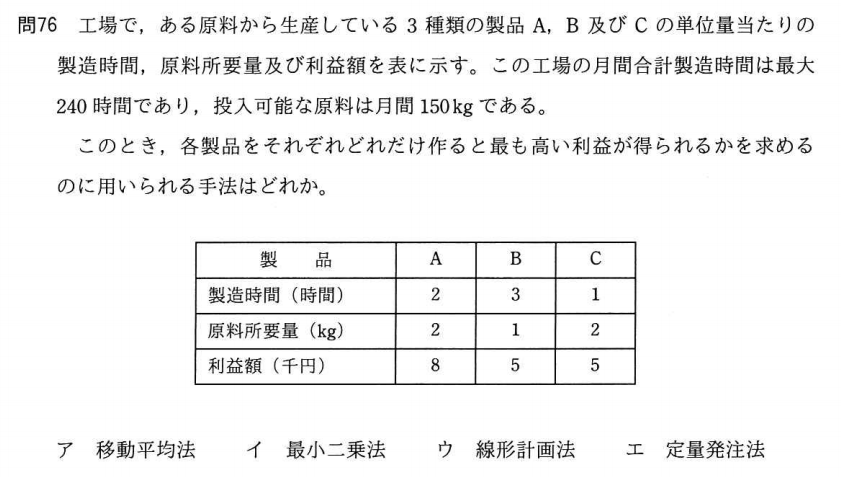
工場Xでは，ある原料から3種類の製品A，B及びCを生産している。各製品の単位量当たりの製造時間と原料所要量及び利益額は表に示すとおりである。この工場の月間合計製造時間は最大240時間であり，投入可能な原料は月間150kgである。このとき，製品A，B及びCをそれぞれどれだけ作ると最も高い利益が得られるかを知りたい。この問題を解くのに適切な手法はどれか。
１、線形計画法は、
1次式を満たす変数の値の中で式を最大化または最小化する値を求める方法です。
在庫としてもつ原材料を使用して最大の利益を得るための販売量や、機械の稼働時間を最大限に生かして製造する製品など、限りある資源を最大限に活用したい場合にその組合せを得るために用いられます。
計算方法は、下記を参照しましょう。
線形計画法超入門：
https://qiita.com/Dason08/items/e1bafb9ddc766d1c8fd0
２、移動平均法は、
時系列のデータを平滑化することで売上予測などに用いられる手法です。
例：
移動平均法は、在庫に変化があるたびに平均単価を算出して売上原価とし、棚卸資産の評価額として取り扱うための計算法です。
例えば、期首が4月1日で、以後毎月頭に仕入れを行うケースを考えてみます。
4月1日（期首）……60個、単価200円（原価12,000円）
5月1日（仕入）……40個、単価240円（原価9,600円）
6月1日（仕入）……10個、単価260円（原価2,600円）
この場合、5月1日に移動平均法による計算を行います。計算式は以下のようになります。
（5月仕入額9,600円＋在庫12,000円）÷（仕入個数40個＋在庫個数60個）＝216円
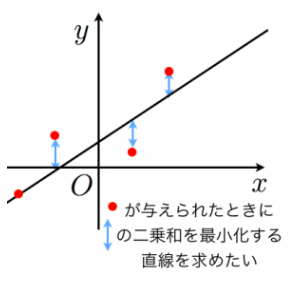
３、最小二乗法は、
散布図にプロットされた複数の点を基に数学的に回帰直線を導く方法です
例：最小二乗法（直線）の簡単な説明
最小二乗法とは，データの組 (xi,yi) が多数与えられたときに，x と y の関係を表すもっともらしい関数 y=f(x) を求める方法です。
最も基本的な例（平面における直線フィッティング）：
４、定量発注法は、
在庫を補充するための発注方式の一つです。
材料や部品を購入先に発注する場合、大きく２つの発注方式があります。
購入する材料や部品の特徴によって、発注のやり方を考える必要があります。
・定量発注方式
・定期発注方式
・定量発注方式とは、在庫量が前もって定められた水準（発注点）まで下がったとき、一定量（発注量）を発注する方式です。
・定期発注方式とは、あらかじめ、一定の期間、例えば、週に１回や月に１回のように、発注する間隔を定めておき、その都度現在の在庫量や需要量に応じて発注量を計算して発注する方式です。
参照：
https://www.fe-siken.com/kakomon/16_aki/q78.html