線形計画法超入門

#はじめに
最初に線形計画法の基本的な概念を紹介し、最後に線形計画法をPythonのライブラリPuLPで解く方法を紹介する。
理論的な概念については
「これなら分かる最適化数学 -基礎原理から計算手法まで-」(金谷健一著,共立出版)の6章「線形計画法」
PuLPについては
https://pythonhosted.org/PuLP/index.html
https://qiita.com/mzmttks/items/82ea3a51e4dbea8fbc17
を参考にした。

#線形計画とは

【Def.：線形計画】
以下の３つの特徴をもつ問題を線形計画という。

• $x_1,\cdots,x_n\in \mathbb{R}$ は全て非負
• m個の制約条件は$x_1,\cdots,x_n$の1次式による不等式(制約不等式という)
• 最大化する対象の関数$f$(目的関数)は$x_1,\cdots,x_n$の１次関数

これを数式を用いて表した標準形も記しておく。

\left\{\begin{array}{c}
a_{11}x_1+\cdots+a_{1n}x_n\leq b_1\\
\vdots\\
a_{m1}x_1+\cdots+a_{mn}x_n\leq b_m\\
\end{array}\right.\\
x_i\geq 0\quad  (^\forall i=1,2,\dots,n)\\
f = c_1x_1+\cdots+c_nx_n

この$f$を最大化する手法を**線形計画法[Linear-Programming; LP]**という。

簡単な例

何冊かの本を見ると

• 工場における生産数の最適化問題
• 最短経路問題
• 関数のfitting
  などで用いられている。ここでは、もっと一般向けに身近な内容に落とし込んで考えてみよう。

チキンカレーと親子丼を作って売る。売り上げを最大にしよう！冷蔵庫の中には

• 鶏肉50gのカタマリ：10個
• 玉ねぎ50gのカタマリ:8個
  がある。(他の具材は考えなくていいくらいたくさんあるとしよう)
  料理には

	肉のカタマリ	玉ねぎのカタマリ
カレー	1個	2個
親子丼	2個	1個

を使用する。
販売はチケット制で

	カレー	親子丼
購入に必要なチケット	2枚/皿	3枚/皿

とする。総売り上げを最大にするには、何皿ずつ作っておけばよいだろうか？

$x_1$:カレーの数、$x_2$：親子丼の数として、標準形で表してみよう。
【制約条件】

\left\{\begin{array}
xx_1 + 2x_2\leq 10\\
2x_1+x_2\leq 8\\
x_1\geq 0, x_2\geq 0
\end{array}\right.

【目的関数】

f = 2x_1+3x_2

となる。制約条件の1本目は鶏肉に関する条件式、2本目は玉ねぎに関する条件式になっている。
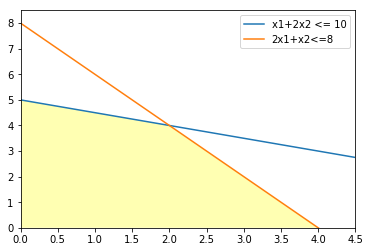
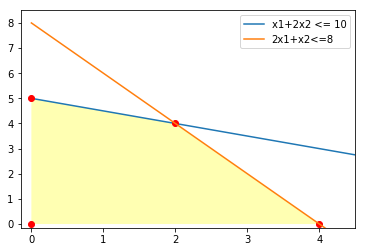
この【制約条件】を図示してみよう。

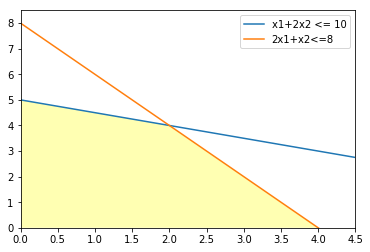
この全ての不等式を満たす点の集合(図の〜〜の部分)を許容領域、点のそれぞれを許容解という。許容解のうち、目的関数$f$を最大にする点を最適解という。

【制約条件】の不等式を等式化してみよう。今、不等式の左辺の方が右辺に比べて小さいので、その小さい分を補ってあげれば等式にすることができる。ここでは、補う分を$\lambda$として表現しよう。

\left\{\begin{array}
xx_1 + 2x_2 + \lambda_1= 10\\
2x_1+x_2+\lambda_2 =  8\\
x_1\geq 0, x_2\geq 0, \lambda_1\geq0,\lambda_2\geq0
\end{array}\right.

この$\lambda$のことをスラック変数という。例えば、先ほどの「玉ねぎに関する条件式」について考えてみよう。

2x_1+x_2+\lambda_2 = 8\\
\Leftrightarrow x_2=-2x_1+8-\lambda_2

であった。ここから、x-y平面に描いたときのy切片は$8-\lambda_2$である。

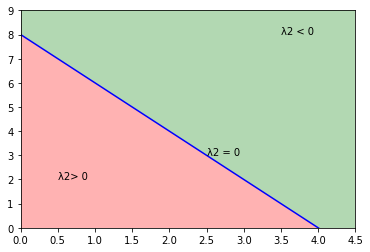
「玉ねぎに関する条件式」の等号が成立するとき、$\lambda_2 = 0$
$\lambda_2>0$のとき、等号成立時の直線より下側
$\lambda_2<0$のとき、等号成立時の直線より上側
を表現することから、$\lambda_2$の符号によって領域の分割が可能ということになる。但し、標準形を作った時に$\lambda>0$という制約を設けたことから、最適解は「直線上」or「直線より下側半分」に存在しなければならない。この「直線」を一般的に超平面といい、超平面の下側半分を$\lambda_2>0$における半空間という。

#最適解を求めるために使う定理たち

【Th.6.1】許容領域はn次元空間内の凸多面体

ここで言葉のチェックをしておこう。

【Def.：多面体】超平面(この場合直線)で囲まれた領域
【Def.：凸性】凹んでいない。

(n=2のときのイメージ)

先ほどからでてきている図であるが、確かに許容領域は直線に囲まれていて、その内部に穴がないことがわかる。

なお、証明は避けるが凸領域は単連結であるので、許容領域に穴がないことも言える。

許容領域の内部の点たち、つまり許容点のうち目的関数を最大にする点が最適解であることから、許容領域が上の性質を満たさないときは最適解を持たないと言えるだろう。改めて書くと、次のようになる。

【Lemma.:最適解が存在しないケース】
[1]許容領域が有界でなくて、目的関数が発散するとき
[2]許容領域が空集合のとき

ここでも、有界についてチェックしておこう。

【Def.:有界性を満たす集合】
半球Rの超球に含まれる集合(つまり、どの方向にもある一定の距離R以内に制限されている集合)

[1]の場合は、目的関数fは右上方向にどんどんずらしていくことができ、その結果$f\to\infty$となっていることがわかる。これでは、最適解が何であるか特定不可能である。
[2]の場合は、そもそも許容点が存在しないので最適解も存在しえない。

【Th.6.2:線形計画の基本定理】
最適解が存在するならば、目的関数は許容領域の頂点で最大値をとる。

(n=2のイメージ)

2個の超平面(直線)が交わる点(頂点)のいずれかで最適解を得る、という主張である。

ここから、n次元で頂点というのは、n個の超平面が交わる点であって、そのどこかで最適解をとる。超平面は、【制約条件】の不等式の等号が成立するときの直線であることから、次の定理が言える。

【Th.6.3】
n次元空間(多面体)における最適解 $(x_1^* ,\dots,x_n^*)$において制約条件m+n本の不等式のうちn個で等式が成立する。

ここからは、スラック変数を導入した場合の話をする。スラック変数を用いた場合の標準形は

\left\{\begin{array}{c}
a_{11}x_1+\cdots+a_{1n}x_n+\lambda_1= b_1\\
\vdots\\
a_{m1}x_1+\cdots+a_{mn}x_n+\lambda_m= b_m\\
\end{array}\right.\\
x_i\geq 0,\lambda_j\geq 0\quad  (^\forall i=1,2,\dots,n,^\forall j=1,2,\dots,m)\\
f = c_1x_1+\cdots+c_nx_n

である。このとき、【Th.6.3】は次のように書き換えることができる。

【Th.6.4】
スラック変数導入後の最適解において、n+m個の値$x_1^* ,\cdots ,x_n^* $,$ \lambda_1^* ,\cdots,\lambda_m^* $のうちn個は0になる。

$^\exists i\in [1,n]$で$x_i=0$ならば、座標軸が最適解を与える頂点をなす直線のうちの１つのとき
$^\exists j\in [1,m]$で$\lambda_j=0$ならば、座標軸以外の直線(【制約条件】の等号成立をさせた直線)が最適解を与える頂点をなす直線のうちの１つとなったときである。
#最適解を求めにかかる
以上の定理たちを使って、自然に考えられる解法は次の方法であろう。

【Method.1】
[1]【制約条件】のm+n個の不等式からn個を選んで等号に置換した連立1次方程式を解く。
[2]『解が非負』『【制約条件】への妥当性』をCheck
[3][2]がOKならば、$f$の値を計算
[4][1]~[3]を全ての場合についてやる。その結果得られる$f$の値が最大となるものを選ぶ。

スラック変数を導入した場合は次のようになる。

【Method.2】
[1]n+m個の変数$x_i,\lambda_j$からn個を選んで0とおく。その結果得られる連立1次方程式を残ったm個の変数について解く。
[2]『解が非負』をCheck
[3][2]がOKならば、$f$の値を計算
[4][1]~[3]を全ての場合についてやる。その結果得られる$f$の値が最大となるものを選ぶ。

いずれの場合も[1]で選ぶ通り数が $_{m+n}C_n$ 通りとなり、mやnが増えて複雑な条件になると一気にコストが急増してしまうところに欠点がある。コストがかかるという欠点を改善する方法の一つとして「シンプレックス法」などがある。

#PuLPで解く
今回は、冒頭紹介したカレーと親子丼の最適化問題を解くことにしよう。もう一度問題を整理しておく。
$x_1$:カレーの数、$x_2$：親子丼の数に対して
【制約条件】

\left\{\begin{array}
xx_1 + 2x_2\leq 10\\
2x_1+x_2\leq 8\\
x_1\geq 0, x_2\geq 0
\end{array}\right.

【目的関数】

f = 2x_1+3x_2

で、この$f$を最大化しようというものであった。
まずは、Pythonのコードを全文載せる。

import pulp

#線形計画の定義
problem = pulp.LpProblem('Curry_Oyako', pulp.LpMaximize)

#変数の定義
Curry = pulp.LpVariable('Curry', 0, 10, 'Integer') 
Oyako = pulp.LpVariable('Oyako', 0, 10, 'Integer') 

#目的関数の定義
problem += 2*Curry + 3*Oyako

#制約条件の定義
problem += Curry + 2*Oyako <= 10
problem += 2*Curry + Oyako <= 8

#解く
status = problem.solve()
print(pulp.LpStatus[status])

#結果表示
print("Result")
print("Curry:",Curry.value())
print("Oyako:",Oyako.value())

まずは、問題を定義しよう。

problem = pulp.LpProblem('Curry_Oyako', pulp.LpMaximize)

ここでは、線形計画問題に名前を「Curry_Oyako」とつけ、最終的な目標は目的関数$f$を最大化することであるので「pulp.LpMaximize」と指定した。(最小化したいときはpulp.LpMiniimize)とする。

次に変数の定義をする。今回はカレーと親子丼の皿数を変数としたので、それらを定義する。なお、小数点の皿数が出ても調理に困るので整数枚となるようにIntegerを指定する(他にはfloat型連続値'Continuous'、2値変数'Binary'が指定できる)。また、変数の最小値、最大値はそれぞれ0,10で指定した。

Curry = pulp.LpVariable('Curry', 0,10,  'Integer') 
Oyako = pulp.LpVariable('Oyako', 0, 10,'Integer') 

さて、変数定義まで終わったら制約条件と目的関数を定義しよう。設定は本当に楽。なんと線形計画問題problemに足すだけ。最高。

problem += Curry + 2*Oyako <= 10
problem += 2*Curry + Oyako <= 8

problem += 2*Curry + 3*Oyako

以上で定義はおしまい。定義がうまくいっているか確かめたい場合は、全ての定義を終了したあとに

print(problem)

とすれば出力は

Curry_Oyako:
MAXIMIZE
2*Curry + 3*Oyako + 0
SUBJECT TO
_C1: Curry + 2 Oyako <= 10

_C2: 2 Curry + Oyako <= 8

VARIABLES
0 <= Curry <= 10 Integer
0 <= Oyako <= 10 Integer

となり、確認することができる。
あとは、解いてもらおう。解くのも一瞬。

status = problem.solve()
print(pulp.LpStatus[status])

解くことの本質はproblem.solve()だけである。これが正確に実行されたかどうかをチェックするためにstatusを表示している。これが"Optimal"と表示されれば、ちゃんと解けたということになる。では、結果を見よう。変数に対して".value()"とするだけである。

print("Result")
print("Curry:",Curry.value())
print("Oyako:",Oyako.value())

Result
Curry: 2.0
Oyako: 4.0

図的にも(2,4)な気はしていたが、その通り！
PuLP本当に楽で直感的でよさげですね！
#さいごに
この記事は自主ゼミの発表で取り上げた内容をもとに、厳密的な話は置いておいて線形計画法の直感的な理解とPythonで解く演習を兼ねたものであった。特にPuLPはプログラミングをほぼ知らない人でも使えそうなツールで、とにかく楽そうであった。また、高校数学でよく見る線形計画法が実際の問題として取り扱われていることも実感できてよかった。
#Appendix(領域を塗る)
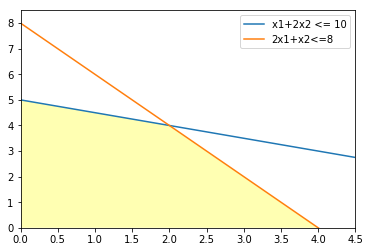
本文中の図の描き方をまとめておく。本記事の趣旨とは全く異なるが、自分自身の備忘録的な何かも込めてまとめる。使用したのは、matplotlibとnumpyである。

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(0, 5, 100)

y1 = 5 - 0.5*x
y2 =  8 - 2*x
y3 = np.zeros_like(x)

y4 = np.minimum(y1, y2)

plt.figure()
plt.plot(x, y1, label="x1+2x2 <= 10")
plt.plot(x, y2, label="2x1+x2<=8")
plt.fill_between(x, y3, y4, where=y4>y3, facecolor='yellow', alpha=0.3)
plt.ylim(0, 8.5)
plt.xlim(0, 4.5)
plt.legend(loc=0)

plt.show()

x軸の区間[0,5]を100分割して、その値について定義したy1,y2,y3を計算し、それをプロットしたというものである。

y3 = np.zeros_like(x)

は、0を要素とする配列を返す関数。

plt.fill_between(x, y3, y4, where=y4>y3, facecolor='yellow', alpha=0.3)

は、「y3、つまりy=0」と「各xについてy1とy2の小さい方y4」について、$y_4>y_3=0$を黄色で塗る。alphaは不透明度を指定する。
これを実行して得られる図は

である。