はじめまして @lxacas です.
前日の @Sz_Show 氏の楕円曲線暗号の記事タイトルに触発され,私も暗号系の記事を書かねばと思い参加しました.
本記事も楕円曲線暗号について扱いますが,暗号そのものの実装はおこないません.
本記事では,
- ECDH や ECDSA などの暗号技術を支える楕円曲線の性質について説明します.
- 楕円曲線上の演算を利用する ECDH 鍵交換アルゴリズムについて解説・実装を試みます.
やっていきましょう.
Elliptic Curve
数学が不得手&理解不足なので図をたっぷり使います.
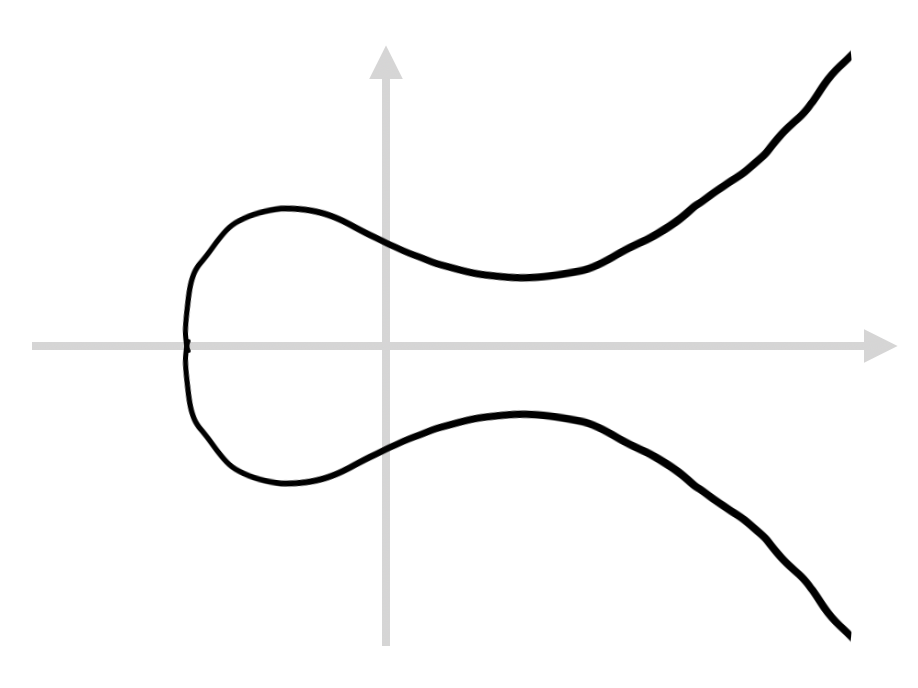
楕円曲線は,表現系式がいくつかありますが,私が調べた範囲では以下のワイエルシュトラス標準形で与えられることが多いです.
\mathbb{E}:y^2 = x^3+ax+b~~~~~~~~~~(1)
式(1)は座標軸の取り方によって変形が可能で,射影座標型,モンゴメリ型などがあるようです.
楕円曲線暗号でよく使われる性質として,曲線上の 点同士の加算 があります.
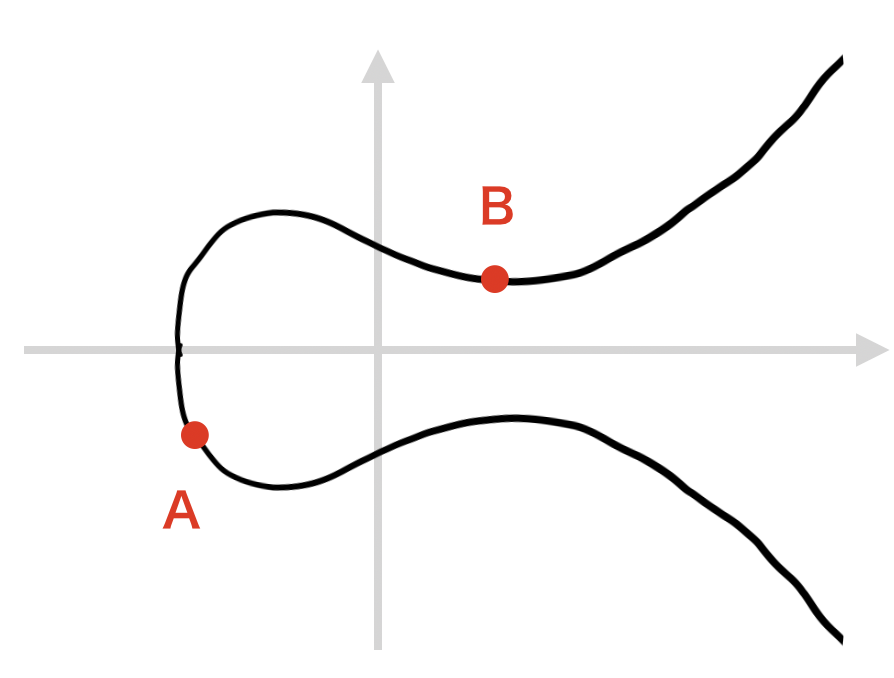
楕円曲線$\mathbb{E}$上の点をA, B を選んで直線を引くと,式(1)右辺が三次方程式であることから,3つ目の交点が見つかります.
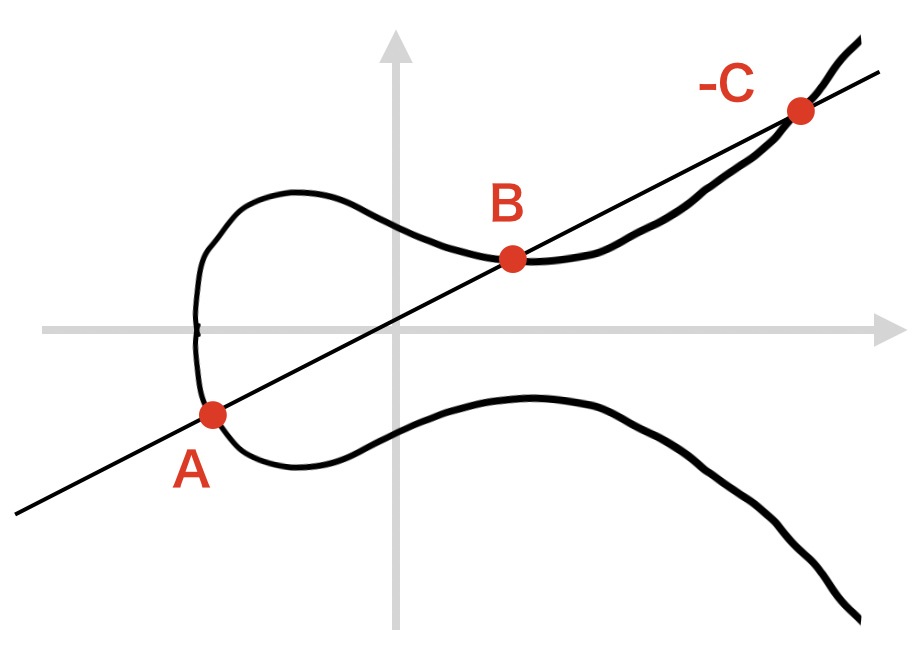
3つ目の交点を -C と定義します.式(1)を変形すると,
y=\pm \sqrt{x^3+ax+b}
となることから,楕円曲線上のある x 座標に対し,y が2通りの値を取りうることが分かります.
-C のX軸に関して対称な点を C とします.
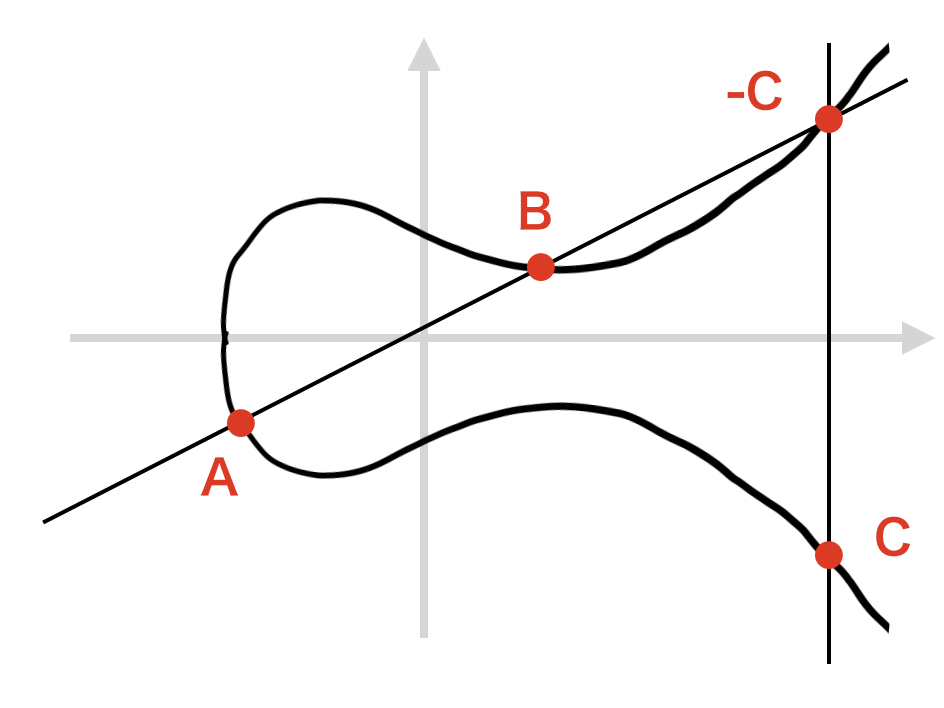
以上の処理を C = A + B となるような楕円曲線 $\mathbb{E}$ 上の加算として考えると,
無限遠点$\mathcal{O}$を単位元としたとき,楕円曲線 $\mathbb{E}$ 上の点の集合は,加法群となります.
さらに,説明は省略しますが,$\mathbb{E}$ 上の点の2倍算も可能です.
2倍算と加算ができると,点の整数倍を多項式時間で求めることができます.
例:11Aの計算
11A=10A+A=2*5A+A=2*(4A+A)+A=2*(2*2A+A)+A=2*(2*2*A+A)+A
2倍算が3回,加算が2回で求められ,単純に11回加算をするより高速です.
さいごに,楕円曲線の演算は,有限体上でも定義することが可能です.
このとき$x,~y$の関係式は,素数 $p$ を法とする有限体上で
\mathbb{E(F}_p):y^2 = x^3+ax+b~~\text{mod}~~p
と表されます.
デジタルの世界では限られた整数空間だけ用いられれば良いため,
無限に加算ができてしまう式(1)よりも都合が良いのです.
これで実装の準備が整いました.
実装
楕円曲線クラスを実装しました.
楕円曲線上の点同士の加減算,楕円曲線上の点に対する2倍算やスカラー倍算が計算できます.
※ソースコードが長いのでご注意ください
% Define an elliptic curve and operations
classdef EllipticCurve < matlab.mixin.SetGetExactNames
%% Elliptic Curve Parameters
properties %(Constant)
% 24 bit Elliptic Curve
% y^2 = x^3 + ax + b mod p
CoefA = 9733481 %Coefficient a
CoefB = 3868448 %Coefficient b
Prime = 16777199 %Prime number p
BaseG = struct('X',10641273,'Y',10020383) %Base pont G
Order = 16769017 %Order of Elliptic Curve
end
%% Functions
methods
%% Modular Functions on Finite Field
% Modular Inverse on finite field
% d = x^-1 mod Prime
function d=InvFF(obj,x)
% extended euclidean algorithm
r0=x;r1=obj.Prime;
x0=1;x1=0;
y0=0;y1=1;
while r1>0
q=floor(r0/r1);
r2 = mod(r0,r1);
x2 = x0 - q*x1;
y2 = y0 - q*y1;
r0 = r1; r1 = r2;
x0 = x1; x1 = x2;
y0 = y1; y1 = y2;
end
d=x0;
end
%% Elliptic Curve Functions
% Doubling point on elliptic curve
% 2U = 2 * U
function doubleU=double_E(obj,U)
if U.Y==0
doubleU.X=0;doubleU.Y=0;
return
end
lamda=mod(mod(3*mod(U.X^2,obj.Prime),obj.Prime)+obj.CoefA,obj.Prime);
lamda=mod(lamda*InvFF(obj,mod(2*U.Y,obj.Prime)),obj.Prime);
doubleU.X=mod(mod(lamda^2,obj.Prime)-mod(2*U.X,obj.Prime),obj.Prime);
doubleU.Y=mod(mod(mod(U.X-doubleU.X,obj.Prime)*lamda,obj.Prime)-U.Y,obj.Prime);
end
% Addition points on elliptic curve
% U + V = W
function W=add_E(obj,U,V)
if U.X==V.X
if U.Y==obj.Prime-V.Y
W.X=0;W.Y=0;%decide (0,0) as infenity point
return
elseif U.Y==V.Y
W=double_E(obj,U);
return
end
end
if U.X==0&&U.Y==0
W.X=V.X;W.Y=V.Y;%if input infenity point, return another input
return
elseif V.X==0&&V.Y==0
W.X=U.X;W.Y=U.Y;
return
end
lamda=mod(mod(V.Y-U.Y,obj.Prime)*InvFF(obj,mod(V.X-U.X,obj.Prime)),obj.Prime);
W.X=mod(mod(mod(lamda^2,obj.Prime)-U.X,obj.Prime)-V.X,obj.Prime);
W.Y=mod(mod(mod(U.X-W.X,obj.Prime)*lamda,obj.Prime)-U.Y,obj.Prime);
return
end
% Substract points on elliptic curve
% W = U - V
function W=sub_E(obj,U,V)
V.Y=mod(-V.Y,obj.Prime);
W=add_E(obj,U,V);
return
end
% Scalar multiplication of points on elliptic curve
% kU = k * U
function kU=scalar_times_E(obj,U,k)
% set infinity point
kU=struct('X',0,'Y',0);
%Binary method
for i=ceil(log2(k)):-1:1
kU=double_E(obj,kU);
if bitget(k,i)==1
kU=add_E(obj,kU,U);
end
end
end
%% Graph
% Plot elliptic curve and input point.
function plot_EC(obj,varargin)
if nargin==2
% Plot a point A
Xp=varargin{1};
Yp=sqrt(Xp^3+obj.CoefA*Xp+obj.CoefB);
plot(Xp,Yp,'o')
hold on
end
if nargin==3
% Plot point's A, B, C, D
% D = A + B, C = -D on elliptic curve
Xp(1)=varargin{1};
Yp(1)=sqrt(Xp(1)^3+obj.CoefA*Xp(1)+obj.CoefB);
Xp(2)=varargin{2};
Yp(2)=sqrt(Xp(2)^3+obj.CoefA*Xp(2)+obj.CoefB);
plot(Xp(1),Yp(1),'o',Xp(2),Yp(2),'o');hold on
Inc=(Yp(2)-Yp(1))/(Xp(2)-Xp(1));
Int=Yp(1)-Inc*Xp(1);
Xp(3)=max(roots([1 -(Inc^2) obj.CoefA-2*Inc*Int obj.CoefB-(Int^2)]));
Yp(3)=sqrt(Xp(3)^3+obj.CoefA*Xp(3)+obj.CoefB);
Xp(4)=Xp(3);Yp(4)=-Yp(3);
plot([min(Xp(1:2)),Xp(3)],[min(Yp(1:2)),Yp(3)])
plot([Xp(3) Xp(4)],[Yp(3) Yp(4)],'-o')
end
% Set plot parameter
Scale=10;Resol=1000;
if nargin>1
Scale=max(Xp)*2;
end
% Find root of elliptic curve. x^3 + ax + b = 0
Root=roots([1 0 obj.CoefA obj.CoefB]);
% Find intersection with y axis
XrangeMin=Root(angle(Root)==pi);XrangeMax=Scale+XrangeMin;
X=[XrangeMax:-(Scale/Resol):XrangeMin XrangeMin:(Scale/Resol):XrangeMax];
Y=zeros(1,length(X));
Y(1:length(X)/2)=-sqrt(X(1:length(X)/2).^3+obj.CoefA*X(1:length(X)/2)+obj.CoefB);
Y(length(X)/2+1:end)=sqrt(X(length(X)/2+1:end).^3+obj.CoefA*X(length(X)/2+1:end)+obj.CoefB);
plot(X,Y,[-2*Scale/10 Scale],[0 0],'--');
end
end
end
このクラスは,お試しでプロットメソッドを実装しています.
プロットの実装方法に自信のない箇所1がいくつかありますが,是非遊んでみてください.
使用例1
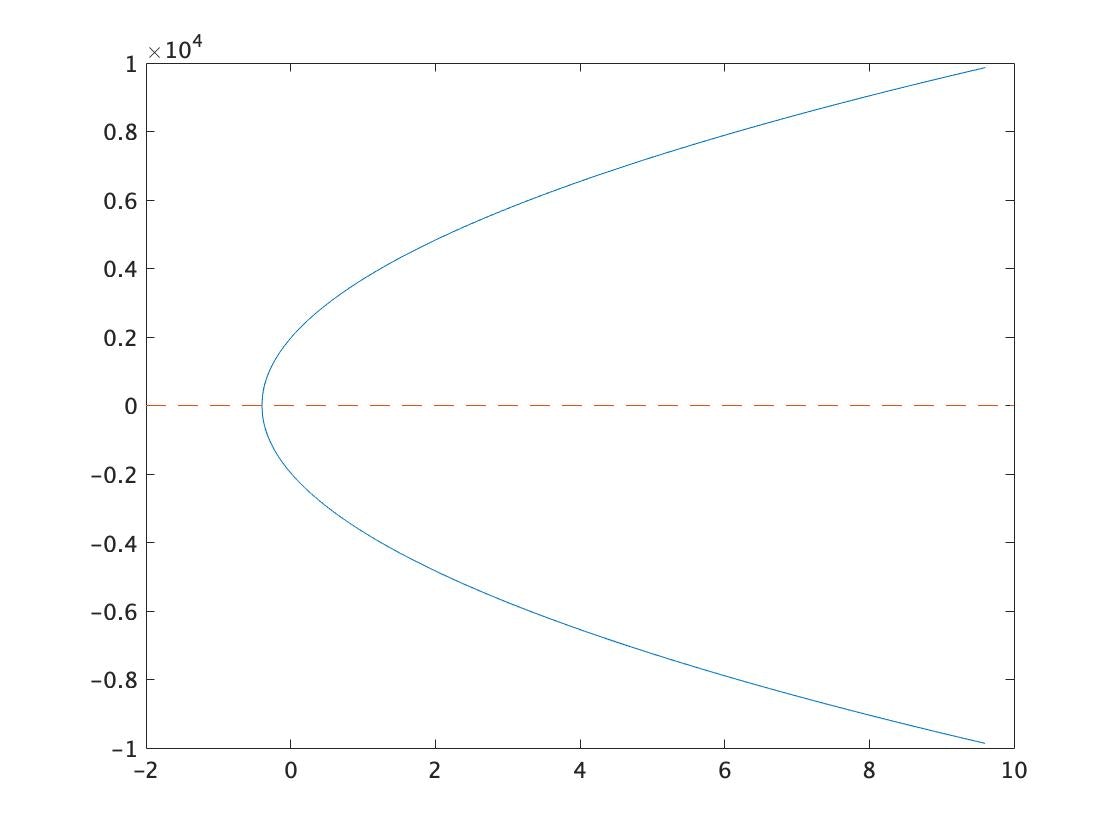
Alice の楕円曲線インスタンスを生成し,表示します.
>> Alice=EllipticCurve;
>> Alice.plot_EC()
出力
使用例2
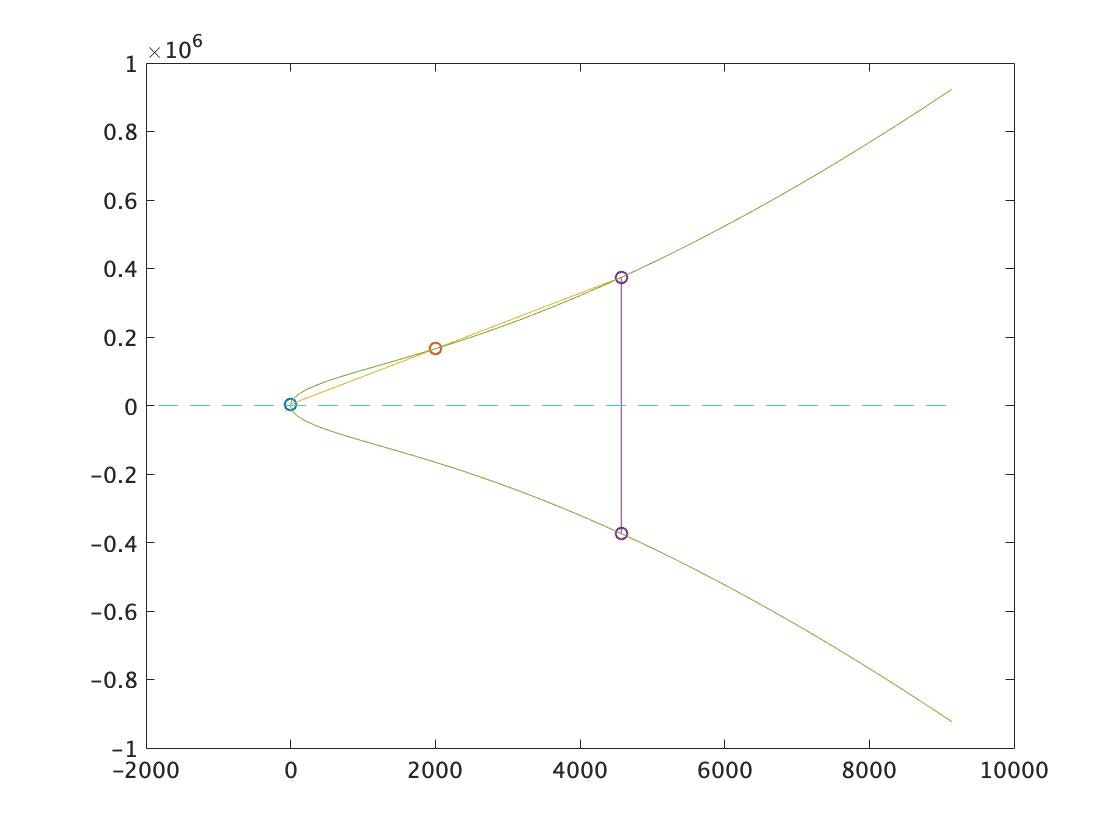
楕円曲線上に点X1, X2 をプロットさせます.
さらに,X3=X1+X2 を求めて表示します.
>> X1=1;X2=2000;
>> Alice.plot_EC(X1,X2)
出力
ECDH
ECDH は,Diffie-Hellman 鍵共有アルゴリズムを有限体上の楕円曲線で実現するアルゴリズムです.
インターネットを介した通信は便利ですが,通信経路を制限することが難しいため,送信者が意図しない相手にも伝わってしまう恐れがあります.
そこで暗号技術によって秘匿化することで,通信の傍受を防ぐことができます.
しかし,AES をはじめとする多くの共通鍵暗号方式は,事前に通信相手と秘密鍵を共有しなければなりません.
このとき,鍵を共有していない(=暗号通信できない)離れた相手と安全に鍵共有をおこなう方法の一つとして, ECDH があります.
原理
楕円曲線上のある1つの点 $G$ をベースポイントとします.
$\mathbb{E(F}_p)$は加法群のため,$G$ に自分自身を足し続ければ,いずれ無限遠点 $\mathcal{O}$ に到達し,もう一度 $G$ を足すと自分自身に戻ります.( $\mathcal{O}$ は単位元のため)
このとき,
\mathcal{O}=nG
となるような整数 $n$ を $\mathbb{E(F}_p)$ の位数と呼びます.
ここで,以下のような関係式を満たす点Aから整数 $ka$ を求める問題を楕円曲線上の離散対数問題といい,困難であることが知られています.
A=kaG,~~\{ka\in\mathbb{Z}~|~ka<n\}
直感的には,$G$ を1回ずつ足し合わせて確認すれば良いように思われますが,位数 $n$ が巨大な場合,その計算量は現実的でないため困難です.
また,楕円曲線上の点同士の除算は成立しないため,点 $A$ を点 $G$ で割ることもできないのです.
ECDH は,離散対数問題が困難であることを利用し,秘匿されていない通信路上での鍵交換を実現します.
Alice と Bob がこれから暗号通信をするため,秘密鍵を共有したいとします.
ECDHは3つのステップ2で構成されます.
1. 最初のステップは,お互いに1以上 $n$ 未満の秘密の数字 $ka,kb$ を生成し,ベースポイント $G$ にかけます.
A=kaG,~~~B=kbG
2. 次に,Alice は点 $A$ を,Bob は点 $B$ を相手に送ります.
3. 最後に,Alice と Bob は,受け取った点に対し,自分の秘密の数字をかけます.
S=kbA=kaB=kakbG
通信路上には $ka$ も $kb$ も流れないため,二人は安全に秘密鍵 $S$ を作ることができます.
実装
ECDH クラスを実装しました.先ほど掲載した EllipticCurve クラスを継承しています.
※またまたソースコードが長いのでご注意ください
classdef ECDH < EllipticCurve
%% Elliptic Curve Diffie-Hellman key exchange class
properties (Access = protected)
% These variable are your secret information
ShareKey %Shared Secret Key
SecNum %Secret Number
CAES %Class of AES
end
% Const numbers
properties (Constant)
NORBYT=3 %Normalize message to multiples of 3 Byte.
BYTE=8 %1 Byte = 8bit
FILE_IS_EXIST=7 %exist(dir)==7
end
%% Functions
methods
function obj=ECDH()
% Generate your secret number
obj.SecNum = randi(obj.Order);
end
% Send your random number by elliptic curve point
function rG=SendP(DH)
% rG = SecNum * BaseG
% hide your random number in a point of elliptic curve
rG=DH.scalar_times_E(DH.BaseG,DH.SecNum);
end
% Receive another one's random number and
% caliculate shared secret key
function RecvP(DH,rG)
% SecKey = Alice's randnum * Bob's randnum * Base Point G
% Set SharedKey to class properties
DH.set('ShareKey',DH.scalar_times_E(rG,DH.SecNum));
% If you download ↓ "AES project" ↓, ECDH class uses it.
% https://jp.mathworks.com/matlabcentral/fileexchange/
% 73037-matlab-aes-encryption-decryption-example
if exist('AES','dir')==7
addpath AES
DH.set('CAES',AES(DH.ShareKey.Y,'SHA-1'));
end
end
% Encrypt message by shared secret key and Send Cipher Text
function CipherTxt=SecureSend(DH,Message)
% check input text data type.
assert(isa(Message,'char'),'Please input char type.')
% Encrypt Message by AES algorithm
if exist('AES','dir')==DH.FILE_IS_EXIST
CipherTxt=DH.CAES.encrypt(Message);
% Encrypt Message by XOR, it is cheap trick.
else
CipherTxt=DH.XOREncrypt(Message);
end
end
% Receive an encrypted message and decrypt it
function DecMessage=SecureRecv(DH,CipherTxt)
% Decrypt Message by AES
if exist('AES','dir')==DH.FILE_IS_EXIST
DecMessage=DH.CAES.decrypt(CipherTxt);
% Decrypt Message by XOR
else
DecMessage=DH.XORDecrypt(CipherTxt);
end
end
% XOR Encryption
function CipherTxt=XOREncrypt(DH,Message)
MsgLen=strlength(Message);
% Normalize to multiples of 3 Byte
MsgLen=MsgLen+(DH.NORBYT-rem(MsgLen,DH.NORBYT));
CipTmp=zeros(1,MsgLen,'uint32');
CipTmp(1:length(Message))=Message;
CipherTxt=zeros(1,MsgLen/DH.NORBYT,'uint32');
for i=1:MsgLen/DH.NORBYT
% encode
for j=1:DH.NORBYT
CipherTxt(i)=CipherTxt(i)+bitshift(CipTmp((i-1)*DH.NORBYT+j),...
DH.BYTE*(DH.NORBYT-j));
end
% Encryption
CipherTxt(i)=bitxor(CipherTxt(i),DH.ShareKey.Y);
end
end
% XOR Decryption
function DecMessage=XORDecrypt(DH,CipherTxt)
MsgLen=length(CipherTxt);
DecTmp=char(zeros(1,MsgLen*DH.NORBYT,'uint8'));
for i=1:MsgLen
% Decryption
CipherTxt(i)=bitxor(CipherTxt(i),DH.ShareKey.Y);
% decode
for j=1:DH.NORBYT
DecTmp((i-1)*DH.NORBYT+j)=bitand(bitshift(CipherTxt(i),...
-DH.BYTE*(DH.NORBYT-j)),255);
end
end
DecMessage=char(DecTmp);
end
end
end
使用例1:鍵交換
秘密の通信をしたい Alice と Bob を生成します.
>> Alice=ECDH;Bob=ECDH;
二人とも生成時に秘密の数字 $ka,kb$を所有します.
ECDH クラスの property を public に変更して覗いてみると,
>> Alice.get('SecNum')
ans =
1635657
となります.
Alice は,秘密の数字 1635657 を楕円曲線上の点 $A\in\mathbb{E(F}_p)$ に隠したまま Bob に送ることができます.
>> A=Alice.SendP
A =
フィールドをもつ struct:
X: 6979220
Y: 1604013
>> Bob.RecvP(A)
$A$ に隠された $ka$ を求めるのは困難なため,$A$ を Bob 以外の誰かに見られても構いません2.
Bob は Alice から受け取った $A$ に,自分だけが知っている $kb$ をかけて共有鍵 $S$ を手に入れることができます.
>> Bob.get('ShareKey')
ans =
フィールドをもつ struct:
X: 2324117
Y: 12856075
Alice も Bob に点 $B$ を送ってもらうことで,全く同じ鍵を手に入れることができます.
>> Alice.RecvP(Bob.SendP)
>> Alice.get('ShareKey')
ans =
フィールドをもつ struct:
X: 2324117
Y: 12856075
これで暗号通信の準備が整いました.
使用例2:暗号化通信
せっかく秘密鍵を共有したのに暗号通信をしないのは寂しいので,暗号/復号インターフェースを用意しました.
インターフェースからAESライブラリを参照し,ECDH クラスで共有した鍵を用いて暗号・復号をおこないます.(ダウンロードはご自身の責任でお願いいたします)
>> CipherTxt=Alice.SecureSend('Sorry for being late for the deadline on December 16th.')
CipherTxt =
"QJrl6FxfI+b6YuW2QiS3Rx5YJtBtnTgq9wvEJjyh6EUNxl44oDyklXwZ19iTn2bYPNy0TbHj/wzfQfM1/Y0+vA=="
>> Bob.SecureRecv(CipherTxt)
ans =
"Sorry for being late for the deadline on December 16th."
また,AESライブラリとは別に,メッセージと共有鍵の bit ごとの xor を取るだけの,とてもシンプルな暗号機能も実装しました.AESライブラリが無い環境ではこちらが呼ばれます.
>> CipherTxt=Alice.SecureSend('Please click good button')
CipherTxt =
1×9 の uint32 行ベクトル
9717614 10836078 14960743 11356256 14961764 11226923 10903167 11551845 12856075
>> Bob.SecureRecv(CipherTxt)
ans =
'Please click good button '
おまけ:鍵の漏洩
私の実装した XOR 暗号は,空文字を入れると秘密鍵がそのまま出てくるという致命的な脆弱性があります.
大事な通信には使わないでください.
>> CipherTxt=Alice.SecureSend('')
CipherTxt =
uint32
12856075
>> Alice.get('ShareKey')
ans =
フィールドをもつ struct:
X: 2324117
Y: 12856075
おわりに
担当日に投稿できず申し訳ありませんでした.
コードを書くのはとても楽しかったし,MATLABの便利な機能を沢山知ることができて良かったです.
本当はECDSAも紹介したかったのですが,時間の制約と予想以上に文量が増えてしまったため次の機会にしたいと思います.
参考文献
この記事は以下の情報を参考にして執筆しました。
- 「暗号技術のすべて」IPUSIRON,翔泳社
- 「暗号理論と楕円曲線」辻井重男ほか,森北出版