引き続きLorenz96モデルを使ってデータ同化をしていきます.今回はEnsemble Kalman Filterの解説記事です.データ同化の基礎の記事やExtended Kalman Filterの記事の内容は既知のものとして扱うので,わからない用語があったときはそちらを参照してください.
Julia言語Ver1.3.1を用いています.
追記(2020/7/28):EnSRFのアルゴリズムで$\tilde{K}$が間違っていたので訂正。機会があればちゃんと導出まで書きます。
Ensemble Kalman Filter
Ensemble Kalman Filter (EnKF)はその名の通りサンプルをとってアンサンブル平均で計算をする手法です.1994年の登場以来様々な改良が重ねられています.この記事では,もっとも基礎的なPO法とSRFを紹介します.文献として創始者Geir Evensenによる"The Ensemble Kalman Filter: theoretical formulation and practical implementation"を挙げておきます.
EnKF(?)
一番最初にGeir Evensenによって"Sequential data assimilation with a nonlinear quasi‐geostrophic model using Monte Carlo methods to forecast error statistics"で提唱されたものを説明します.
$m$個のサンプル$x^{f,k},x^{a,k}(1\leq k\leq m)$を用いてKalman Filterの共分散行列$P^f$の式をアンサンブル平均で書き換えます.$\bar{x}^a,\bar{x}^f$をそれぞれ$x^{a,k},x^{f,k}$の平均とします.
アルゴリズム
Forecast Step
\begin{align}
x^{f,k} &= M(x^{a,k})\\
\delta X^f &= \left(x^{f,1}-\bar{x}^f, \ldots , x^{f,m} - \bar{x}^f \right) \\
P^f &= \frac{1}{m-1} \delta X^f (\delta X^f)^{\top}
\end{align}
Analysis Step
\begin{align}
K &= P^f H^{\top}(HP^f H^{\top} + R)^{-1}\\
x^{a,k} &= x^{f,k} + K(y - Hx^{f,k})
\end{align}
ポイントはサンプル計算によって$M$の導関数を計算する必要がなくなっていること,$P^a$の計算が必要なくなっていることです.非常に大きな利点です.
実装と解説
先に全体のプログラムを示してから解説します.サンプル数memberを200として上記のアルゴリズムに従って計算し,L96_EnKF_output.txtに結果を出力するプログラムです.
using LinearAlgebra
using Statistics
using Random
using DelimitedFiles
## L96modelの右辺
function L96(u; F = 8.0, N = 40)
f = fill(0.0, N)
for k = 3:N-1
f[k] = (u[k+1] - u[k-2]) * u[k-1] - u[k] + F
end
f[1] = (u[2] - u[N-1]) * u[N] - u[1] + F
f[2] = (u[3] - u[N]) * u[1] - u[2] + F
f[N] = (u[1] - u[N-2]) * u[N-1] - u[N] + F
return f
end
# 4-4Runge-Kutta
function Model(u; dt = 0.05)
du = u
s1 = L96(u)
s2 = L96(u + s1 * dt / 2)
s3 = L96(u + s2 * dt / 2)
s4 = L96(u + s3 * dt)
du += (s1 + 2 * s2 + 2 * s3 + s4) * (dt / 6)
return du
end
function main()
Time_Step = 14600
member = 200
N = 40
M = 40
F = 8.0
IN = Matrix(1.0I, N, N)
delta = 1.0e-5
u_true = readdlm("L96_truestate.txt")
u_obs = readdlm("L96_observation.txt")
H = Matrix(1.0I, M, M)
R = Matrix(1.0I, M, M)
ua = fill(0.0, (N,member))
uf = fill(0.0, (N,member))
dXf = fill(0.0, (N,member))
open("L96_EnKF_output.txt","w") do output
for m = 1:member
ua[:, m] = rand(N) .+ F
for i = 1:Time_Step
ua[:,m] = Model(view(ua,:,m))
end
end
for i in 1:Time_Step
##forecast step
for m in 1:member
uf[:,m] = Model(view(ua,:,m))
end
dXf = uf .- mean(uf, dims = 2)
Pf = dXf*dXf' / (member-1)
##analysis step
K = Pf*H'*inv(H*Pf*H' + R)
for m in 1:member
ua[:,m] = uf[:,m] + K*(u_obs[i, 2:N+1] - H*uf[:,m])
end
writedlm(output,[(i / 40) (norm(u_true[i, 2:N+1] - mean(ua,dims=2))/sqrt(N)) (norm(u_obs[i, 2:N+1] -u_true[i, 2:N+1])/sqrt(N))])
end
end
end
main()
Forecast step
\begin{align}
x^{f,k} &= M(x^{a,k})\\
\delta X^f &= \left(x^{f,1}-\bar{x}^f, \ldots , x^{f,m} - \bar{x}^f \right) \\
P^f &= \frac{1}{m-1} \delta X^f (\delta X^f)^{\top}
\end{align}
##forecast step
for m in 1:member
uf[:,m] = Model(view(ua,:,m))
end
dXf = uf .- mean(uf, dims = 2)
Pf = dXf*dXf' / (member-1)
ほぼそのままです.view(ua,:,m)としているのは理由は知らないけどこの方が早くなるらしいので.Const参照渡しだと思えばいいんですかね.dXf = uf .- mean(uf, dims = 2)で各列から平均を引くことができます.$\delta X^f$の形を経由しているのはメモリの節約のためで,$N$が非常に大きい場合は$N\times N$行列$P^f$の形にしないで$\delta Y^f = H \delta X^f$として
K = \delta X^f (\delta Y^f)^{\top} \left( \delta Y^f (\delta Y^f)^{\top} + (m-1)R \right)^{-1}
のようにサイズの小さい行列の積の形に書き換えて計算します.
Analysis Step
\begin{align}
K &= P^f H^{\top}(HP^f H^{\top} + R)^{-1}\\
x^{a,k} &= x^{f,k} + K(y - Hx^{f,k})
\end{align}
##analysis step
K = Pf*H'*inv(H*Pf*H' + R)
for m in 1:member
ua[:,m] = uf[:,m] + K*(u_obs[i, 2:N+1] - H*uf[:,m])
end
そのまま書けます.サンプルごとに計算をするのだけ多少面倒です.
結果
横軸に時刻を取り,縦軸に誤差をとってプロットしました.緑が観測の誤差,紫が解析値の誤差です.
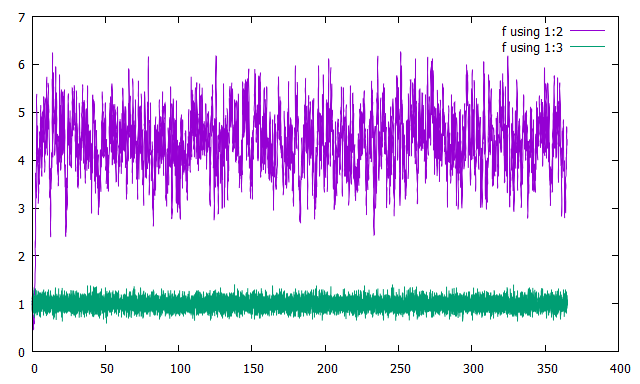
例のFilter Divergenceですね.Inflationをかければ改善されますが,実はそもそもアルゴリズムにミスが指摘されていて,それを修正したのが次のPerturbed Observation Methodです.
EnKF:Perturbed Observation Method
前節のアルゴリズムはKalman Filterのアルゴリズムを素直にアンサンブル平均に書き換えたものです.
なぜうまくいかなかったのかを説明するために,解析誤差共分散$P^a$をアンサンブル平均で計算してみます.
\begin{align}
P^a &= (x^{a,1} - \bar{x}^a,\ldots,x^{a,m}-\bar{x}^a)\times(x^{a,1} - \bar{x}^a,\ldots,x^{a,m}-\bar{x}^a)^{\top}\times \frac{1}{m-1}\\
&= (I-KH) P^f (I-KH)^{\top}
\end{align}
本来は$P^a = (I-KH) P^f (I-KH)^{\top} + KRK^{\top}$となるべきですが,観測$y$の項だけサンプルをとっていないために$KRK^{\top}$の項が抜け落ちています.$(I-KH) P^f (I-KH)^{\top} + KRK^{\top}$のトレースを最小化するように$K$を定めたので,この部分でずれが生じているのです.これを改善したのが次の節で説明するPerturbed Observation Methodです.
アルゴリズム
Analysis Stepだけを修正します.観測$y$の真値$x^t$からの誤差$\varepsilon^o$と同じ分布に従うサンプル$\varepsilon^{o,k}$を取り,次のようにします.
\begin{align}
K &= P^f H^{\top}(HP^f H^{\top} + R)^{-1}\\
x^{a,k} &= x^{f,k} + K(y + \varepsilon^{o,k} - Hx^{f,k})
\end{align}
このように修正すれば$P^a = (I-KH) P^f (I-KH)^{\top} + KRK^{\top}$となることは明らかでしょう.
実装と解説
今回の設定では$N$次元の標準正規分布に従うサンプルをとればよいので,上のEnKF.jlで次のようにAnalysis Stepを書き換えてください.
\begin{align}
K &= P^f H^{\top}(HP^f H^{\top} + R)^{-1}\\
x^{a,k} &= x^{f,k} + K(y + \varepsilon^{o,k} - Hx^{f,k})
\end{align}
##analysis step
K = Pf*H'*inv(H*Pf*H' + R)
for m in 1:member
ua[:,m] = uf[:,m] + K*(u_obs[i, 2:N+1] + randn(N) - H*uf[:,m])
end
結果
横軸に時刻を取り,縦軸に誤差をとってプロットしました.
緑が観測の誤差,紫が解析値の誤差です.
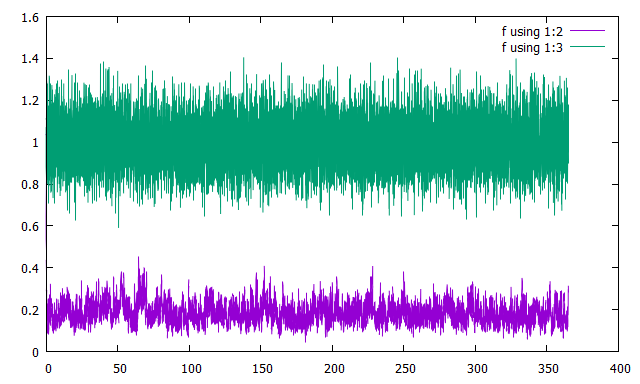
サンプル数が同じでも,Inflationなどしなくてもちゃんとうまくいくことがわかります.
サンプル数を減らしていくとやがてFilter divergenceが起こりますが…
PO法はアルゴリズムが簡単ですが,観測誤差の従う分布はそう簡単に見積もれるわけではないのと,サンプルをとる回数が観測の分も増えるという欠点があります.この欠点を解消するために,サンプルを取らずに済ませる手法が提案されました.それが次節で解説するSquare Root Filterです.
EnKF:Square Root Filter
PO法での観測の摂動を取らなくても済むように,2002年にJeffrey S. WhitakerとThomas M. Hamillによる論文
"Ensemble Data Assimilation without Perturbed Observations"で提案されました.
これを初めて読んだときはPO法のことを知らなかったので,perturbed observationってなんじゃ
と混乱したのを今でも覚えています.
鍵となる考え方は,先ほどまでとは異なり,平均と平均からのずれ(分散)を別々に見積もることです.
導出
PO法でのアルゴリズムを平均と平均からのずれ$x'^{a,k}=x^{a,k}-\bar{x}^a,x'^{f,k} = x^{f,k} - \bar{x}^f$に分けて書くと
\begin{align}
\bar{x}^a &= \bar{x}^f + K(y - H \bar{x}^f) \\
x'^{a,k} &= x'^{f,k} + K(\varepsilon^{o,k} -H x'^{f,k})
\end{align}
となります.平均と平均からのずれを同じ重み$K$を用いて見積もっているわけです.そこで,第二式の$\varepsilon^{o,k}$をなくし,その代わりに上手い$K'$を用いて
\begin{align}
\bar{x}^a &= \bar{x}^f + K(y - H \bar{x}^f) \\
x'^{a,k} &= x'^{f,k} + K'( -H x'^{f,k}) = (I-K'H)x'^{f,k}
\end{align}
の形を仮定します.$K'$は$P^a = (I-K'H)P^f (I-K'H)^{\top}$がトレースの最小値を実現する$(I-KH)P^f$に等しくなるように,すなわち,$(I-K'H)P^f (I-K'H)^{\top} = (I-KH)P^f$を$K'$について解くことで定めます.$K = \delta X^f (\delta Y^f)^{\top} \left( \delta Y^f (\delta Y^f)^{\top} + (m-1)R \right)^{-1}$を用いて計算をすると$I-K'H = \sqrt{I - \delta X^f \left( \delta Y^f (\delta Y^f)^{\top} + (m-1)R \right)^{-1} \delta Y^f}$が得られるので,アルゴリズムは次のようになります.
アルゴリズム
Forecast Step
\begin{align}
x^{f,k} &= M(x^{a,k})\\
\delta X^f &= \left(x^{f,1}-\bar{x}^f, \ldots , x^{f,m} - \bar{x}^f \right) \\
\delta Y^f &= H \delta X^f
\end{align}
Analysis Step
\begin{align}
K &= \delta X^f (\delta Y^f)^{\top} \left( \delta Y^f (\delta Y^f)^{\top} + (m-1)R \right)^{-1} \\
\tilde{K}&=I-(\delta Y^{f})^{\top}\left(\delta Y^{f}\left(\delta Y^{f}\right)^{\top}+(m-1) R\right)^{-1} \delta Y^{f}\\
\bar{u}^a &= \bar{u}^f + K(y - H\bar{u}^f)\\
\delta X^a &= \delta X^f \sqrt{\tilde{K}}\\
u^a &= \delta X^a + (\bar{u}^a,\ldots,\bar{u}^a )
\end{align}
実装と解説
L96_EnKF_SRF_output.txtに結果を出力するプログラムです.サンプルの数は40にしています.
using LinearAlgebra
using Statistics
using Random
using DelimitedFiles
## L96modelの右辺
function L96(u; F = 8.0, N = 40)
f = fill(0.0, N)
for k = 3:N-1
f[k] = (u[k+1] - u[k-2]) * u[k-1] - u[k] + F
end
f[1] = (u[2] - u[N-1]) * u[N] - u[1] + F
f[2] = (u[3] - u[N]) * u[1] - u[2] + F
f[N] = (u[1] - u[N-2]) * u[N-1] - u[N] + F
return f
end
# 4-4Runge-Kutta
function Model(u; dt = 0.05)
du = u
s1 = L96(u)
s2 = L96(u + s1 * dt / 2)
s3 = L96(u + s2 * dt / 2)
s4 = L96(u + s3 * dt)
du += (s1 + 2 * s2 + 2 * s3 + s4) * (dt / 6)
return du
end
function main()
Time_Step = 14600
member = 40
N = 40
M = 40
F = 8.0
IN = Matrix(1.0I, N, N)
delta = 1.0e-5
u_true = readdlm("L96_truestate.txt")
u_obs = readdlm("L96_observation.txt")
H = Matrix(1.0I, M, N)
R = Matrix(1.0I, M, M)
ua = fill(0.0, (N,member))
uf_mean = fill(0.0, N)
ua_mean = fill(0.0, N)
uf = fill(0.0, (N,member))
dXf = fill(0.0, (N,member))
dYf = fill(0.0, (M, member))
dXa = fill(0.0, (N,member))
open("L96_EnKF_SRF_output.txt","w") do output
for m = 1:member
ua[:, m] = rand(N) .+ F
for i = 1:Time_Step
ua[:,m] = Model(view(ua,:,m))
end
end
for i in 1:Time_Step
##forecast step
for m in 1:member
uf[:,m] = Model(view(ua,:,m))
end
uf_mean = mean(uf, dims = 2)
dXf = uf .- uf_mean
dYf = H * dXf
##analysis step
K = dXf*dYf'*inv(dYf*dYf' + (member-1)R)
K_fluc = I - dYf'*inv(dYf*dYf' + (member-1)R)*dYf
ua_mean = uf_mean + K*(u_obs[i, 2:N+1] - H*uf_mean)
dXa = dXf*sqrt(Symmetric(K_fluc))
ua = dXa .+ ua_mean
writedlm(output,[(i / 40) (norm(u_true[i, 2:N+1] - ua_mean)/sqrt(N)) (norm(u_obs[i, 2:N+1] -u_true[i, 2:N+1])/sqrt(N))])
end
end
end
main()
Forecast Step
\begin{align}
x^{f,k} &= M(x^{a,k})\\
\delta X^f &= \left(x^{f,1}-\bar{x}^f, \ldots , x^{f,m} - \bar{x}^f \right) \\
\delta Y^f &= H \delta X^f
\end{align}
##forecast step
for m in 1:member
uf[:,m] = Model(view(ua,:,m))
end
uf_mean = mean(uf, dims = 2)
dXf = uf .- uf_mean
dYf = H * dXf
こちらは何も変わっていません.$\delta Y^f$を計算するようにしただけです.
Analysis Step
\begin{align}
K &= \delta X^f (\delta Y^f)^{\top} \left( \delta Y^f (\delta Y^f)^{\top} + (m-1)R \right)^{-1} \\
\tilde{K}&=I-(\delta Y^{f})^{\top}\left(\delta Y^{f}\left(\delta Y^{f}\right)^{\top}+(m-1) R\right)^{-1} \delta Y^{f}\\
\bar{u}^a &= \bar{u}^f + K(y - H\bar{u}^f)\\
\delta X^a &= \delta X^f \sqrt{\tilde{K}}\\
u^a &= \delta X^a + (\bar{u}^a,\ldots,\bar{u}^a )
\end{align}
##analysis step
K = dXf*dYf'*inv(dYf*dYf' + (member-1)R)
K_fluc = I - dYf'*inv(dYf*dYf' + (member-1)R)*dYf
ua_mean = uf_mean + K*(u_obs[i, 2:N+1] - H*uf_mean)
dXa = dXf*sqrt(Symmetric(K_fluc))
ua = dXa .+ ua_mean
$x'^{a,k}$などは直接持たずに$\delta X^a$を使って計算しなおす形にしています.対称性は丸め誤差で崩れやすいので,$\tilde{K}$の平方根を求めるときは,sqrt(Symmetric(K_fluc))のように対称行列にし直してから平方根をとったほうが良いです.
結果
横軸に時刻を取り,縦軸に誤差をとってプロットしました.
緑が観測の誤差,紫が解析値の誤差です.
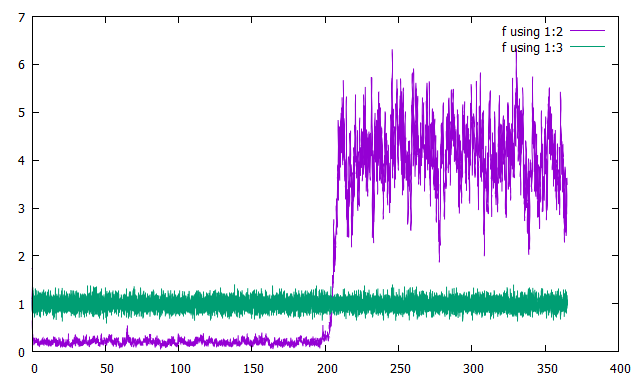
惜しいところまで行っていますがFilter Divergenceを起こしています.
サンプル数40をもう少し増やすと最後まで動くようになります.
Localization
サンプル数は可能な限り減らしたいですが前節のように唐突にFilter divergenceが起こることがあり,なかなか難しいものがあります.これを何とかするために重要なのがLocalizationです.
考え方
本来は予報誤差共分散行列$P^f$の非対角成分は小さいのですが,サンプル数が少ないときは誤差のせいで大きな非対角成分が出てしまいます.これを何とかするために$i,j$成分が例えば$\mathrm{exp}\left(-(i-j)^2 / d)\right)$のようにあらわされる行列
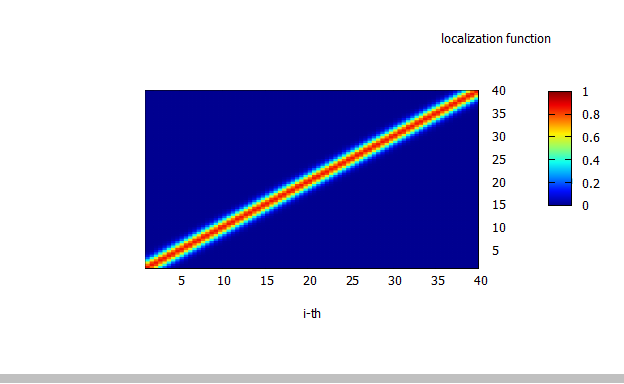
を成分ごとに$P^f$にかけることで非対角成分の誤差を小さくします.
実装と解説
EnKF_PO.jlでlocalizationを行います.
\mathrm{exp}\left(-(i-j)^2 / d)\right)
function localization(i,j; dist = 2.0)
return exp(-(i-j)^2 / dist)
end
こんな感じに関数を準備しておいて,localization_matに行列として持たせておきます.
##forecast step
for m in 1:member
uf[:,m] = Model(view(ua,:,m))
end
dXf = uf .- mean(uf, dims = 2)
Pf = dXf*dXf' / (member-1)
Pf = localization_mat .* Pf
Forecast Stepの最後にPf = localization_mat .* Pfでlocalizationを行います..*で成分ごとに掛け算するだけです.
結果
memberを40としてlocalizationを行ったグラフを示します.
横軸に時刻を取り,縦軸に誤差をとってプロットしました.
緑が観測の誤差,紫が解析値の誤差です.
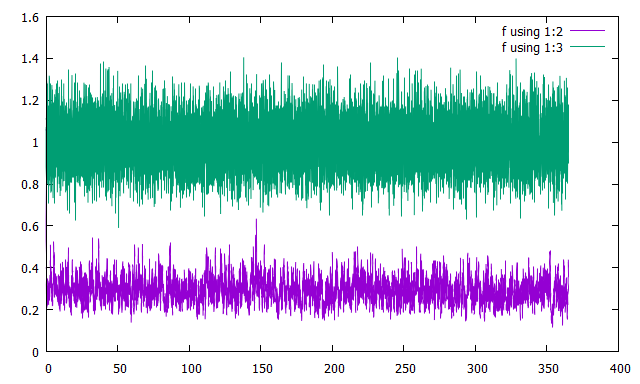
サンプル数を200から40に減らしてもlocalizationをかければ動作することがわかります.今回はlocalizationの関数を正規分布のような形でとりましたが,これが最適というわけではないです.いろいろ工夫してInflationと組み合わせればRMSEの時間平均を0.2程度まで落とすことができます.一般に最適なlocalizationの形を探すのは厄介な仕事になりますが,少ないサンプル数でも動かせるようになるのは非常に魅力的です.
まとめ
今回はEnKFの基本的な手法であるPO法,SRFを解説しました.
次回以降の記事ではEAKF,ETKF,そして大自由度系でも使われるLETKFの解説をする予定です.