More than 1 year has passed since last update.

Igor_FFTスペクトルの波長軸表示

Igor

Last updated at 2022-09-25Posted at 2022-09-25

Igorを用いてデータのFFTを行い、デフォルトの周波数軸ではなく波長軸で表示するためのProcedureです。サンプルとして上のグラフのような波束を作り、FFT後の下のようなスペクトルを表示します。

Function LightFFT()
Variable Cell_Num	= 10000
Variable C_light = 299792458
Variable Max_t,dt
	Max_t	=50e-15
	dt		= Max_t*2/Cell_Num
Variable Freq_1,Freq_2
	Freq_1	= 375e12
	Freq_2	= 193e12
Variable A_1,A_2,W_1,W_2,t_1,t_2
	A_1		= 1
	W_1		= 10e-15
	t_1		= 10e-15
	A_2		= 2
	W_2		= 15e-15
 	t_1		= -20e-15
String LightName = "t_light"
	Make/o/d/n = (Cell_Num) $(LightName)
	Wave LightWave = $(LightName)
		setscale/p x,-Max_t,dt, LightWave
		LightWave = 0
		LightWave += A_1*exp(-((x-t_1)/W_1)^2)*sin(Freq_1*x*2*pi)
		LightWave += A_2*exp(-((x-t_2)/W_2)^2)*sin(Freq_2*x*2*pi)
///////////////////////////////////////////////////////////////
String FFTName	= "Spec_Light"
	Redimension/n=1e6 LightWave
	FFT/OUT=3/DEST=$(FFTName)	LightWave
	Wave SpecWave = $(FFTName)
	Duplicate/o SpecWave WLaxis
		WLaxis = C_light/x
		Redimension/n=5e4 SpecWave,WLaxis
		Redimension/n=(Cell_Num) LightWave
////////////////////////////////////////////////////////////////
		Display/k=1 SpecWave vs WLaxis
		setaxis bottom 0,3e-6
		Label left "Intensity [a.u.]";DelayUpdate
		Label bottom "Wavelength [μm]";DelayUpdate
		ModifyGraph tick=2,mirror=2,prescaleExp(bottom)=6,btLen=3
end

①サンプルWaveの作成
FFTを実行するために適当な波を作ります。今回は波長800 nmと1.55 μmの二つのパルスの和にしています。シミュレーションソフトやオシロスコープなどで取得したデータを用いても問題ありません。ただし、ほとんどのシミュレーションソフトや実験データは時間波形データと時間軸データが別に出力されているため、FFTを実行する前に時間軸を合わせる必要があります。Igorに読み込んだ時点では全てのWaveのdeltaはデフォルトの1になっており、そのままFFTを実行すると1セル=1秒とみなしたFFTを行ってしまいます。
上記Procedure中のsetscale/p x,-Max_t,dt, LightWaveが時間軸合わせに該当する箇所となっています。-Max_tは波形の開始時間、dtは時間間隔、LightWaveは対象とする波を示しています。
例えば、Wave0という時間軸データとWave1という実験波形データを読み込んだ場合であれば行う時間軸調整は

Variable Start_t,Step_t
    Start_t = Wave0[0]
    Step_t  = Wave0[1]-Wave0[0]
    setscale/p x,Start_t,Step_t, Wave1

となると思います。(時間軸データが線形な場合に限ります。非線形な時間軸データの場合今のところ対処する手段は不明です。)

②FFT及び波長軸の作成
　適切な時間軸調整を行っていた場合、FFTで直ちにHzを軸とする波が出力されます。

上記画像はこの時点で出力された波ですが、1 THz = 1e12Hzなので作成した波が問題なくFFTされていることが確認できます。THzで表示したい場合にはAxis propertiesのExponent prescaleを調節することで表示できます。(https://qiita.com/linear_tree/items/6c1e5852db29d3b8178e)
　なお、今回はoutput形式を一番単純なMagnitudeにしましたが、複素形式で出力したい場合にはFFT/OUT=3/DEST=$(FFTName) LightWaveのOUT=3を3ではなく1にします。ほかにどんな出力形式があるかはAnalysis→Transforms→Fourier Transforms→Output typesで確認できます。
　また、一般にシミュレーションで光波束を扱う時などはおおむね一振動当たり8~10点程度の点数があれば十分なのでfsスケールのシミュレーション結果などは0.1 fsスケールほどのデータ間隔で出力することが多いですが、IgorでFFTをかけた場合の出力されるスペクトルの最小単位はもとの時間波形データのセル数と時間間隔で決まる(1/(Rows×delta))ため、出てきたスペクトルが粗すぎる場合にはFFTの直前にセル数を増やしておくなどの処理をする必要があります。今回のFunctionではFFTの直前にRedimension/n=1e6 LightWaveでセル数を増やし、FFT後にRedimension/n=(Cell_Num) LightWaveで戻しています。

③表示
特記事項は特にありません。強いて言うと最初にコマンド打ち込みもしくはNewGraphから波長軸グラフを出力すると下画像のような見ための画像が表示されるためなにかミスがあったかと思ってしまうのですが表示範囲が異常に広いだけなのでhorizontal axisを拡大すれば適切なスペクトルが表示されます。

(https://qiita.com/linear_tree/items/19789d96ed42641d5d75)

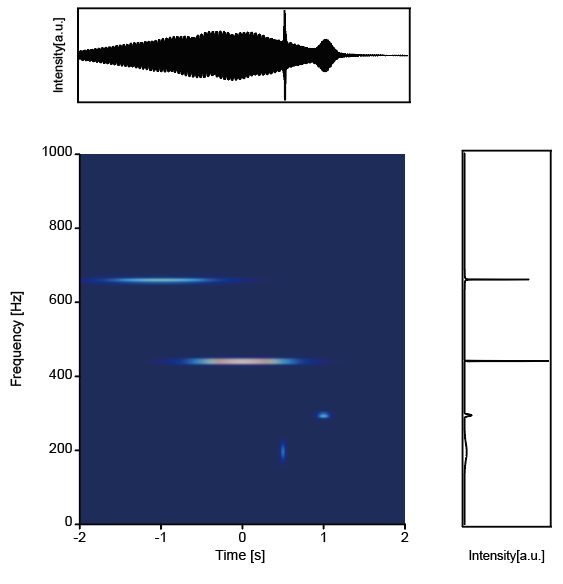
下記は需要が極端に少ない完全な蛇足ですが

4種類の周波数の音を混ぜたサンプル波の作成
FFTでスペクトルを取得
Wigner変換で時間-周波数スペクトログラムを取得
全て一度に表示
を行うためのFunctionです。今回は光ではなく音の周波数領域で作成しています。

Function SoundFFT()

Variable Cell_Num	= 8000
Variable Max_t,dt
	Max_t	=2
	dt		= Max_t*2/Cell_Num
Variable Freq_1,Freq_2,Freq_3,Freq_4
	Freq_1	= 659
	Freq_2	= 440
	Freq_3	= 294
	Freq_4	= 196 
Variable A_1,A_2,A_3,A_4,W_1,W_2,W_3,W_4,t_1,t_2,t_3,t_4
	A_1		= 10
	W_1		= 1
	t_1		= -1
	A_2		= 15
	W_2		= 0.8
	t_2		= 0
	A_3		= 10
	W_3		= 0.1
	t_3		= 1
	A_4		= 30
	W_4		= 0.01
	t_4		= 0.5
	
String SoundName = "t_sound"
	Make/o/d/n = (Cell_Num) $(SoundName)
	Wave SoundWave = $(SoundName)
		setscale/p x,-Max_t,dt, SoundWave
		SoundWave = 0
		
		SoundWave += A_1*exp(-((x-t_1)/W_1)^2)*sin(Freq_1*x*2*pi)
		SoundWave += A_2*exp(-((x-t_2)/W_2)^2)*sin(Freq_2*x*2*pi)
		SoundWave += A_3*exp(-((x-t_3)/W_3)^2)*sin(Freq_3*x*2*pi)
		SoundWave += A_4*exp(-((x-t_4)/W_4)^2)*sin(Freq_4*x*2*pi)

String FFTName	= "Spec_sound"
String WigName	= "Wigner_sound"
	FFT/OUT=3/DEST=$(FFTName)	SoundWave
	Wignertransform/Gaus=0.1/dest=$(WigName) SoundWave
	
end

Function DispSound()

String TimeName		= "T_sound"
String FFTName		= "Spec_sound"
String WigName		= "Wigner_sound"
	Wave TimeWave	= $(TimeName)
	Wave FFTWave 	= $(FFTName)
	Wave Wigner		= $(WigName)
	Display/k=1/W=(0,0,400,400)
	Display/W=(0,100,300,400)/host=#
		AppendIMage Wigner
		ModifyImage Wigner_sound ctab= {*,*,Geo,0}
		ModifyGraph standoff=0,btLen=3
		Label left "Frequency [THz]"
		Label bottom "Time [s]"
	Display/W=(300,100,400,400)/host=##
		Appendtograph FFTWave
		ModifyGraph SwapXY=1
		ModifyGraph mirror=2,nticks=0,btLen(bottom)=4,btLen(left)=1
		Label bottom "Intensity[a.u.]"
		ModifyGraph rgb=(0,0,0)
	Display/W=(30,0,300,100)/host=##
		Appendtograph TimeWave
		Label left "Intensity[a.u.]"
		Label bottom " "
		ModifyGraph mirror=2,nticks=0,btLen(bottom)=3,btLen(left)=1
		ModifyGraph rgb=(0,0,0)
end

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up