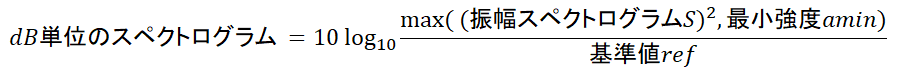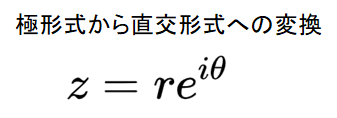LibROSAとは

LibROSAはPythonの音声処理ライブラリです。
様々な音声処理を簡潔に記述できます。
今回は以下の音声処理の基本処理をまとめました。
- 音声の読み込み
  - 周波数を指定して音声を読み込み
  - Notebook上で、音声をプレーヤーで再生
  - 音声波形のグラフを表示
- スペクトログラムへの変換
  - STFTで音声からスペクトログラムへ変換
  - 強度をdB単位に変換
  - スペクトログラムのカラープロットを表示
- 音声を復元
  - 逆STFTでスペクトログラムから音声を復元する場合
  - 位相情報を推定して音声を復元する場合

ソースコード：https://github.com/lilacs2039/ColabNotebooks/blob/master/audio/LibROSA%E4%BD%BF%E3%81%84%E6%96%B9.ipynb

初期化

import os
from tqdm import tqdm
import numpy as np
import matplotlib.pyplot as plt
import IPython.display
from IPython.display import display
import pandas as pd

import librosa
import librosa.display

# pyplotのデフォルト値を設定
plt.rcParams.update({
  'font.size' : 10
  ,'font.family' : 'Meiryo' if os.name == 'nt' else ''  # Colabでは日本語フォントがインストールされてないので注意
  ,'figure.figsize' : [10.0, 5.0]
  ,'figure.dpi' : 300
  ,'savefig.dpi' : 300
  ,'figure.titlesize' : 'large'
  ,'legend.fontsize' : 'small'
  ,'axes.labelsize' : 'medium'
  ,'xtick.labelsize' : 'small'
  ,'ytick.labelsize' : 'small'
  })
# ndarrayの表示設定
np.set_printoptions(threshold=0)  # 可能ならndarrayを省略して表示
np.set_printoptions(edgeitems=1)  # 省略時に１つの要素だけ表示

音声の確認

読み込み

librosaに標準で入っている音声ファイルを読込みます。¹

audio_path = librosa.util.example_audio_file(); audio_path

出力

    '（ホームディレクトリなど）\\anaconda3\\lib\\site-packages\\librosa\\util\\example_data\\Kevin_MacLeod_-_Vibe_Ace.ogg'

librosa.load() ドキュメント　https://librosa.org/librosa/master/generated/librosa.core.load.html

y, sr = librosa.load(audio_path)  # サンプリング周波数　22.05kHzで読み込み
# y, sr = librosa.load(librosa.util.example_audio_file(), sr=None)  # 元の音声ファイルのサンプリング周波数で読み込む場合
# y, sr = librosa.load(librosa.util.example_audio_file(), sr=4096)  # 約4kHzでリサンプリングして読み込む場合
print([type(y), y.shape], [type(sr), sr])

出力

    [<class 'numpy.ndarray'>, (1355168,)] [<class 'int'>, 22050]

サンプリング周波数srについて

srはSampling Rate（サンプリング周波数）の略です。１秒間の音声を何個のデータで表すかを示します。（↑の例では22050データ/秒）
- 全データ数y.size = sr × 再生時間　が成り立ちます。
srを指定しない場合、読み込んだファイルのサンプリング周波数に関わらず、22.05kHzにリサンプリングして読み込みます。　←　【初見注意】
sr=None　を指定すると、元ファイルのサンプリング周波数で読み込みます。
sr=値　を指定すると、指定したサンプリング周波数で読み込みます。

音声をプレーヤーで確認

IPython.display.display()　ドキュメント https://ipython.readthedocs.io/en/stable/api/generated/IPython.display.html#IPython.display.display
IPython.display.Audio() ドキュメント https://ipython.readthedocs.io/en/stable/api/generated/IPython.display.html#IPython.display.Audio

音声はBase64エンコーディングしてJupyter Notebookに埋め込まれます。（重いので本記事では置き換えました）

display(IPython.display.Audio(y, rate=sr))

librosa音声変換記事 https://t.co/CedmBGtHfS

Vibe Ace (Kevin MacLeod) / CC BY 3.0 pic.twitter.com/eMkYzYU3af
— lilacs2039 (@lilacs2039) July 5, 2020

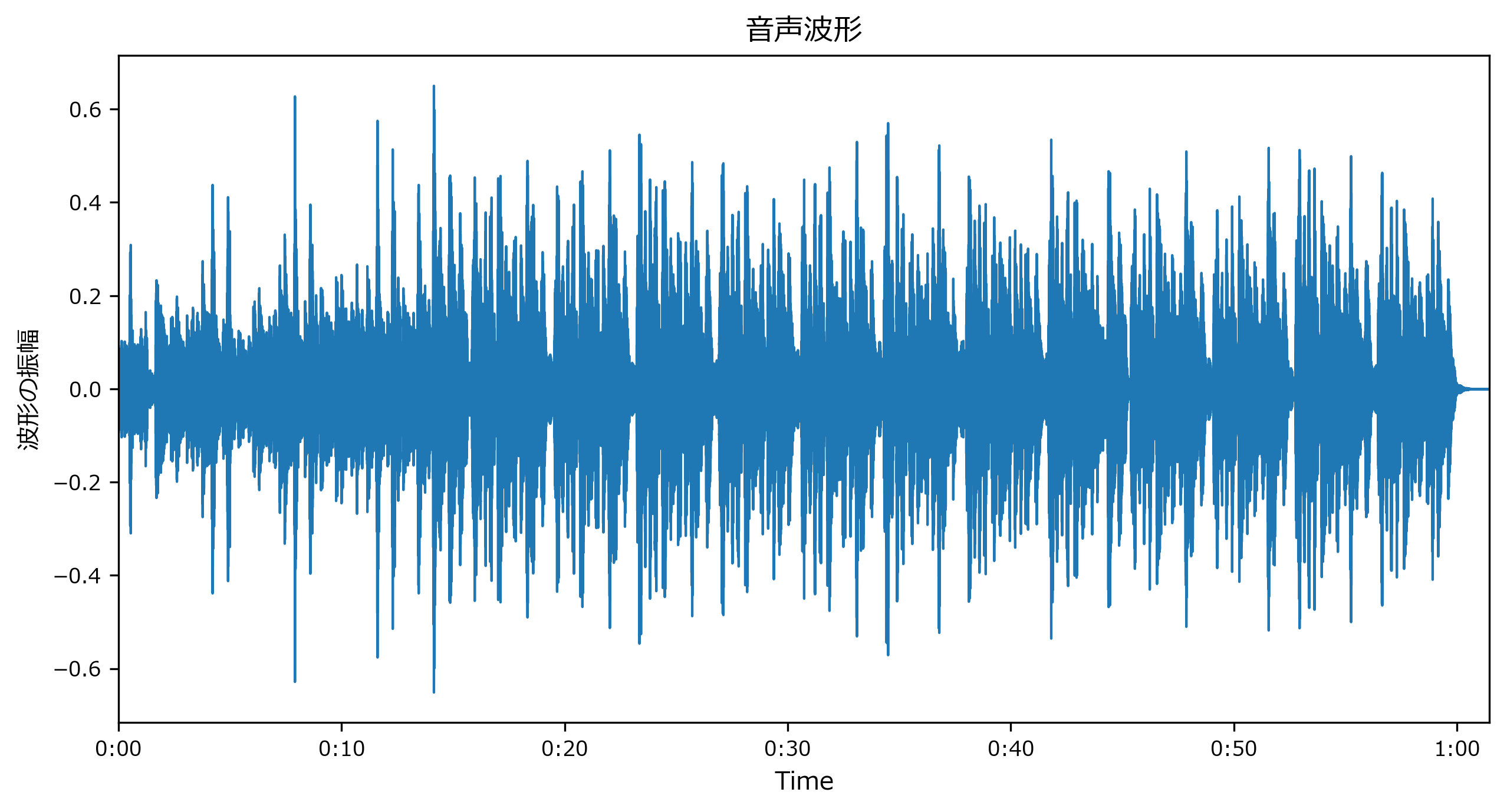
音声波形表示

librosa.display.waveplot() ドキュメント　https://librosa.org/librosa/master/generated/librosa.display.waveplot.html

mpl_collection = librosa.display.waveplot(y, sr=sr)
mpl_collection.axes.set(title="音声波形", ylabel="波形の振幅")

出力

    [Text(0, 0.5, '波形の振幅'), Text(0.5, 1.0, '音声波形')]

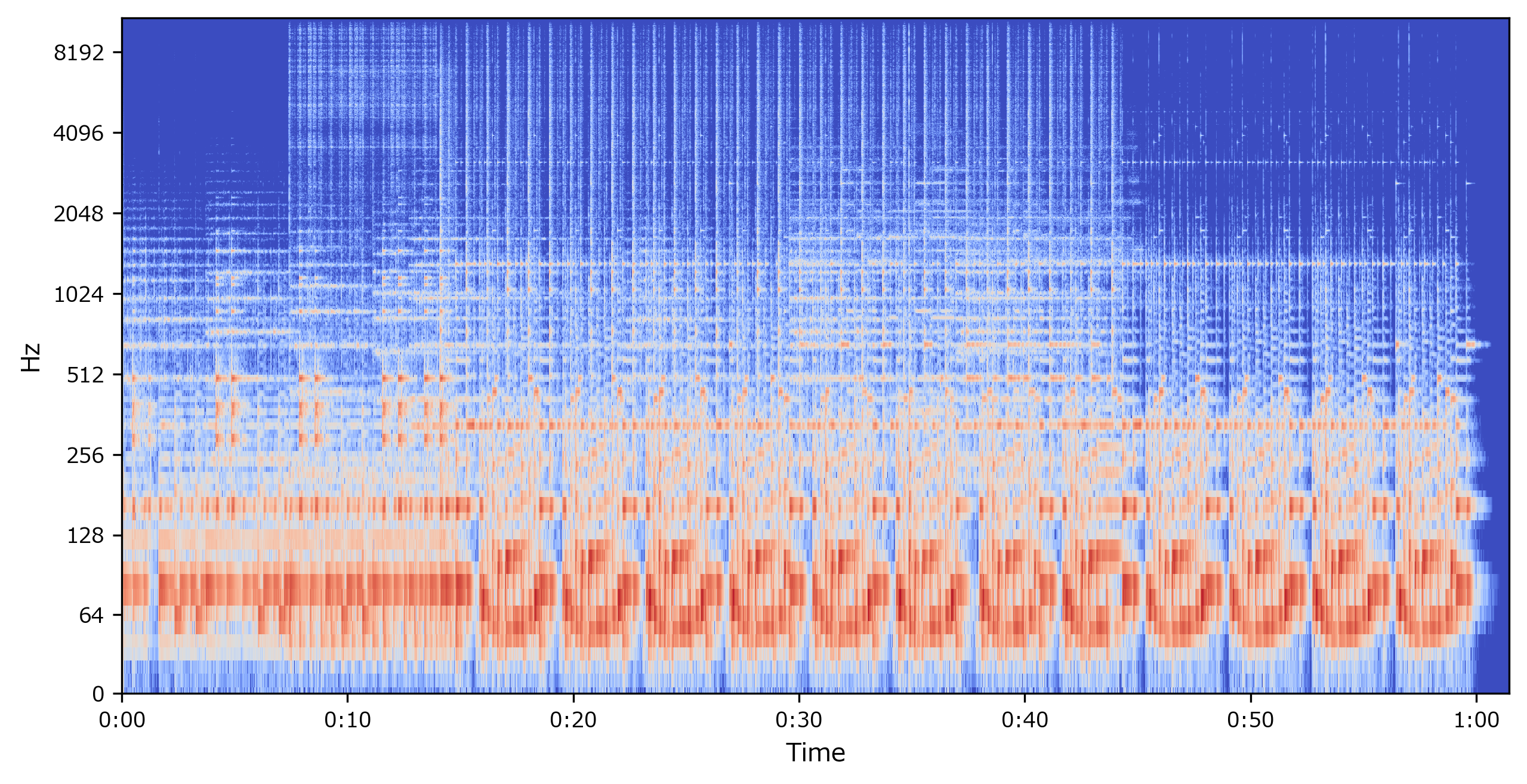
スペクトログラムへの変換

音声信号に「短時間フーリエ変換（Short-time Fourier transform : STFT）」を行うことでスペクトログラムが得られます。
スペクトログラムとは、音声を周波数スペクトルの時間経過で示したものです。

スペクトログラムの計算・表示

D = librosa.stft(y)  # STFT
S, phase = librosa.magphase(D)  # 複素数を強度と位相へ変換
Sdb = librosa.amplitude_to_db(S)  # 強度をdb単位へ変換
librosa.display.specshow(Sdb, sr=sr, x_axis='time', y_axis='log')  # スペクトログラムを表示

出力

    <matplotlib.axes._subplots.AxesSubplot at 0x1cb80c833c8>

やっていること

STFT

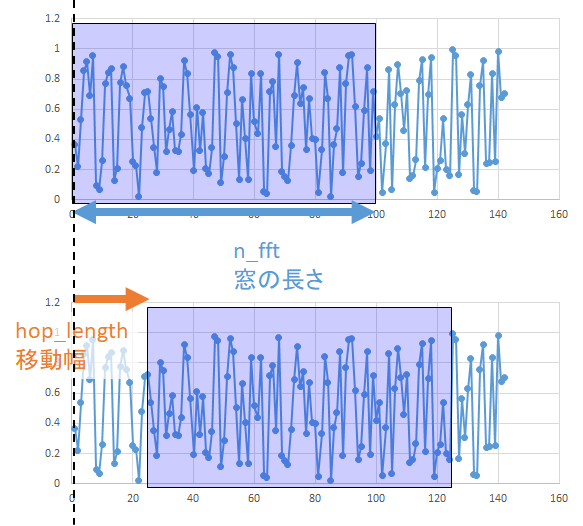
STFTの手順
- 音声信号のある時間範囲を窓で区切ってフーリエ変換して、その時間範囲の周波数スペクトルを計算します。
- 窓をずらしながら繰り返すことで、周波数スペクトルの時間経過の行列Dが得られます。
STFTの主なパラメータ
- n_fft（窓の長さ）
  - デフォルト値は2048
- hop_length（窓の移動幅）
  - デフォルト値はn_fft/4

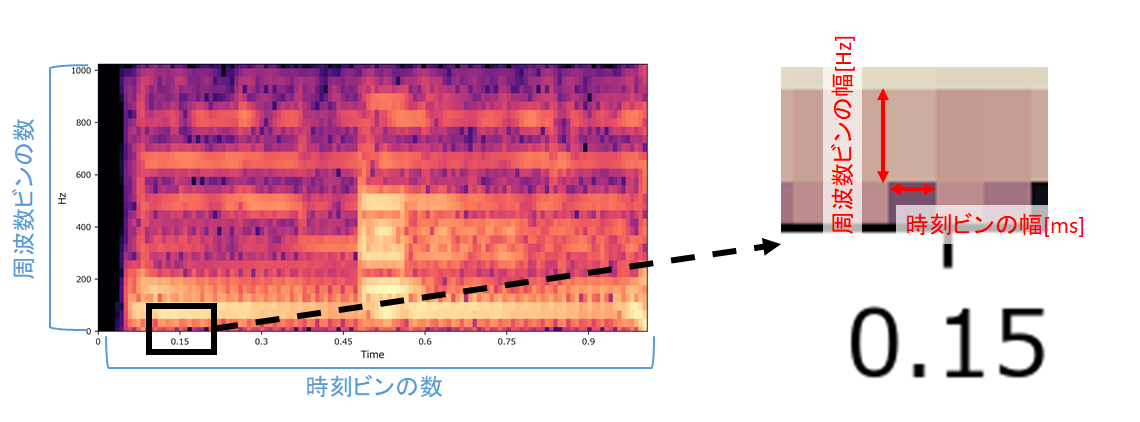
周波数ビン・時刻ビンの計算方法

スペクトログラム計算結果のイメージ

「周波数ビンの数」「時刻ビンの数」「周波数ビンの幅」「時刻ビンの幅」は以下のように計算できます。
サンプリング定理から、音声の周波数はサンプリング周波数/2までしか表現できません。

計算例
デフォルト値において、librosa.stft()は以下のような仕様になることがわかります。
- 0Hz～約11kHzの範囲を約1025分割して表現（周波数分解能は約10.76Hz）
- １秒間を約43分割して表現（時間分解能は約23.26ms）
srやn_fftを調整して目標の分解能やデータサイズが実現できます。

STFTの出力の行列`D`の確認

librosa.stft()　ドキュメント https://librosa.org/librosa/master/generated/librosa.core.stft.html

D = librosa.stft(y)  # STFT
print(type(D), D.shape)
print(D)

出力

    <class 'numpy.ndarray'> (1025, 2647)
    [[ 2.5802802e-03-0.j ...  7.2303657e-05-0.j]
     ...
     [-1.7063057e-07-0.j ... -5.1327298e-09-0.j]]

STFTで得られたDは複素数の２次元ndarray ※ であることがわかります。

※　「２次元」ではなく「２階のテンソル」と呼ぶ方が正しいかもしれませんが、本記事では２次元で統一します。

複素数を強度と位相へ変換

複素数の行列Dを、強度の行列Sと位相の行列phaseに変換します。

librosa.magphase() ドキュメント https://librosa.org/librosa/master/generated/librosa.core.magphase.html

S, phase = librosa.magphase(D)  # 複素数を強度と位相へ変換

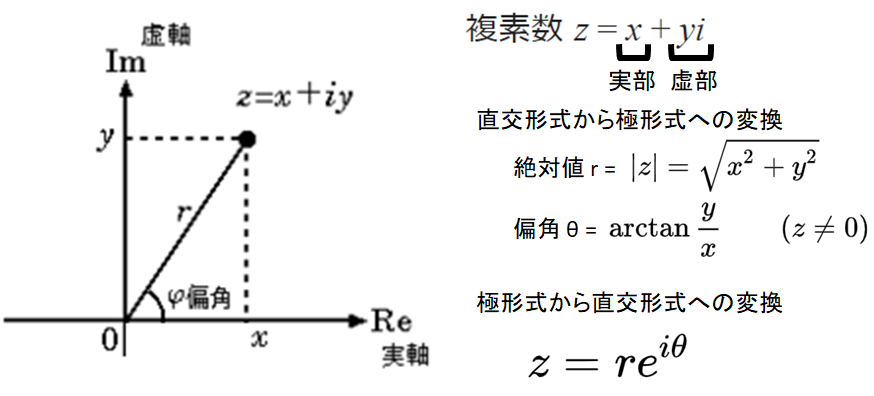
librosa.magphase(D)がやっていること
- STFTで得られた行列Dの複素数は直交形式ですが、スペクトログラムは極形式（絶対値 r: 強度, 偏角 θ: 位相）が望ましいです。
- そこで、複素数を「直交形式から極形式へ変換」しています。
- 参考：複素平面～ wikipedia https://ja.wikipedia.org/wiki/%E8%A4%87%E7%B4%A0%E5%B9%B3%E9%9D%A2

強度の行列`S`の確認

print(type(S), S.shape)
print(S)

出力

    <class 'numpy.ndarray'> (1025, 2647)
    [[2.5802802e-03 ... 7.2303657e-05]
     ...
     [1.7063057e-07 ... 5.1327298e-09]]

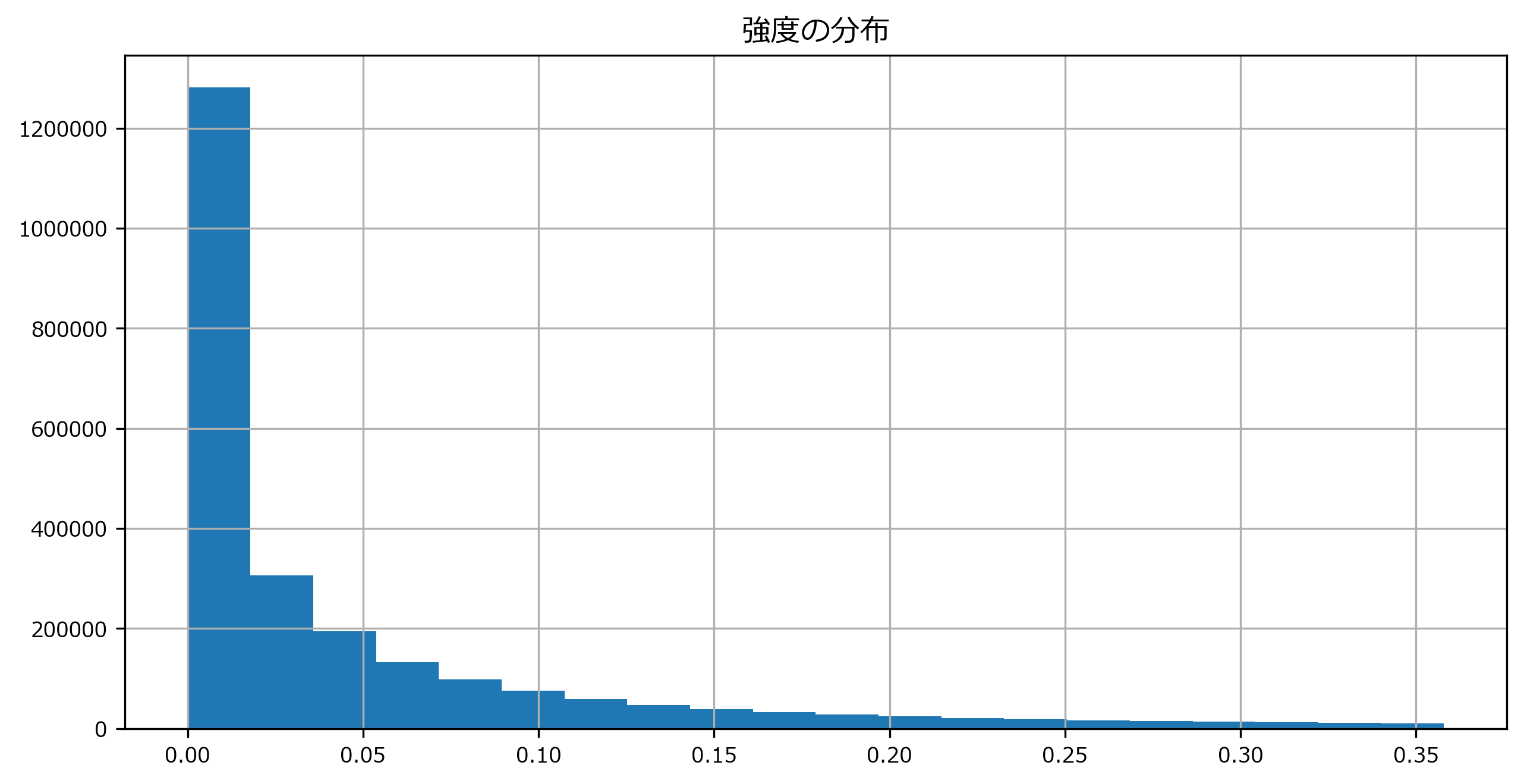
s = pd.DataFrame(S.flatten())
s.hist(bins=20, range=(s.min().values[0],s.quantile(0.9).values[0]) ) # Sの最小値～90%点までの分布を表示
plt.title("強度の分布")

出力

    Text(0.5, 1.0, '強度の分布')

強度の行列Sは、２次元ndarrayで各要素は0より大きい実数であることがわかります。

位相の行列`phase`の確認

print(type(phase), phase.shape)
print(phase)

出力

    <class 'numpy.ndarray'> (1025, 2647)
    [[ 1.+0.000000e+00j ...  1.+0.000000e+00j]
     ...
     [-1.+8.742278e-08j ... -1.+8.742278e-08j]]

p = pd.DataFrame(phase.flatten()).sample(n=1000)  # 散布図にするにはデータ数多すぎなので、1000データをランダムサンプリング
mpl_collection = plt.scatter(np.real(p), np.imag(p))
mpl_collection.axes.set(title="複素平面上の位相の散布図", xlabel="実部", ylabel="虚部", aspect='equal')

出力

    [Text(0, 0.5, '虚部'), Text(0.5, 0, '実部'), Text(0.5, 1.0, '複素平面上の位相の散布図'), None]

位相の行列phaseは、２次元ndarrayで各要素は絶対値１, 偏角θの複素数であることがわかります。

強度をdb単位へ変換

スペクトログラムの強度が線形スケールで扱いづらい場合は、dB単位に変換して対数スケールで扱えるようにします。
dB単位では、+20dBで（振幅）スペクトログラムの強度は10倍になります。

librosa.amplitude_to_db() ドキュメント https://librosa.org/librosa/master/generated/librosa.core.amplitude_to_db.html

Sdb = librosa.amplitude_to_db(S)  # 強度をdb単位へ変換

`librosa.amplitude_to_db()`がやっていること

下式で、振幅スペクトログラムをdB単位に変換します。

主なパラメータ
- 最小値amin
  - 計算式のlogの中身が0のとき戻り値が-∞とならないように、最小値を指定
  - デフォルト値　1e-5
- 基準値ref
  - スペクトログラムの２乗 = refのとき、0dBとなるように変換する。
  - デフォルト値 1

dB単位の強度の行列`Sdb`の確認

print(type(Sdb), Sdb.shape)
print(Sdb)

出力

    <class 'numpy.ndarray'> (1025, 2647)
    [[-33.29261 ... -33.29261]
     ...
     [-33.29261 ... -33.29261]]

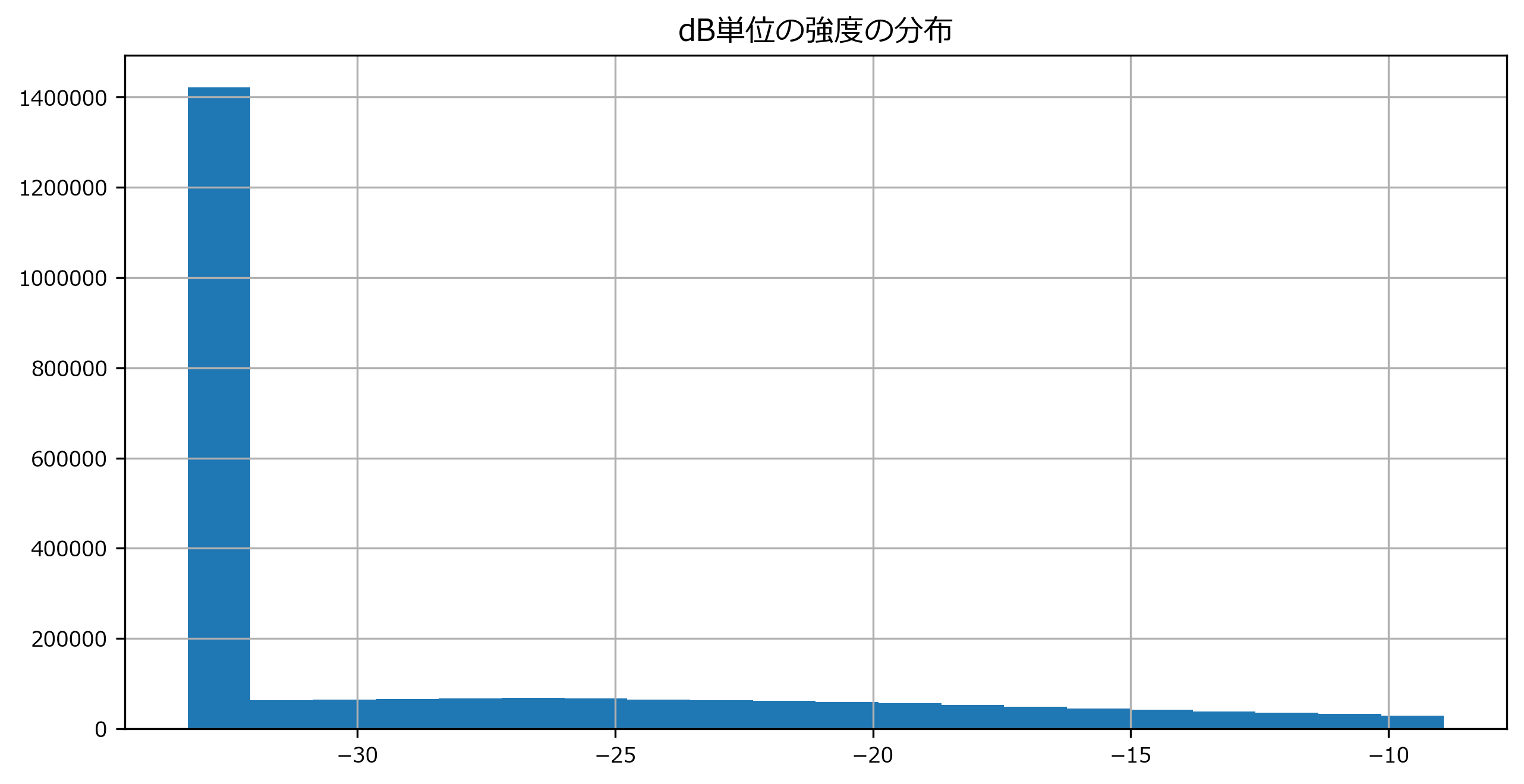
sdb = pd.DataFrame(Sdb.flatten())
sdb.hist(bins=20, range=(sdb.min().values[0], sdb.quantile(0.9).values[0]) ) # Sの最小値～90%点までの分布を表示
plt.title("dB単位の強度の分布")

出力

    Text(0.5, 1.0, 'dB単位の強度の分布')

スペクトログラムを表示

周波数と強さは線型目盛でも対数目盛でもよく、用途によって使い分けます。

librosa.display.specshow() ドキュメント https://librosa.org/librosa/master/generated/librosa.display.specshow.html

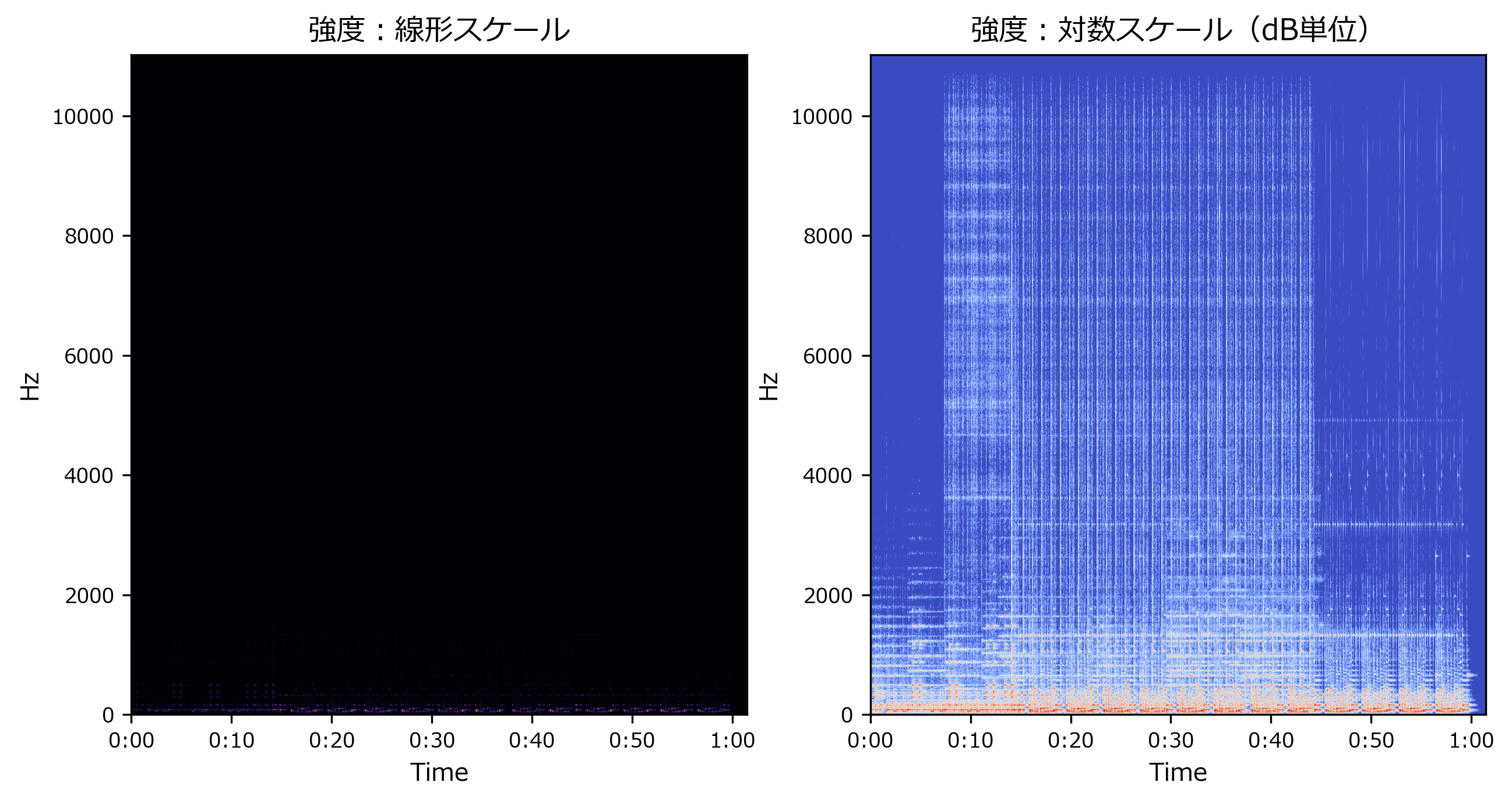
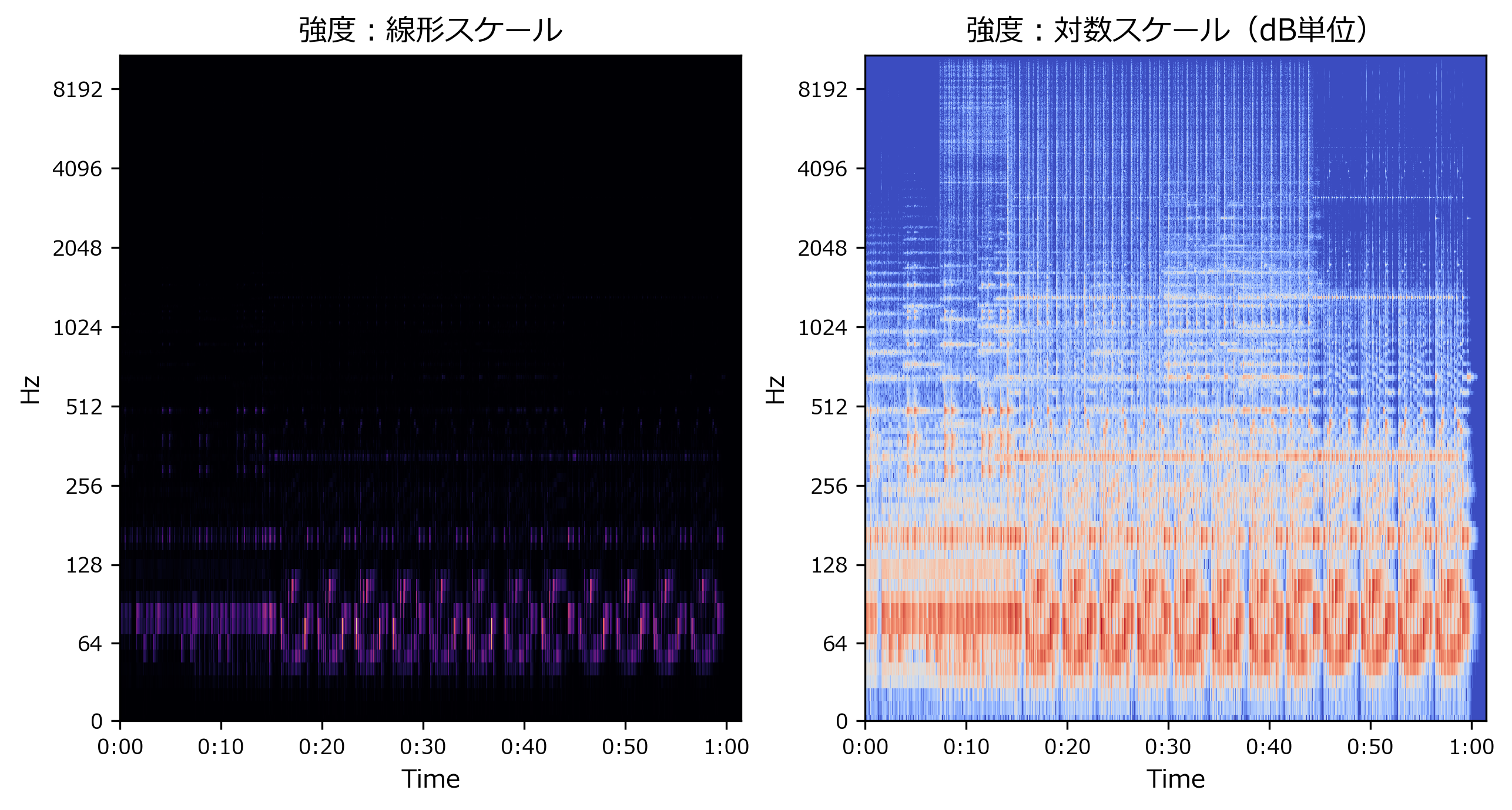
周波数：線形スケール

librosa.display.specshow()の引数に、y_axis='hz'を指定します

fig,axes = plt.subplots(nrows=1,ncols=2)
axes[0].set_title("強度：線形スケール")
librosa.display.specshow(S, sr=sr, x_axis='time', y_axis='hz', ax=axes[0])
axes[1].set_title("強度：対数スケール（dB単位）")
librosa.display.specshow(Sdb, sr=sr, x_axis='time', y_axis='hz', ax=axes[1])

出力

    <matplotlib.axes._subplots.AxesSubplot at 0x1cb81bed2c8>

周波数：対数スケール

librosa.display.specshow()の引数に、y_axis='log'を指定します

fig,axes = plt.subplots(nrows=1,ncols=2)
axes[0].set_title("強度：線形スケール")
librosa.display.specshow(S, sr=sr, x_axis='time', y_axis='log', ax=axes[0])
axes[1].set_title("強度：対数スケール（dB単位）")
librosa.display.specshow(Sdb, sr=sr, x_axis='time', y_axis='log', ax=axes[1])

出力

    <matplotlib.axes._subplots.AxesSubplot at 0x1cb81ca9408>

（おまけ）位相スペクトログラム

# 位相`phase`（直交形式）から偏角θを計算してカラープロット
ax = librosa.display.specshow(np.arctan2(np.imag(phase), np.real(phase)), sr=sr, x_axis='time', y_axis='hz')
ax.axes.set_ylabel("Phase")
plt.title("位相スペクトログラム")

出力

    Text(0.5, 1.0, '位相スペクトログラム')

ランダムノイズのようにしか見えません。パターンを見出すのは難しそうです。

周波数・時間分解能の調整例

やること
- 最初の60秒に対して、0~1kHzの範囲を時間分解能10ms程度で確認したい
手順
- 約2kHzでリサンプリング　→　n_fftを調整してSTFT、強度スペクトログラムを表示（周波数は線形スケール、強度はdB単位）
スペクトログラムのビン形状・分解能の予測値

playtime2, sr2, n_fft2, hop_length2 = 60, 2048, 64, 64//4  # パラメータ
y2 = librosa.resample(y[0:sr * playtime2],sr,sr2)
D2 = librosa.stft(y2,n_fft=n_fft2, hop_length=hop_length2)  # hop_lengthはデフォルト値と同じ計算にしたので、指定しなくても同じ。
S2, _ = librosa.magphase(D2)  # 複素数を強度と位相へ変換
Sdb2 = librosa.amplitude_to_db(S2)  # 強度をdb単位へ変換
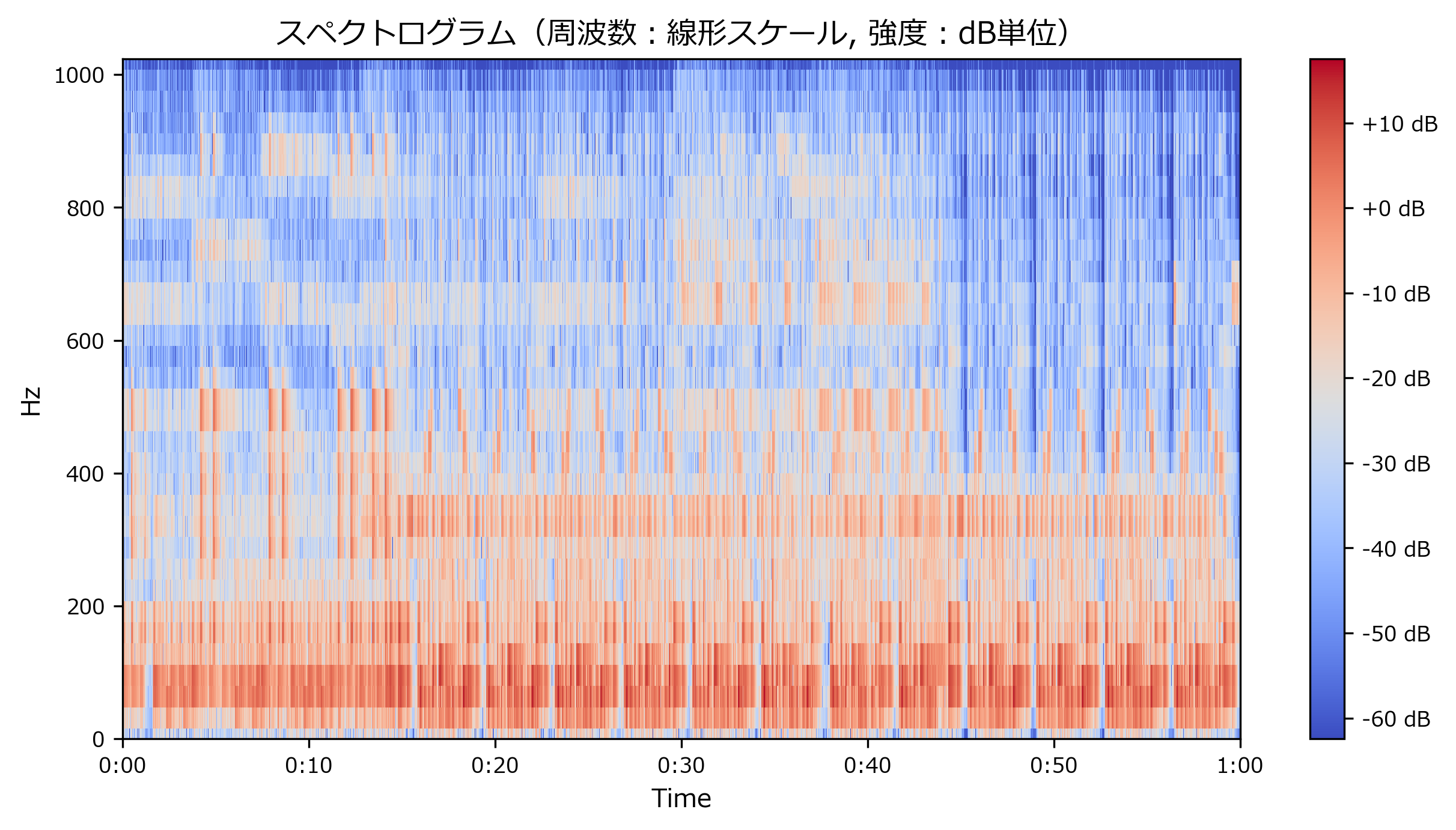
tmp = librosa.display.specshow(Sdb2, sr=sr2, hop_length=hop_length2, x_axis='time', y_axis='hz')  # スペクトログラムを表示
plt.title("スペクトログラム（周波数：線形スケール, 強度：dB単位）")
plt.colorbar(format='%+2.0f dB')

出力

    <matplotlib.colorbar.Colorbar at 0x1cbb67bec08>

print("予測ビン形状 : \t", (33, 128 * playtime2))
print("実際のビン形状 :\t", Sdb2.shape)

出力

    予測ビン形状 : 	 (33, 7680)
    実際のビン形状 :	 (33, 7681)

スペクトログラムのビンの形状は、計算式で予測した値と大体あっていることが確認できます。

音声の復元

位相情報が使える場合：librosa.istft()

手順
- 下式で、強度S,位相phaseから直交形式の複素数の行列Dへ変換
- ISTFTでスペクトログラムを音声に復元します。
逆短時間フーリエ変換（Inverse short-time Fourier transform : ISTFT)
librosa.istft() ドキュメント https://librosa.org/librosa/master/generated/librosa.core.istft.html?highlight=istft#librosa.core.istft

D = S * np.exp(1j*phase)  # 直交形式への変換はlibrosaの関数ないみたいなので、自分で計算する。
y_inv = librosa.istft(D)
display(IPython.display.Audio(y_inv, rate=sr))
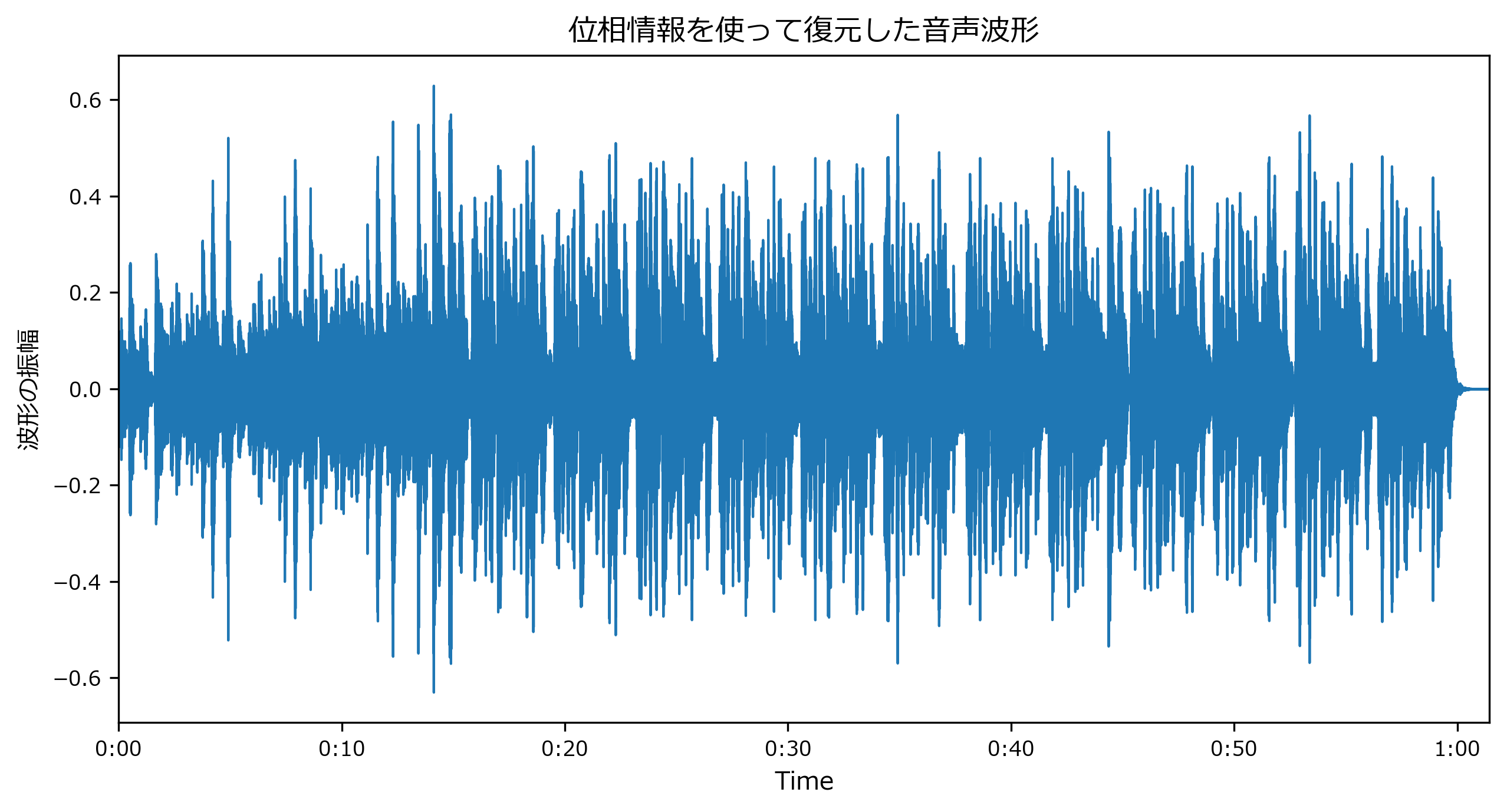
mpl_collection = librosa.display.waveplot(y_inv, sr=sr)
mpl_collection.axes.set(title="位相情報を使って復元した音声波形", ylabel="波形の振幅")

出力

    [Text(0, 0.5, '波形の振幅'), Text(0.5, 1.0, '位相情報を使って復元した音声波形')]

librosa音声変換記事 https://t.co/CedmBGtHfS

Vibe Ace (Kevin MacLeod) / CC BY 3.0 pic.twitter.com/qaTaR4u7dt
— lilacs2039 (@lilacs2039) July 5, 2020

ylim = ax.axes.set_ylim(); ylim  # 次の比較用にy軸の範囲を保存

出力

    (-0.6926389932632446, 0.6926389932632446)

位相情報が使えない場合：griffinlim()で位相推定

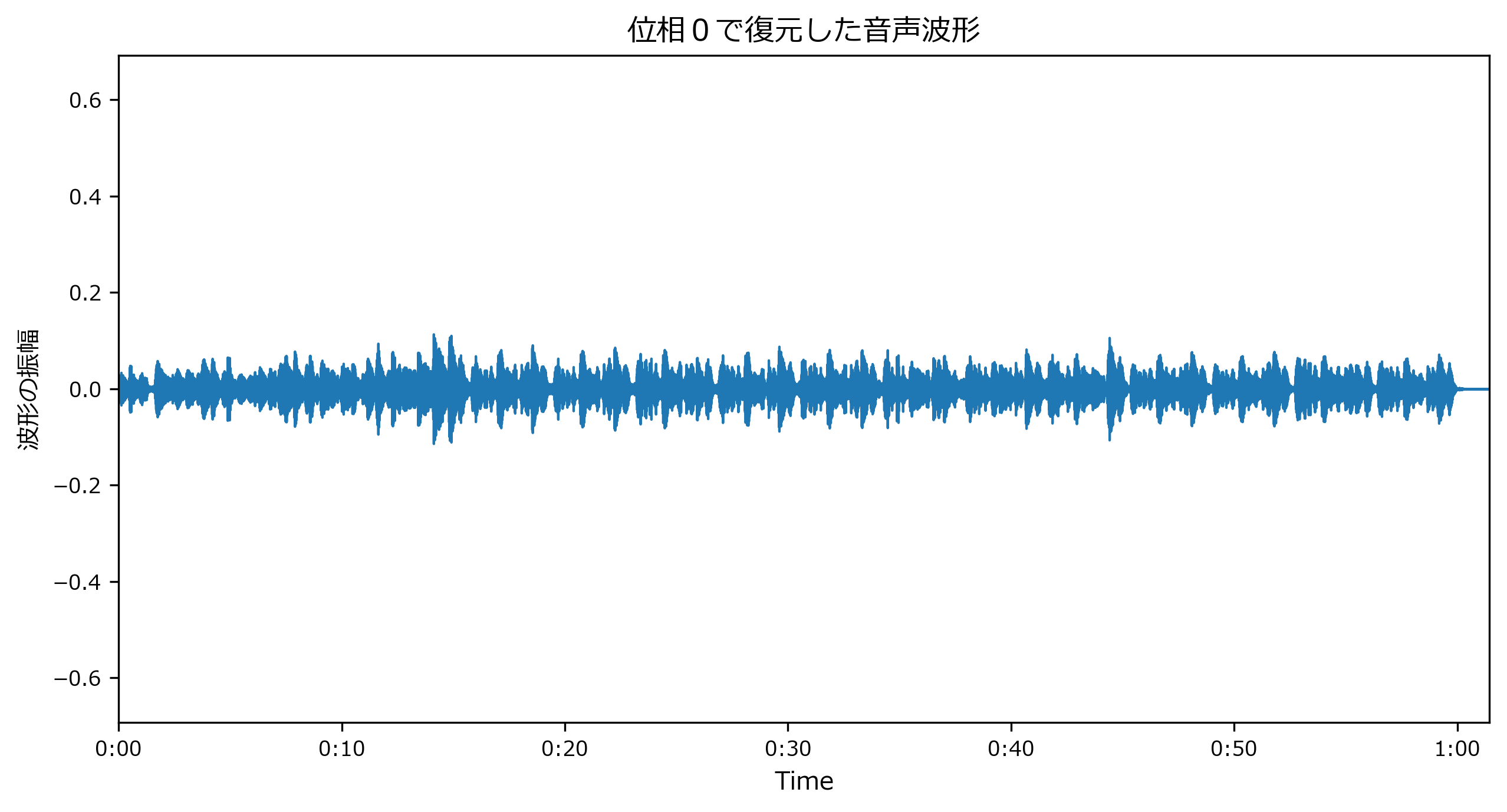
位相情報なしで復元した場合

位相をすべてゼロとして直交形式の複素数の行列Dへ変換した場合です。

D = S * np.exp(np.zeros(S.shape))
y_inv = librosa.istft(D)
display(IPython.display.Audio(y_inv, rate=sr))
mpl_collection = librosa.display.waveplot(y_inv, sr=sr)
mpl_collection.axes.set(title="位相０で復元した音声波形", ylabel="波形の振幅")
mpl_collection.axes.set_ylim(ylim);

librosa音声変換記事 https://t.co/CedmBGtHfS

Vibe Ace (Kevin MacLeod) / CC BY 3.0 pic.twitter.com/UzAxBfAFgt
— lilacs2039 (@lilacs2039) July 5, 2020

音声の振幅が小さくなっています。聞いてみても何かヘンです。

griffinlim()で位相推定した場合

librosa 0.7.x以降のバージョンではlibrosa.griffinlim()で、強度スペクトログラムのみから位相を推定して音声を復元できます。
- librosa.griffinlim() ドキュメント　https://librosa.org/librosa/master/generated/librosa.core.griffinlim.html#librosa-core-griffinlim
librosa 0.7.x　未満を使っているときは、issueから対象のソースコードをコピペして実行できます。（今回はこの方法です）
- Synthetic phase for inverse transforms #434
  - https://github.com/librosa/librosa/issues/434#issuecomment-291266229

def griffinlim(spectrogram, n_iter = 100, window = 'hann', n_fft = 2048, hop_length = -1, verbose = False):
    if hop_length == -1:
        hop_length = n_fft // 4

    angles = np.exp(2j * np.pi * np.random.rand(*spectrogram.shape))

    t = tqdm(range(n_iter), ncols=100, mininterval=2.0, disable=not verbose)
    for i in t:
        full = np.abs(spectrogram).astype(np.complex) * angles
        inverse = librosa.istft(full, hop_length = hop_length, window = window)
        rebuilt = librosa.stft(inverse, n_fft = n_fft, hop_length = hop_length, window = window)
        angles = np.exp(1j * np.angle(rebuilt))

        if verbose:
            diff = np.abs(spectrogram) - np.abs(rebuilt)
            t.set_postfix(loss=np.linalg.norm(diff, 'fro'))

    full = np.abs(spectrogram).astype(np.complex) * angles
    inverse = librosa.istft(full, hop_length = hop_length, window = window)

    return inverse

print("位相推定　開始")
y_inv = griffinlim(S, verbose=True)
print("位相推定　終了")
display(IPython.display.Audio(y_inv, rate=sr))
mpl_collection = librosa.display.waveplot(y_inv, sr=sr)
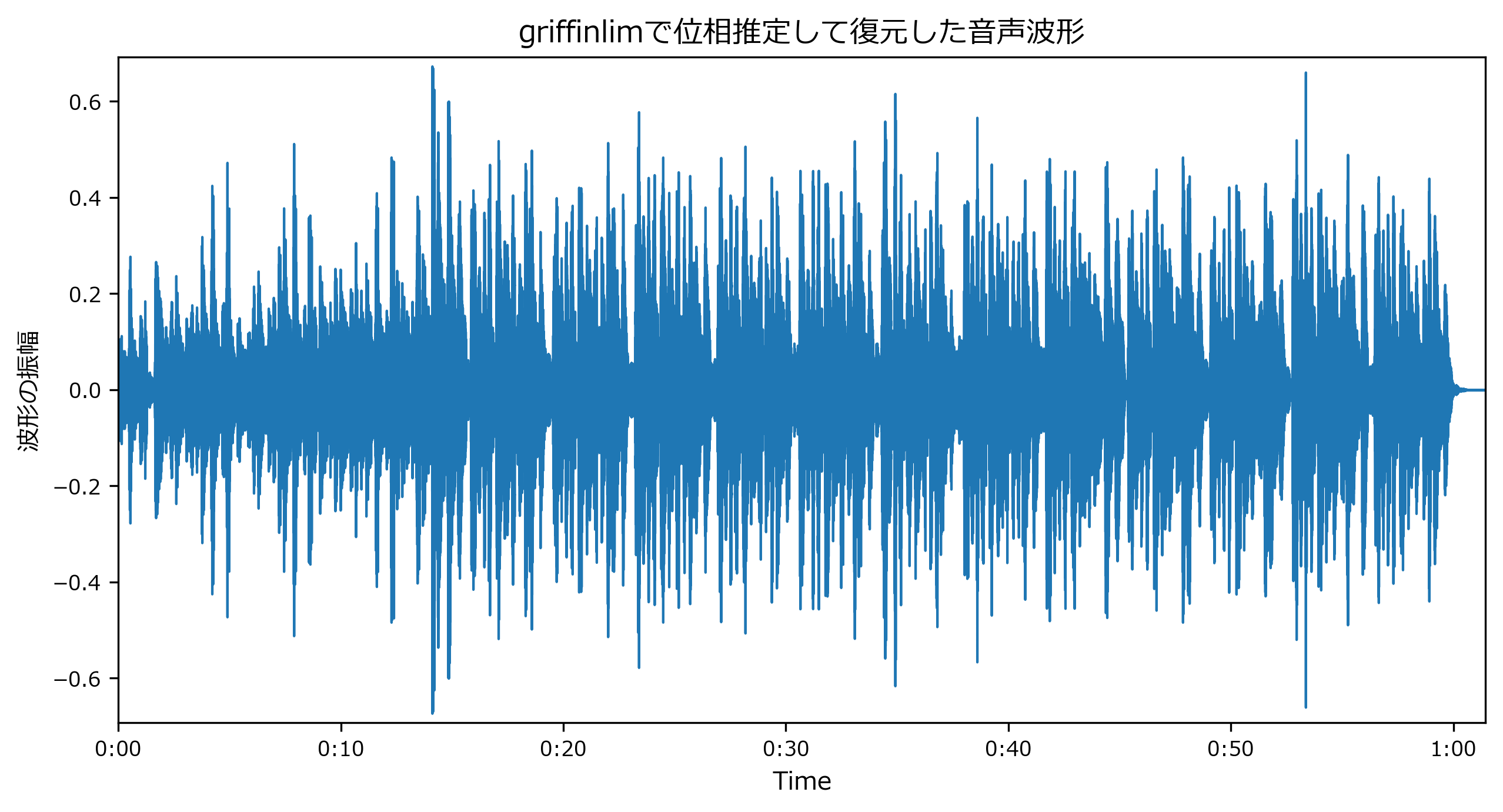
mpl_collection.axes.set(title="griffinlimで位相推定して復元した音声波形", ylabel="波形の振幅")
mpl_collection.axes.set_ylim(ylim);

出力

    位相推定　開始
    100%|███████████████████████████████████████████████████| 100/100 [01:04<00:00,  1.55it/s, loss=376]
    位相推定　終了

librosa音声変換記事 https://t.co/CedmBGtHfS

Vibe Ace (Kevin MacLeod) / CC BY 3.0 pic.twitter.com/k9M3LXCnGM
— lilacs2039 (@lilacs2039) July 5, 2020

復元結果
- 聞いた感じは遜色なく復元できています。
- 音声波形はよく見ると、元の音声とは少し異なっています。
使いどころ
- 音声認識モデルの学習のためにデータオーグメンテーションでホワイトノイズを載せるなど、スペクトログラムで音声を編集してから、位相を推定して音声を復元することで、編集後の音声を聞いて確認することができます。

まとめ

音声処理ライブラリLibROSAを使って、音声の読み込み　⇒　スペクトログラムへの変換　⇒　音声の復元をしました。

Vibe Ace (Kevin MacLeod) / CC BY 3.0 ↩

Pythonの音声処理ライブラリ【LibROSA】で音声読み込み⇒スペクトログラム変換・表示⇒位相推定して音声復元