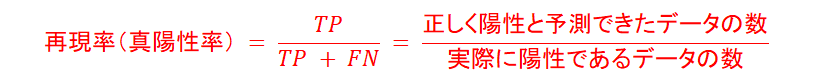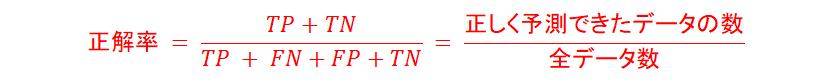そもそも、なぜ正解率だけではダメなの?
例えば病気の検査で、病気の人が全体の1%しかいない状況で、全員に陰性と診断すると正解率は99%になります。しかし、実際に病気だった人の見逃し率は100%なので良い予測とは言えません。
二値分類の評価では、正解率だけでなく病気の見逃しや誤検出も評価する必要があります。
前提
陽性と陰性は非対称である
二値分類では、積極的に検出したいものを陽性に割り当てることが多いです。検出したいものを陽性に割り当てると、検出の誤りに以下のような意味合いが出てきます。
- 検出したいのに検出できなかった → 見逃し
- 陰性なのに検出(陽性と判断)してしまった → 誤り
実問題では、見逃しと誤りの悪影響に差がある場合があります。
- 病気の検出タスクの場合
- 病気を見逃すことの悪影響が大きいです。病気を見逃した場合は、本当は病気であることを知る機会を長らく失うことになります。
- 逆に、誤って病気と判定した場合は、精密検査すれば対応できます。
- スパムメールの検出タスクの場合
- スパムではないメールを誤検出することの悪影響が大きいです。重要なメールを誤って除去した場合、一度もその重要なメールを見ることはありません。
- 逆に、見逃したスパムメールは手動で仕分ければ対応できます。
混同行列で全体を俯瞰
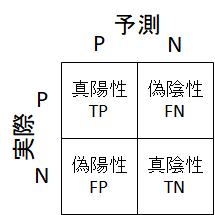
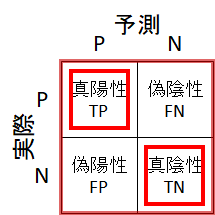
混同行列とは、データの予測結果を陽性・陰性ごとにまとめた行列です。分類タスクの性能確認によく使われます。この混同行列を使って説明していきます。
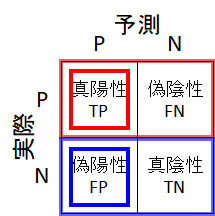
偽陰性(FN)⇒「見逃し」
偽陰性(False Negative:FN)のデータは、「実際は陽性だが、見逃してしまって陰性と判断したデータ」です。つまり、偽陰性(FN)は「見逃し」を意味します。病気の検出の例でいえば、実際は病気なのに、見逃してしまって健康と判断してしまったような場合です。

偽陽性(FP)⇒「誤り」
偽陽性(False Positive : FP)のデータは、「実際は陰性だが、誤って陽性と判断したデータ」です。つまり、偽陽性(FP)は「誤り」を意味します。スパムメール検出の例でいえば、スパムメールでない(=実際は陰性=必要なメールである)のに、誤検出して除去してしまったような場合です。
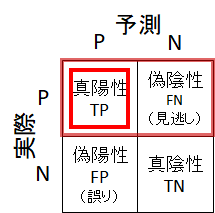
再現率(Recall)は見逃さない確率
以下は、再現率の計算式です。
- 式の意味は、「実際に陽性のデータのうち、見逃さずに陽性と予測できる割合(≒確率)」です。見逃しを意味する偽陰性(FN)を使って算出します。
- 逆にいえば、「見逃す確率 = 1 - 適合率」が成り立ちます。
- 予測の誤りがあっても「見逃さずに検出したい」ときは再現率を重視します。
- 例:病気の検出モデル
- 病気の誤検出があってもよいから、病気を見逃したくないので、再現率を重視します。
- モデルの再現率が0.99なら、すべての病気の人のうち、99%は検出できて、1%は検出できない、ということです。
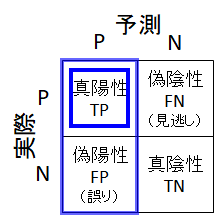
適合率(Precision)は誤検出しない確率
以下は、適合率の計算式です。
- 式の意味は、「陽性と予測したデータのうち、**誤検出ではなく実際に陽性である割合(≒確率)」**です。誤りを意味する偽陽性(FP)を使って算出します。
- 逆にいえば、「誤検出する確率 = 1 - 適合率」が成り立ちます。
- 多少の見逃しがあっても「誤検出を少なくしたい」ときは適合率を重視します。
- 例:スパムメールの検出モデル
- スパムメールを見逃してもよいから、誤検出して必要なメールを除去したくないので、適合率を重視します。
- モデルの適合率が0.99なら、スパムメールと予測したデータのうち、99%はスパムメールで、1%はスパムではないメール、ということです。
適合率と再現率の選び方
二値分類では、モデル(ロジスティック回帰など)が出力した予測値がしきい値を越えたら陽性と判断します。しきい値を決めるとモデルの予測(≒混同行列へのデータの振り分け)が確定するので、適合率と再現率も定まります。
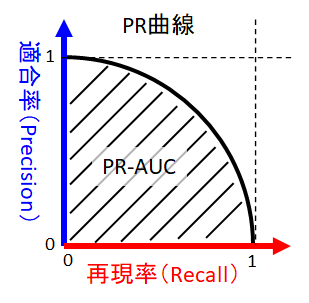
事前にすべてのテストデータの予測値を算出しておいて、しきい値を少しずつ変えたときの適合率と再現率の対応をプロットするとPR曲線が得られます。PR曲線の面積(PR-AUC)は、モデルそのものの良さを表す指標になります。
グラフから、再現率(見逃しの少なさ)と適合率(誤検出の少なさ)はトレードオフであることが分かります。モデルの学習が終わった後に、用途に適したしきい値を選ぶ必要があります。以下のような方法が考えられます。
- バランスを取る方法
- F1スコア(適合率と再現率の調和平均)が最大となるしきい値を選択
- 理想(適合率1, 再現率1)に最も距離が近いしきい値を選択
- どちらかを優先する方法
- 適合率が要件値(0.99とか)以上で、再現率が最大になるしきい値を選択
- 再現率 〃 適合率 〃
まとめ
- 偽陰性(FN)は「見逃し」を、偽陽性(FP)は「誤り」を意味する
- 再現率は見逃さない確率
- 適合率は誤検出しない確率
- 再現率(見逃しの少なさ)と適合率(誤検出の少なさ)はトレードオフ
- モデルの学習後に、用途に適したしきい値の選択が必要
そのほかの指標
正解率
真陽性率(TPR)・偽陽性率(FPR)
真陽性率(TPR):実際に陽性であるデータのうち、正しく陽性と判断できた割合
偽陽性率(FPR):実際に陰性であるデータのうち、誤って陽性と判断した割合
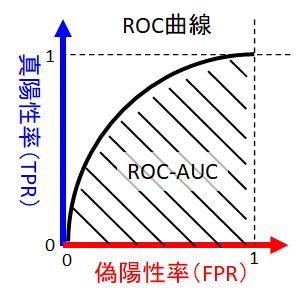
ROC曲線
真陽性率(TPR)と偽陽性率(FPR)の対応をプロットするとROC曲線が得られます。ROC曲線の面積(ROC-AUC)はモデルそのものの良さを表す指標になります。