1. 概要
化合物の物理的・化学的な性質を調べるために、NMR、液体クロマトグラフィ、赤外吸光などの測定が良く使われています。
これらの測定ではスペクトルデータを得ることができますが、たいていは意図しないノイズを含んでいます。
乾燥不十分で溶媒由来のドリフトがでたり、測定域の上下限でノイズがひどかったり、サンプル表面が不均一で散乱光成分が乗ったりと色々あるかと思います。
この記事では以下の工程により、汚い測定データを多少はマシなデータに変身させます。
・Asymmetric least squares smoother (Whittaker smoother)を用いたベースライン推定[1,2]
・Savitzky-Golay smootherを用いた平滑化[3,4,5,6]
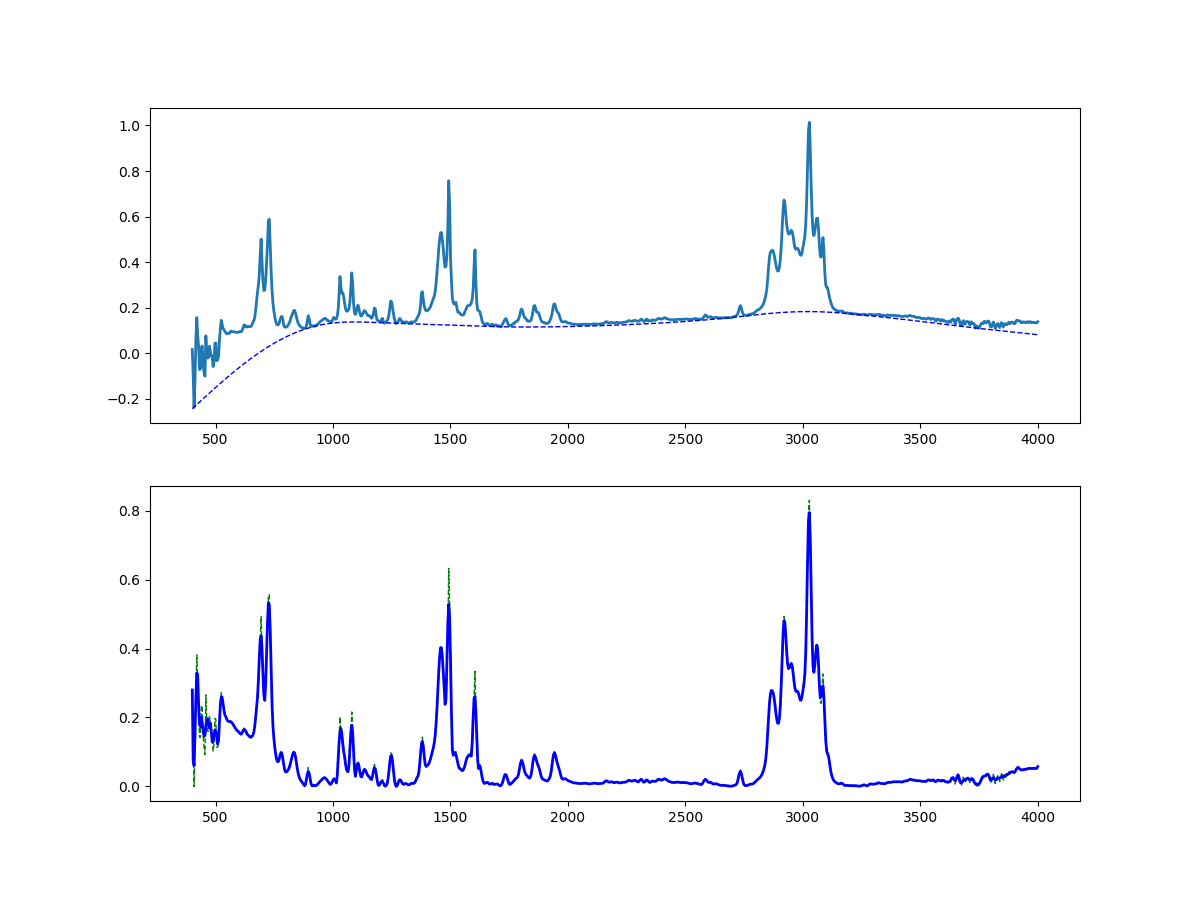
といいつつ、公開できる適当な失敗データでやって見たら(下図)ではうまくいかない場合もあるなという感じです。
この図は10年位前に取ったFT-IRのデータで、4-butyltriphenylamineをTBS保護したものを取ったやつだったと思います。
2. 理論とか
使っている手法の簡単な解説です、いらない場合は飛ばして次章までどうぞ。
数理モデルや経験則が不要で、人が引いたみたいなベースラインを引こうという方法を採用しています。
スペクトル分析への利用例としては、NMR[1,2]、ラマン[2,7]、FT-IR[2]、液クロ[2]、GC-MS[2]、MALDI-TOF-MS[2]、などが報告されてます。
実験し始めの手数で勝負な段階であたりをつけたりするに便利です。
特徴的なピークが何本かあるようなデータに対して特に有用ですが、ポリマーのFT-IRやXPSのワイドスキャンみたいなのにはあまり向かないかもです。
ちゃんとした報告に使えるかは、適応範囲を参照の上ご利用ください。
実際の手順を以下で説明していきます。
等間隔dの説明変数 $X$ に対し、測定値 $Y$ があるとします。
ここでベースライン推定値 $Z$、ベースライン除去と平滑化後の推定値 $\hat{Y}$ を求めています。
(手書きの汚い図で申し訳ないです、あとで修正すると思います)
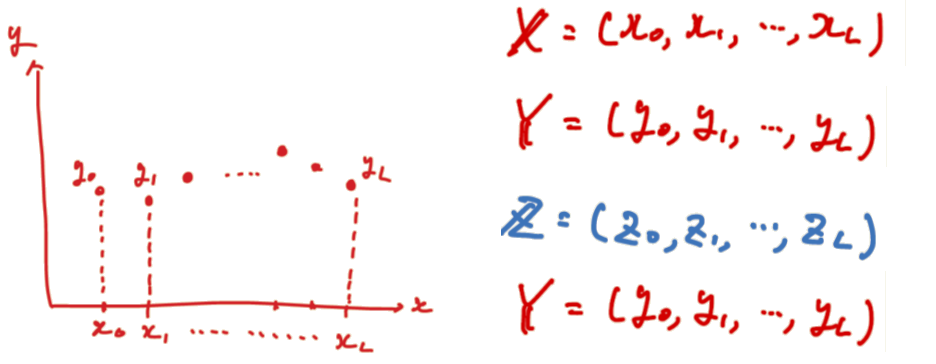
①ベースライン推定について
手法としてはAsymmetric least squares smoother(もしくはWhittaker smoother)というものです。
実装は参考文献[2]にMatlab版があり、疎行列使って軽くしたよという報告が[8]にあったのでまるまる使わせてもらっています。
Asymmetric least squaresでは罰則項をつけた最小二乗法で推定値$Z$を決定していきます。
リッジみたいな形ですが、罰則項の中身が異なります。
評価関数Fとしたときに
$F$ = (推定値の適合度合) + (推定値の平滑度合)
となるように中身を決めていきます。
・適合度合:
測定値と推定値の差をとりその二乗に重みを付けた値の和をとります。
差が負のときの重み $p$ 、正のときの重み $1-p$( $0 < p < 1$ )として重みを設定します。
・平滑度合:
推定値の$n$次導関数の二乗和により曲線の滑らかさを評価する(ここでは$n=2$)、この値のλ倍したものを罰則項として扱います。
(手書きの汚い図で申し訳ないです、あとで修正すると思います)
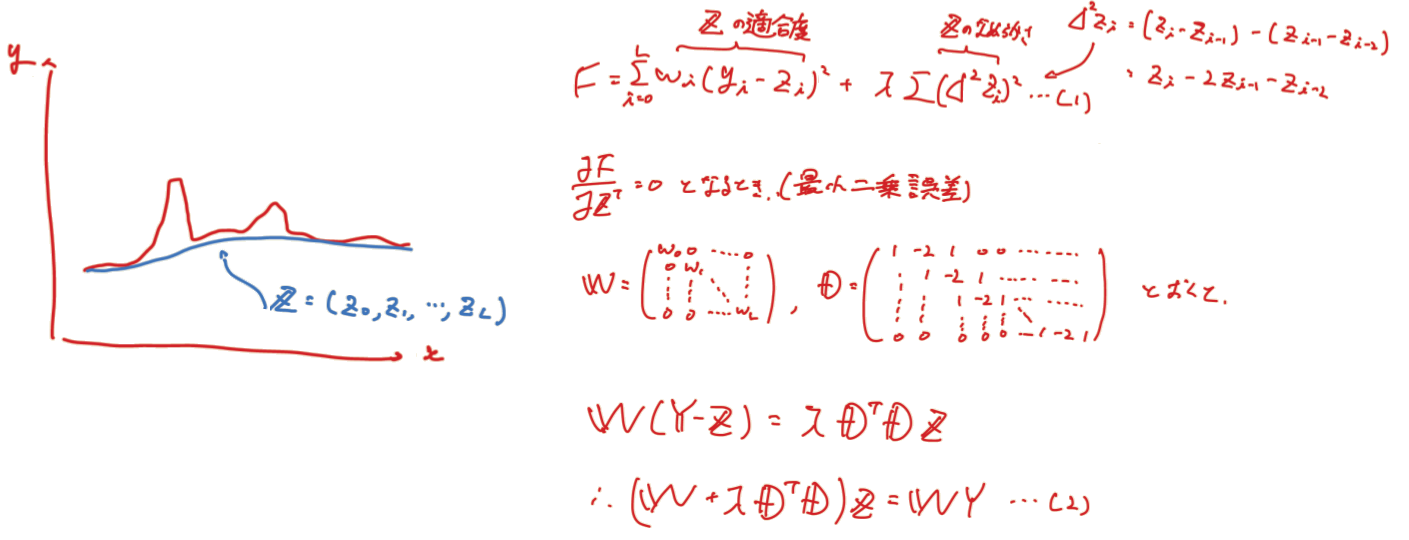
②平滑化について
一般的な多項式的合法(Savitzky-Golay法)を使っています。
実績ある方法でありかつ、微分しやすくピーク位置の特定やフィッティングなどへ発展させやすい方法であることが使用理由です。
Savitzky-Golay法では、ある説明変数$x_i$と測定値$y_i$があるとき、その値を中心とした近傍を含めた $2m+1$ 点が$n$次の多項式で記述できると仮定します。
ここで、$x_i$における多項式の値$\hat{y_i}$と測定値$y_i$の差分について最小二乗法を用いて、多項式の係数$A$を決めていきます。
説明変数は等間隔なので、選択した$x_i$との差をとり変数間の間隔dで割れば$±m$までの整数のみがのこります($u_i$とおきます)。
(手書きの汚い図で申し訳ないです、あとで修正すると思います)
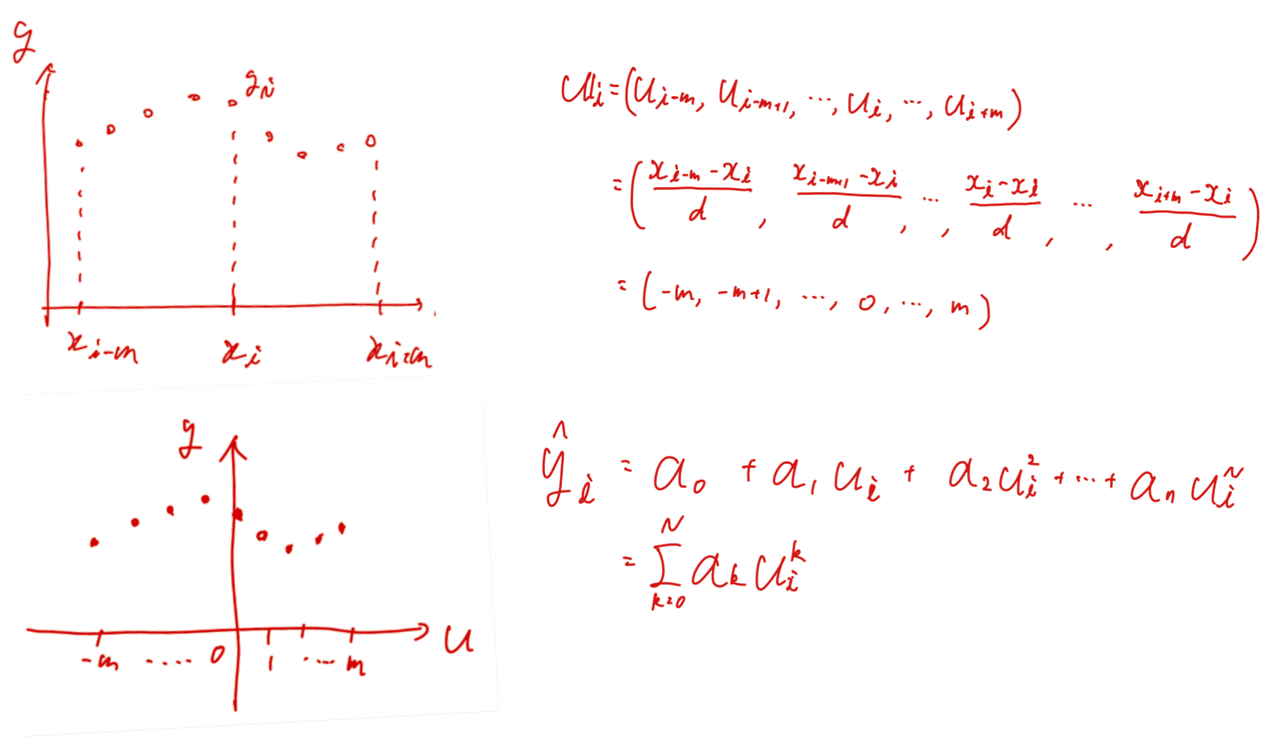
$i$の値を全域まで動かしていくと以下のような行列$U$とその関係式を得ることができ、推定値の計算と一致します。
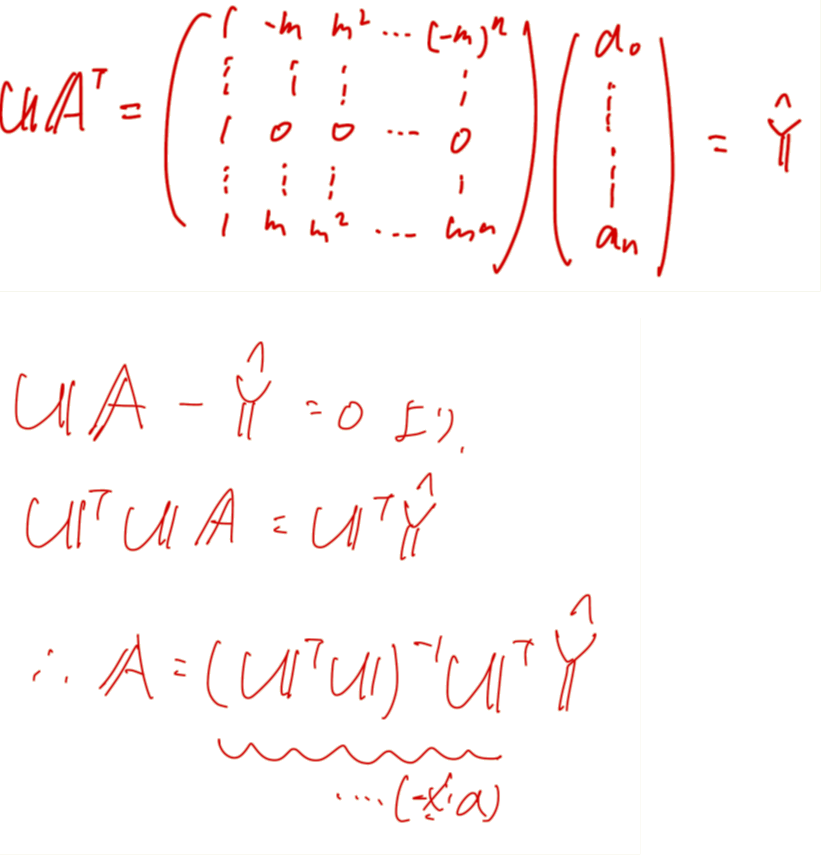
(※a)部の係数行列は簡単な形をしているため、窓の数と多項式次数によってあらかじめ計算できます。
Savitzkyらが詳細を報告しており、実際に係数表を使用して計算が実行されます。
3. 実装
カレントディレクトリにあるcsvファイルを読み込み、同ディレクトリにcsvを吐き出します。
読み込むcsvファイルは、A列に説明変数X、B列に測定値Yを入れたもの((A,B)=($X$, $Y$)と表記)にしてください。
吐き出すcsvファイルは、(A,B,C,D)=($X$, $Y$, $Z$, $\hat{Y}$)となります。
matplotlibの図もポップアップします。
コードは下記になります。
import csv
import numpy as np
from scipy import signal
import matplotlib.pyplot as plt
from scipy.sparse import csc_matrix
from scipy.sparse import spdiags
import scipy.sparse.linalg as spla
# パラメタを入力します、うまく推定ができないときはここをいじってください
# AsLSでのベースライン推定は ( W(p) + lam*D'D )z = Wy のとき、重み p と罰則項の係数 lam がパラメタです
# Savitzky-Golyでは、測定値をいくつに分割するかを dn で設定し(窓の数は len(Y)/dn になります)、多項式次数を poly で設定します
# paramAsLS = [ lam , p ]
# paramSG = [ dn , poly ]
paramAsLS = [10**3.5, 0.00005]
paramSG = [80, 5]
filename = 'testIR.csv'
# 測定データ(csv)を開きます
X = []
Y = []
with open(filename, 'r') as f:
reader = csv.reader(f)
data = [row for row in reader]
for i in range(len(data)):
X.append(float(data[i][0]))
Y.append(float(data[i][1]))
# AsLSによりベースライン推定を行います
def baseline_als(y, lam, p, niter=10):
#https://stackoverflow.com/questions/29156532/python-baseline-correction-library
#p: 0.001 - 0.1, lam: 10^2 - 10^9
# Baseline correction with asymmetric least squares smoothing, P. Eilers, 2005
L = len(y)
D = csc_matrix(np.diff(np.eye(L), 2))
w = np.ones(L)
for i in range(niter):
W = spdiags(w, 0, L, L)
Z = W + lam * D.dot(D.transpose())
z = spla.spsolve(Z, w*y)
w = p * (y > z) + (1-p) * (y < z)
return z
# Savitzky-Golyによりノイズ除去を行います
def SGs(y,dn,poly):
# y as np.array, dn as int, poly as int
n = len(y) // dn
if n % 2 == 0:
N = n+1
elif n % 2 == 1:
N = n
else:
print("window length can't set as odd")
SGsmoothed = signal.savgol_filter(y, window_length=N, polyorder=poly)
return SGsmoothed
# csvファイルと図を出力します
def outFigCSV(X,Y,paramAsLS, paramSG):
# baseline estimation and smoothing
Y_np = np.array(Y)
bkg = baseline_als(Y_np,paramAsLS[0], paramAsLS[1])
fix = Y_np - bkg
smth= SGs(fix, paramSG[0], paramSG[1])
# output
dataOutput = np.c_[X, Y, bkg, smth]
np.savetxt('output.csv', dataOutput, delimiter=',')
#figures
plt.figure(figsize=(12,9))
ax1 = plt.subplot2grid((2,2), (0,0), colspan=2)
ax2 = plt.subplot2grid((2,2), (1,0), colspan=2)
ax1.plot(X, Y, linewidth=2)
ax1.plot(X, bkg, "b", linewidth=1, linestyle = "dashed", label="baseline")
ax2.plot(X, fix, "g", linewidth=1, linestyle = "dashed", label="remove baseline")
ax2.plot(X, smth, "b", linewidth=2, label="smoothed")
plt.axis("tight")
plt.show()
# 実行します
outFigCSV(X,Y,paramAsLS, paramSG)
初めての記事で勝手がわからず、読みにくい部分だらけにも関わらず、ここまで読んでいただきありがとうございました。
ご指摘等々どんどんしていただけるとうれしいです。
4. 参考文献
[1]P.H.C.Eilers, Anal.Chem., 2003, 75, 3631-3636, 10.1021/ac034173t, A Perfect Smoother
[2]P.H.C.Eilers et al., Leiden University Medical Centre report, 2005, Baseline correction with asymmetric least squares smoothing
[3]A.Savitzky et al, Anal.Chem., 1964, 36, 8, 1627-1639, 10.1021/ac60214a047, Smoothing and Differentiation of Data by Simplified Least Squares Procedures.
[4]科学計測のための波形データ処理, 南茂夫, CQ出版株式会社
[5]N.Yoshimura et al., Journal of Computer Chemistry, 2012, 11,3, 149-158, 10.2477/jccj.2012-0007, Microsoft Excelを用いたケモメトリクス計算(5)
[6]R.W.Schafer, IEEE SIGNAL PROCESSING MAGAZINE, 2011, 111-117
[7]S.He et al., Anal.Methods, 2014, 6, 4402–4407, 10.1039/c4ay00068d, Baseline correction for Raman spectra using an improved asymmetric least squares method
[8]https://stackoverflow.com/questions/29156532/python-baseline-correction-library