この記事は、Akashic Engine Advent Calendar の8日目の記事です。
はじめに
Akashic Engine は JavaScript で動作するマルチメディアライブラリです。ニコニコ生放送で動くゲームの開発に使われています。Akashic Engine で何ができるかは以下の入門を読むと分かります。
Akashic Engine はとてもプリミティブな機能しか用意されておらず、例えば線を描く機能はありません。そこで前回 Akashic Engine に用意されている FilledRect を利用して線分を書く記事を書きました。
線が描けるようになると次は面を塗りつぶしたくなってきます。この記事では、Akashic Engine の FilledRect を利用して三角形を描く方法を説明します。前回に引き続き記事中のコードは TypeScript です。
CompositeOperation
Akashic Engine には CompositeOperation という機能が用意されています。CompositeOperationを利用すると描画をしたときに既存の描画と合成する方法を指定できます。
例えば以下のコードは色を変えた矩形を重ねて描画したものです。
const rect1 = new g.FilledRect({
scene,
cssColor: "#ff0000",
x: 200,
y: 100,
width: 300,
height: 200,
angle: 15
});
scene.append(rect1);
const rect2 = new g.FilledRect({
scene,
cssColor: "#0000ff",
x: 200,
y: 100,
width: 300,
height: 200
});
scene.append(rect2);
実行すると以下のように表示されます。
青い四角形に CompositeOperation の DestinationOut を指定すると以下のようになります。
const rect2 = new g.FilledRect({
scene,
cssColor: "#0000ff",
x: 200,
y: 100,
width: 300,
height: 200
});
実行すると、後から描画した領域が消えていることが確認できます。
FilledRect で三角形を描く
今回は CompositeOperation を使って、この描画した領域から不要な部分を消す機能を利用して三角形を描きます。(x1,y1), (x2,y2), (x3,y3) の3点で構成される三角形を作るには。全体を包み込む大きな矩形を書いて、そこから余分な部分を削ることで実現します。下の図では (a), (b), (c) が不要な領域になります。
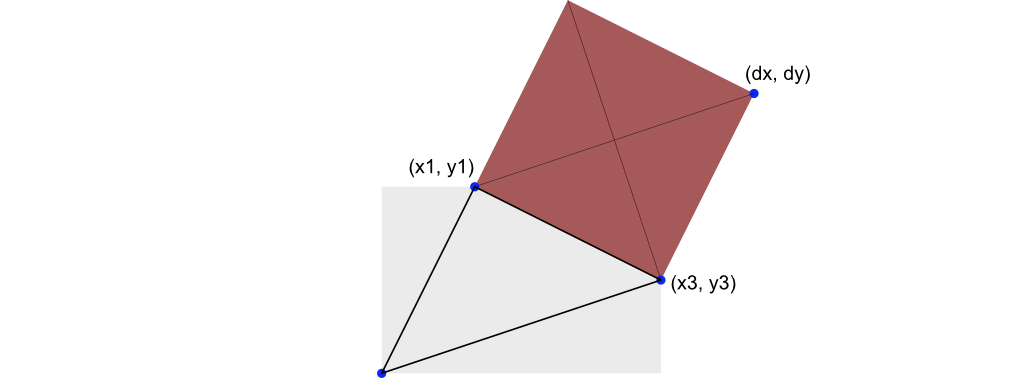
領域を削るには、削る部分を覆う矩形を作る必要があります。例えば (c) の部分を削る矩形は以下のように (x3,y3) と (x1,y1) の辺に接する矩形を作ります。
この矩形を作るのに必要な FilledRect のプロパティを計算していきます。まずはこの矩形のサイズですが、2点間の距離を一辺の長さとします。矩形は幅と高さを同じにして正方形で表現します。
const size = Math.sqrt(Math.pow(x3 - x1, 2) + Math.pow(y3 - y1, 2));
矩形の傾きは線分を描画した時と同様 atan2 で求めます。
const angleRad = Math.atan2(y3 - y1, x3 - x1);
Akashic Engine は矩形の中心を軸にして回転する都合上、矩形の中心座標を求める必要があります。中心座標を求めるために (x1, y1) の対角にある点 (dx, dy) の座標を求めます。
座標を求めるには三角関数を使います。 angleRad から Math.PI / 2 (直角) を引くと辺と直角な角度になります。
const dx = x3 + Math.cos(angleRad - Math.PI / 2) * size;
const dy = y3 + Math.sin(angleRad - Math.PI / 2) * size;
これで矩形の大きさを決めることができます。
const rect = new g.FilledRect({
scene,
cssColor: "#0000ff",
x: (x1 + dx - size) / 2,
y: (y1 + dy - size) / 2,
width: size,
height: size,
angle: angleRad / Math.PI * 180
});
ここまでのアイディアをコードにした結果が以下になります。
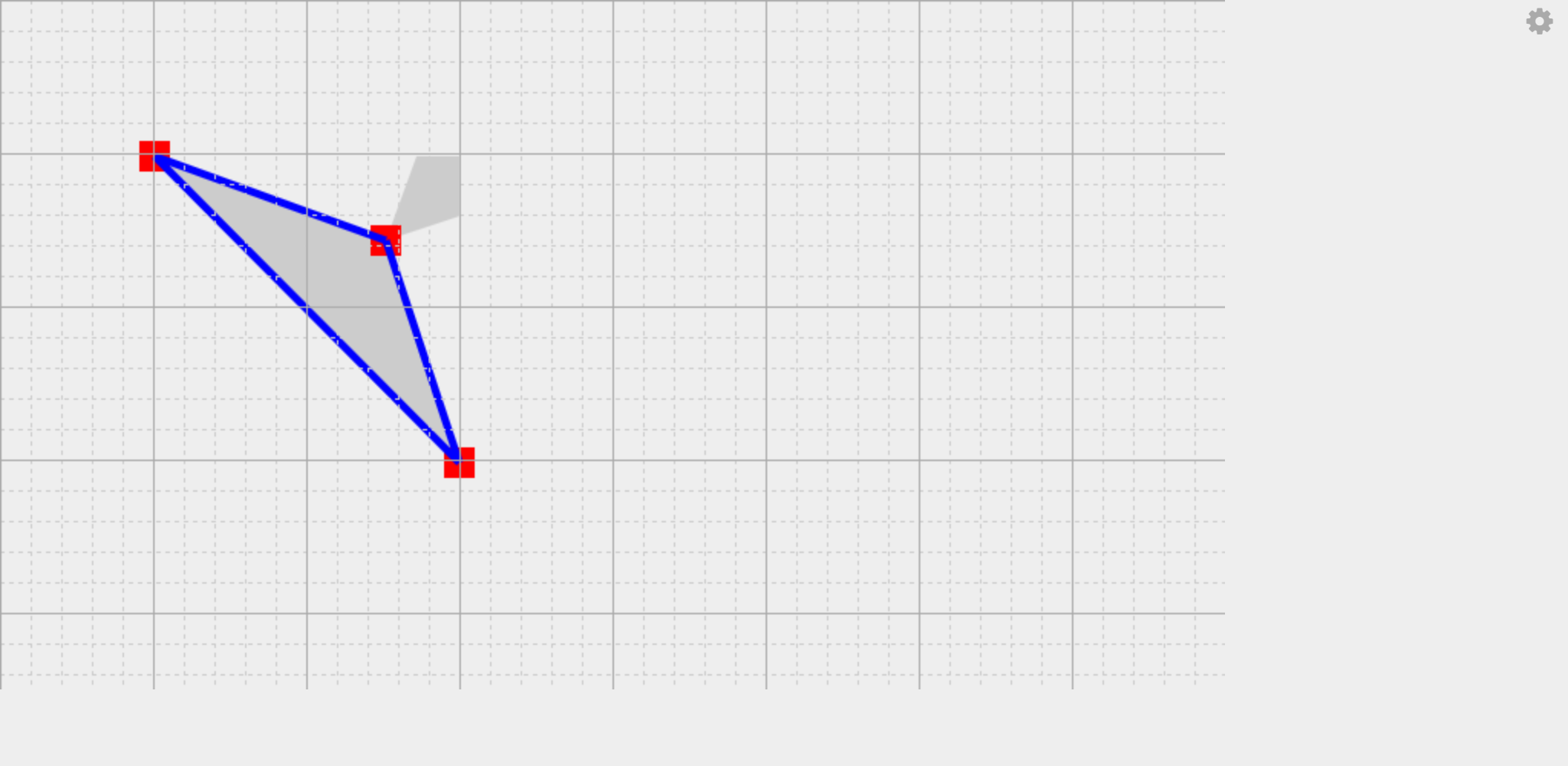
一見うまくいってそうですが、以下のような場合に不要部分をうまく切り取れていません。
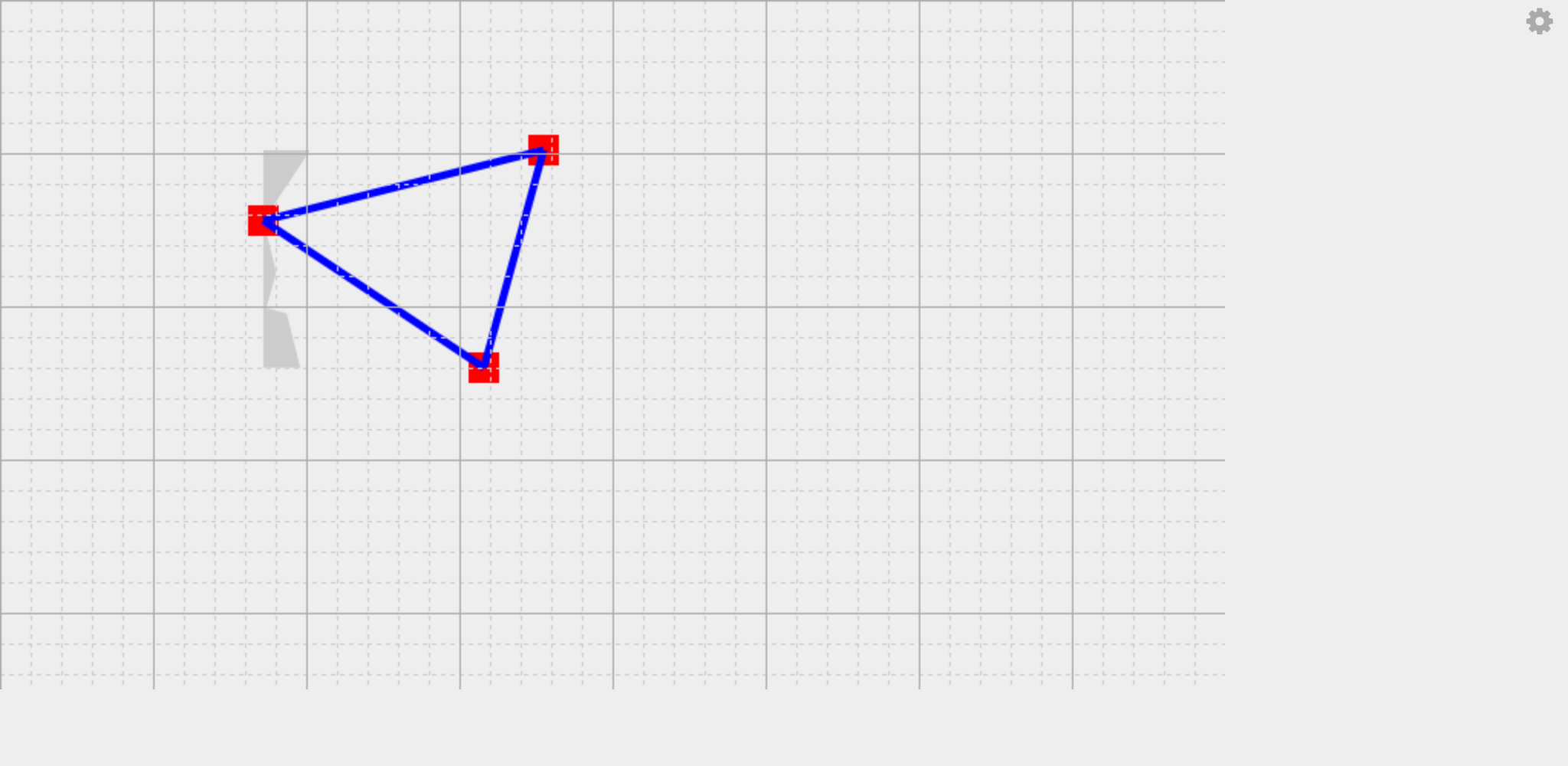
また頂点が反時計回りに並んでいない場合にも動きません。
最初の場合ですが、今回は各辺に接する正方形を書いているので以下のような場合にうまくいきません。
この問題は切り取るときの矩形の大きさを大きくすることで対応します。具体的には、width を2倍にします。
const rect = new g.FilledRect({
scene,
cssColor: "#0000ff",
x: (x1 + dx - size * 2) / 2,
y: (y1 + dy - size) / 2,
width: size * 2,
height: size,
angle: angleRad / Math.PI * 180
});
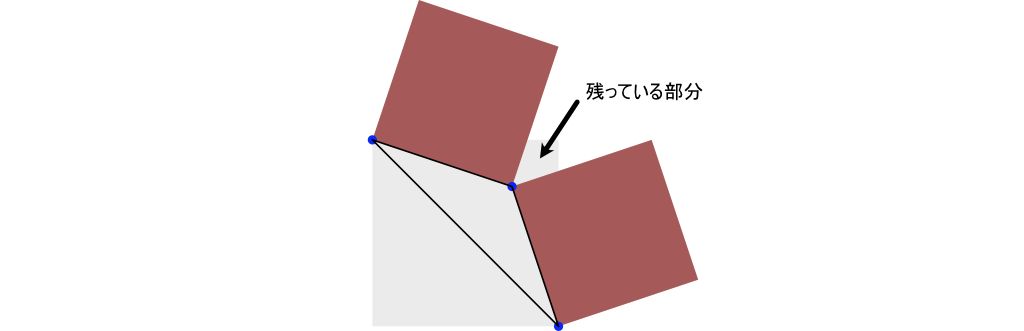
2倍の大きさにしましたが、このこれで本当に足りるのか考える必要があります。残っている場合が最も大きくなるのが、図のように22.5度、22.5度、135度の三角形になる場合です(なぜ22.5かはコメント欄に書きました)。ここの領域を埋めるのに必要な長さを辺の長さを1とすると、最大 (cos(22.5°) - sin(22.5°)) * sin(22.5°) = 0.207106... となります。今回は中心を変えずに大きさを二倍にしているので、左右両方に0.5ずつ増やしていると考えることができます。この値は 0.207106... よりも大きいので問題ありません。
2番目の頂点が反時計回りに並んでいない場合は、時計回りに並べ直して考えることにします。これについては面の裏と表を考えて、描画しないとしてもよさそうです。
デモとソースコード
以下のURLで実際に動くデモを試せます。
ソースコード全体は以下のリポジトリに置いてあります。