迷路の最短距離問題(BFS)〜Javascriptでの解法〜

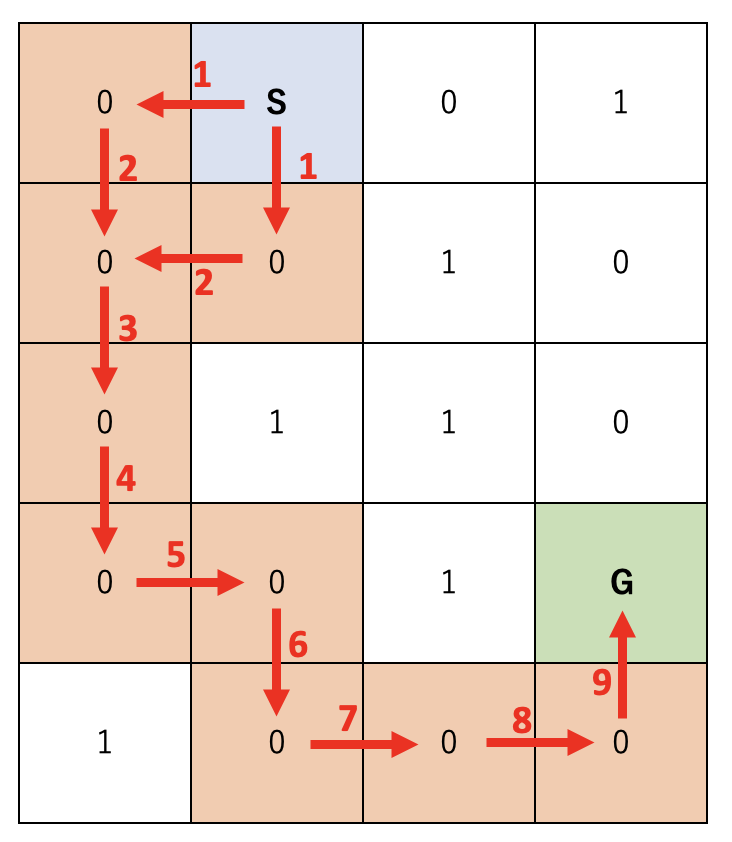
競技プログラミングでよく目にする迷路の最短距離問題。
この問題をJavascriptで解いてみたので備忘録として残しています。

まず、簡単にこの最短距離問題を紹介します。

問題

迷路にはスタート地点、ゴール地点と道、壁があり、スタートからゴールまでの最短距離を求める。
壁は貫通できず、道になっている箇所のみ通ることができる。

• スタート：S
• ゴール　：G
• 道 　：0
• 壁　：1

この問題でキーワードになるのが「BFS（幅優先探索）」です。
BFSの記事で分かりやすかったので参考にしました。
BFS (幅優先探索) 超入門！ 〜 キューを鮮やかに使いこなす 〜

BFSを簡単にいうと、探索開始元からの距離が近い方からしらみ潰しに探索していくアルゴリズムで、よく「DFS(深さ優先探索)」と対比されてます。
※DFSも簡単説明すると、一つのルートについて行き止まりまで一気に探索するアルゴリズム
個人開発で五目ならべの強化学習を作っていたのですが、何連続つながっているかを計算するときにDFSは使っていました。

この問題を解いてみると、最短距離は "9" となります。

コード

さっそくですが、Javascriptで実装したものです。

index.js

// tableにはsとgはもたせず、startとgoalに位置情報をもたせる
const start = [0, 1];
const goal = [3, 3];
const table = [
    ['0', '0', '0', '1'],
    ['0', '0', '1', '0'],
    ['0', '1', '1', '0'],
    ['0', '0', '1', '0'],
    ['1', '0', '0', '0']
];

const bfs = (start, goal, table) => {
    const dx = [0, 0 , 1, -1];
    const dy = [1, -1, 0, 0];

    let distance = -1; // 未到達:-1
    // スタート地点からの距離を保存する配列
    const distanceArr = deepCopy(new Array(table.length).fill(new Array(table[0].length).fill(-1)));
    distanceArr[start[0]][start[1]] = 0;

    // 探索済みマスを管理する配列
    const visitedArr = deepCopy(new Array(table.length).fill(new Array(table[0].length).fill(false)));
    visitedArr[start[0]][start[1]] = true;

    const queue = [start];
    while (queue.length > 0) {
        const q = dequeue(queue);
        const x = q[0];
        const y = q[1];

        // ゴールに到達
        if (x === goal[0] && y === goal[1]) {
            distance = distanceArr[x][y];
            break;
        }

        // 上下左右を探索
        for (let i = 0; i < 4; i++) {
            const nx = x + dx[i];
            const ny = y + dy[i];

            // テーブルの範囲内かつ道かつ未探索の場合
            if ((0 <= nx && nx < table.length) &&
            (0 <= ny && ny < table[0].length) &&
            table[nx][ny] === '0' &&
            !visitedArr[nx][ny]) {
                queue.push([nx, ny]);
                visitedArr[nx][ny] = true;
                distanceArr[nx][ny] = distanceArr[x][y] + 1;
            }
        }
    }
    return distance;
}

const dequeue = (queue) => {
    return queue.shift();
};

const deepCopy = (object) => {
    return JSON.parse(JSON.stringify(object));
};

解説

１. まず、上、下、右、左の位置の変化量を定義しておく。

const dx = [0, 0 , 1, -1];
const dy = [1, -1, 0, 0];

２. 距離を記録する配列を用意
スタート地点の距離を0で初期化

// スタート地点からの距離を保存する変数・配列
let distance = -1; // 未到達:-1
const distanceArr = deepCopy(new Array(table.length).fill(new Array(table[0].length).fill(-1)));
distanceArr[start[0]][start[1]] = 0;

初歩的なのですが、配列を用意するときに、fillで配列の初期値を詰めていくと、参照
渡しになってしまい途中で値を変更すると他の値も書き変わってしまいます。
私は無理やりDeepcopyしたのですが、無難にfor文でつくるのもありかもしれません。

３. 探索済みかどうかを管理する配列を用意
スタート地点は探索済みとしておく。

const visitedArr = deepCopy(new Array(table.length).fill(new Array(table[0].length).fill(false)));
visitedArr[start[0]][start[1]] = true;

４. 探索対象Queueを用意する
幅優先探索では対象の位置からその１つ移動できる位置を全てを探索対象としてQueueに入れます。
また、Start地点をQueueに入れておく。

const queue = [start];

↓↓↓ここからはwhile文の中身です↓↓↓

５. 探索対象を取り出す
これが基準点になり、ここから上下左右の探索をします。

const q = dequeue(queue);
const x = q[0];
const y = q[1];

６. ゴール地点が基準点になった場合は探索終了(while文を抜ける)

// ゴールに到達
if (x === goal[0] && y === goal[1]) {
    distance = distanceArr[x][y];
    break;
}

７. 上下左右の探索
nx、 nyは基準点から上下左右に移動した位置。
探索対象が見つかったら、

• Queueに入れる
• 探索済みフラグを立てる
• 基準点からの距離に+1したものを距離記録に残す

// 上下左右を探索
for (let i = 0; i < 4; i++) {
    const nx = x + dx[i];
    const ny = y + dy[i];

    // テーブルの範囲内かつ道かつ未探索の場合
    if ((0 <= nx && nx < table.length) &&
    (0 <= ny && ny < table[0].length) &&
    table[nx][ny] === '0' &&
    !visitedArr[nx][ny]) {
        queue.push([nx, ny]);
        visitedArr[nx][ny] = true;
        distanceArr[nx][ny] = distanceArr[x][y] + 1;
    }
}

ここでのポイントは、探索済みのものは探索しないことで大幅に計算量を減らすことができます。
グラフの頂点数を N、辺数を MとするとO(M)になります。

↑↑↑while文終了です↑↑↑

８. 最後に距離を返す
ゴールに到達してなければ、-1が返される。

return distance;

おわりに

私は情報系の出身ではないので、このBFSは競技プログラミングをやる中で初めて出会いました。競技プログラミングの中でアルゴリズムは様々ありますが、BFS以外のアルゴリズムにもぶち当たるので精進して参ります
これからも他のアルゴリズムについての解説や、苦しみながら作った五目並べのプログラムでたまたまDFSで実装している箇所があったりしたのでそこらへんも解説していければと思います。