今日は「みんなの医療統計 12日間で基礎理論とEZRを完全マスター!」(以下、新谷本)2日目の「仮説検定」の章を行います。
が、新谷本のこの章では特にRのスクリプトは書いていませんでした。
しかしながら「仮説検定」については「ベイズ統計モデリング―R,JAGS,Stanによるチュートリアル― 原著第2版」(以下、犬4匹本)では、二章建てで熱く語られていました。
今回は新谷本に加えて、犬4匹本11章(12章は新谷本4日目と一緒にやります)を見ながら、ベイズ流のアプローチでのプログラミングでの「仮説検定」も学習していきます。
仮説検定
取り合えず、2冊の本の違いをまとめますと
| 用語の定義など | 新谷本(2日目) | 犬4匹本(11章) |
|---|---|---|
| p値 | まぐれ当たりの確率 | 意図されたサンプリングや検定の手続きを用いるときに、仮定した母集団から実際以上に極端なサンプルの結果を得る確率 |
| 信頼区間 | 信頼区間とは、統計解析の結果がどれくらい信頼できるか、解析の精度を示した指標。使い方だけ押さえておく | 信頼区間は推定の不確かさを理解するための道具。ベイズのものの方が優れている |
| サンプリング分布の説明 | 同じ研究を異なる研究者が同数だが別の被験者を使って行った時のそれぞれの結果の集合(「統計理論上正しいと考えられている、机上の理論」) | 帰無仮説によって生成された仮想的な結果の集合(雲)。サンプリング分布に頼る統計方法は頻度主義者の方法 |
| 実験者の意図によるp値の変化ついて | サンプルサイズによってサンプリング分布が変わり、p値の値が変わってしまうことに言及 | サンプルサイズの違いに加えて、実験の停止の仕方によってもサンプリング分布が変わり、p値の値が変わることに言及 |
新谷本
はじめに新谷本2日目「仮説検定」をやります。
医療統計のエビデンスの鍵を握るp値とはどのようなものか
まぐれ当たりの確率であり、実際に得られたデータが帰無仮説を仮定したときにまぐれで起きるときの確率。
例えば、糖質制限ダイエットとカロリー制限ダイエットを比較したいときに糖質群で3人に2人が成功、カロリー制限ダイエットでは3人に1人が成功したとき、p値を計算すると1.0になった。すなわち、100%まぐれで起こったといえるのでこのデータを見ても「糖質制限ダイエットが効く」というエビデンスにならない。
今度は、糖質群で30人中20人が成功、カロリー制限ダイエットでは30人中10人が成功したとき、p値を計算すると0.02になった。すなわち、まぐれで起きるとしたら2%の確率で起こったと言え、なかなか起きるものではないので、「糖質制限ダイエットが効く」と解釈していいよ、すなわち「有意差が出た」というエビデンスになる。
「統計的な差」と「臨床的に意味がある差」を混同しない必要がある。
先の例でもわかる通り、p値は症例数が大きくなれば少なくなっていく。
ここで注意すべきなのは、p値は統計的に差がゼロかどうかを検定しているだけで、この差に臨床的な意味があるかどうかを検定しているわけではないことである。
症例数が多くなれば「統計的に有意差」は出るが、それは「臨床的に意味がある差」ではないこともある。
逆に、希少疾患等では患者数を十分担保できないため、効果の高い薬であってもなかなかマーケットに出すのは難しいという問題がある。(p値の性質による)
信頼区間
信頼区間とは、統計解析の結果がどれくらい信頼できるか、解析の精度を示した指標。これによって、「臨床的に意味のある差か」、本当の効果を見積もることが出来る。
症例数が多い場合は、信頼区間によって「臨床的に意味のある差」か数値的に判断でき、症例数が少ない場合は、「統計的な有意差が出ない理由」を差が原因なのか精度が原因なのか見積もることが出来る
信頼区間は使い方だけ覚えた方がいい
95%信頼区間がゼロ(差がない値)を含まない=統計的に有意差がある
筆者によると、上の使い方だけおさえるべきとのこと。
95%信頼区間は説明しようとすると混乱しますし、統計家が目くじらを立てて指摘するポイントなので、説明しようとはせず、その使い方だけおさえてください。
一応説明はあって、
よく間違えられるが、95%信頼区間は「95%の確率で真の値が入っている確率」ではない。
95%信頼区間とは、無数に存在する信頼区間のうち95%くらいには真の値が入っている区間。
例えば、同じ研究を異なる研究者が同数だが別の被験者を使って行ったとき、20回中19回は信頼区間に真の値が入っているよという区間。
(ただし、無数の研究者が同じ研究を行うわけではないのと一緒で、こんな区間が現実的に存在するわけではないので、これはあくまでも「統計理論上正しいと考えられている、机上の理論」)
犬4匹本
一通り、新谷本2日目で頻度主義の「仮説検定」について分かりました。
今度はベイズをやろうということで、新谷本2日目に対応する犬4匹本の章はどこか調べると、犬4匹本1章に読み方が書いてありました。
この辺り犬4匹本はすごい親切です。
もしあなたが帰無仮説を棄却したいだけならば...
大きさや不確かさの推定と対立して、伝統的な統計手法では、たびたび帰無仮説を棄却することに焦点が当てられる。帰無仮説におけるベイズ的な観点として、これらの章を読むこと。
第11章:伝統的な帰無有意仮説の有意性検定におけるp値の危険性について
第12章:空値(null value)の査定へのベイジアン・アプローチ
からの、11章冒頭
本章では、NHST(帰無有意仮説検定)の面白くもない詳細について説明し、上で述べたことに数学的な厳密さを与え、NHSTを完全に葬り去る。たとえデータが実験者の隠れた意図によって影響されないと仮定するとしても、実験車の隠れた意図はデータに関する決定にきわめて重要であるという考えを、NHSTがいかに求めているかを理解するだろう。
なるほど、先の新谷本の文章が回避性能において、いかに実践的かが分かる文章となっています。
統計家が目くじらを立てて指摘するポイントなので、説明しようとはせず、その使い方だけおさえてください。
帰無仮説有意性検定(NHST)におけるp値の定義
意図されたサンプリングや検定の手続きを用いるときに、仮定した母集団から実際以上に極端なサンプルの結果を得る確率
(=まぐれ当たりの確率by新谷本)
帰無仮説有意性検定(NHST)のp値の問題点
帰無仮説は仮想的な結果の集合(サンプリング分布)が必要。
(=同じ研究を異なる研究者が同数だが別の被験者を使って行ったときの結果。by新谷本)
しかしながら、サンプリング分布はデータのみからならず、データ収集者の意図(サンプリング時間や打ち止め方)によっても大きさが変わる。
特に、サンプリングの打ち止め方はデータのみからは分からないので、研究の意図が事前に与えられたものなのか事後に与えられたものなのか考えなければならない
打ち止め方でサンプリング分布が変わる例
ここから、犬4匹本の例を参考に同じサンプルサイズと結果でも、打ち止め方の違いでp値が変わることを確かめます。
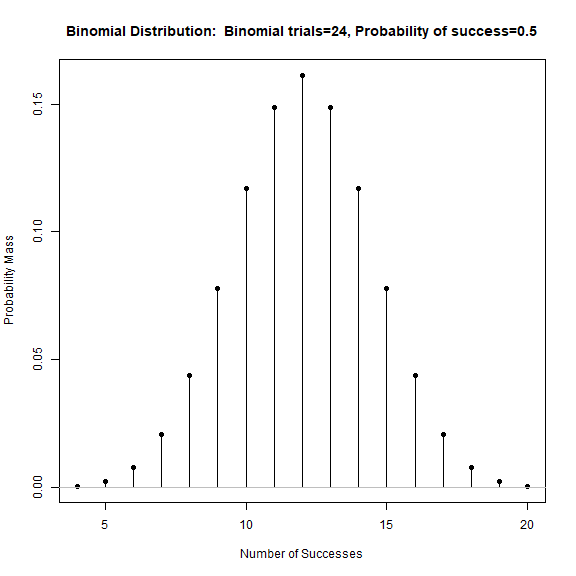
コインを投げた時、そのコインが曲がっているかを調べるために、帰無仮説(θ=0.5)、試行回数N=24、表の出た回数z=7で考えていきます。
> n <- 24
> z <- 7
> theta <- 1/2
試行回数N=24を固定したとき
サンプリング分布は2項確率分布になります。
確率分布のプロットはEZRの「標準メニュー」>「分布」>「離散分布」>「2項分布」>「2項分布を描く」から行えます。後の分布も同じように出力できます。
> local({
+ .x <- 4:20
+ plotDistr(.x, dbinom(.x, size=n, prob=theta), xlab="Number of Successes",
+ ylab="Probability Mass",
+ main="Binomial Distribution: Binomial trials=24, Probability of success=0.5",
+ discrete=TRUE)
+ })
> pbinom(z, size = n, prob = theta, lower.tail=TRUE)
p値もEZRから計算できます。「標準メニュー」>「分布」>「離散分布」>「2項分布」>「2項分布の裾の確率」で出力できます。
[1] 0.03195733
p値は0.032でした。両側検定では、2.5%以上なので有意差がありませんでした。
しかし…
表の出た数Zを固定したとき
表が7回出るまでサンプリングを行ったとき、サンプリング分布はどうなるか。
この場合、負の2項分布に従います。場所によって定義が異なりますが、今回の場合だと、目的の回数の数に試行が達したときを0回目として、その時に表が目的回数に達する確率の分布になります。
> local({
+ .x <- 0:100
+ plotDistr(.x, dnbinom(.x, size=z, prob=theta),
+ xlab="Number of Failures Until Target Successes", ylab="Probability Mass",
+ main="NegativeBinomial Distribution: Trials=7, Prob=0.5", discrete=TRUE)
+ })

この分布をもとに、出た結果がどれだけ極端かの計算を行います。
出来た分布が以下になります。
> .x <- 0:100
> plotDistr(z/(.x+z) , dnbinom(.x, size=z, prob=theta), discrete=TRUE)

左側は無限あるので、下の裾を取るために、有限回の右側の計算をしてから補集合を取るとp値が出ます。
> .x <- 0:(n-z-1)
> 1 - sum(dnbinom(.x, size=z, prob=theta))
[1] 0.01734483
p値は0.17でした。両側検定でも2.5%未満になり、有意差があるという結果になりました。
しかし、先ほどの例ではp値は有意差が無かったはずです。
停止のさせ方によって、p値の値が変わってしまいました。
時間を固定したとき
今度は時間を固定します。
1分間に平均1回コインを投げるとして、24分に固定して投げる場合、その試行回数はλ=24のポアソン分布に従うと考えられます。
そこで、各試行回数に対してポアソン分布による重み付けを施した2項分布を考えるとサンプリング分布が求まります。
ポアソン分布は以下のようになります。
> local({
+ .x <- 10:42
+ plotDistr(.x, dpois(.x, lambda=n), xlab="x", ylab="Probability Mass", main="Poisson Distribution: Mean=24", discrete=TRUE)
+ })

これを重みとして、2項分布を取ってプロットしたのが下になります。
> .x <- 0:42
> plot(seq(from = 0,to = 1, along.with = .x), seq(from = 0,to = 0.015, along.with = .x), type = "n")
> for (x in .x){
+ (0:x) %>%
+ dbinom(size = x, prob = theta) %>%
+ '*'(dpois(x, lambda = 24)) %>%
+ points((0:x)/x, ., col = rainbow(length(.x))[x+1])
+ }
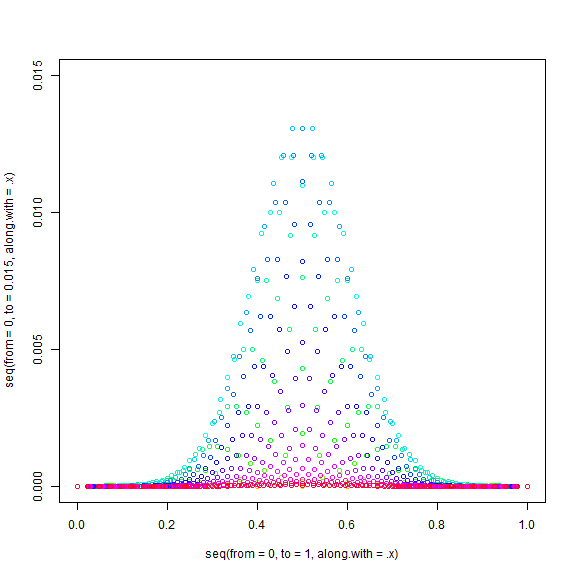
このp値を計算すると、
> .x %>%
+ sapply(function(x){
+ (0:x) %>% .[./x <= z/n] %>% max %>%
+ pbinom(size = x, prob = theta, lower.tail = TRUE) %>%
+ '*'(dpois(x, lambda = 24))
+ }) %>%
+ sum(na.rm = TRUE)
[1] 0.02379979
となり、p値として違う値が出ていることが分かります。
今回は両側検定で有意差有りとなりました。
試行回数を固定した場合と時間を固定した場合とで統計的な差の有意性が異なることは意外に感じました。
信頼区間について(頻度主義とベイズ主義)
信頼区間は推定の不確かさを理解するための道具
(=統計解析の結果がどれくらい信頼できるか、解析の精度を示した指標by新谷本)
- 頻度主義の信頼区間ではその目標は十分に達成されない。
- 頻度主義の信頼区間はp値の問題のいくつかを改善するが、p値の点から定義されるため、根本的にはp値と同じ問題に苦しむことになる。
- 帰無仮説によるサンプリング空間を仮定する必要があるため、信頼区間はやはり意図に依存する。
- 信頼区間は分布ではない(が、真の値との関係について容易にミスリードを引き起こす)
- ベイジアン分析ならその目標は十分に達成される。
- 最高密度空間(HDI)というのが頻度主義の信頼区間に対応するベイズ推論の概念
- 帰無仮説によるサンプリング空間を仮定しないため、HDIは意図に依存しない(観察することによって得られる結果に同意すれば)。
- 真の値について確信度という観点から直接解釈できる。
- 事前の信念に対して、新しいデータによってどの程度信念を変えるべきかが分かる。
後記
新谷本(黄)にはまだ3群以上の比較については書かれていなかったので、犬4匹本の多重比較については言及しませんでした。
「みんなの医療統計 多変量解析編 10日間で基礎理論とEZRを完全マスター!」(新谷本(ピンク))の方には書かれているみたいです。
犬4匹本のサンプリング分布のシミュレートについては3日目と関連しそうですが、今回の範囲を超えるため言及しませんでした。
今回の章を読むのに、新谷本(11ページ)は15分、犬4匹本(35ページ)は13時間ほど(多重比較、シミュレート周り除く)かかりました。参考にしてください。