「みんなの医療統計 12日間で基礎理論とEZRを完全マスター!」１日目

「みんなの医療統計 12日間で基礎理論とEZRを完全マスター!」１日目の「記述統計量」の章を読んだ後、独自で学習した際の記録を残す。
今回は特にベイズに関連する部分はない。

更新

• 20220716 引用部分と記事作成者の記述の違いが分かりづらいので修正。書評を追加。

書評

新谷本１日目「記述統計量」章

• 例を挙げながら、データの集団をいかに表すかを説明しており分かりやすかった。
• データの説明の際、どの記述統計量を使うべきかの説明をイラスト入りで説明しており頭に入りやすかった。

章キーワード

• 平均値
• 標準偏差と正規分布
• 分布と偏り
• ばらつき
• 中央値
• 四分位点

学習のメモ

• 指数との関係
• 記述統計量はKPIなどの指数の作成によく使われている気がするが本当にそうなのか調査
• 記述統計と標本分布の関係を確率分布の文脈で調べたい
• 記事作成者は記述統計量を使うよりも分布のグラフを出してしまう
• 記述統計と推測統計でいうところの前者の話

記事作成者の文章

記述統計量をEZRで出力する

記述統計量には平均値や標準偏差があるが、データの集団を表すには不十分なことが多い。
より正確にデータの情報を説明するためには、分位点など適切な記述統計量を利用することが重要。
これらについて、EZRを利用しながら学習していく。

EZRの出力レポート

以下の文章は、新谷本を参考にEZRのGUIを使っていくことで自動的に生成されたマークダウンファイルに追記を行ったもの。

<!-- R Commander Markdown Template -->

Replace with Main Title
=======================

### Your Name

### 2017-12-06

データセットとして、http://www.kspub.co.jp/download/1563148a.zip のデータを利用した。
糖尿病患者のデータで、おそらくアメリカのものと思われる。

> #####テキストファイルからデータを読み込む#####
> Dataset <- read.table("C:/EZRDATA/Datasets/1日目+5日目/DMRCT180.csv", 
+   header=TRUE, sep=",", na.strings=c("", "NA"), dec=".", fill=TRUE, 
+   quote="\"", strip.white=TRUE)

> library(tcltk, pos=15)

連続変数のコマンドを用いて記述統計量を算出する。

データ内で群間に分けて記述統計量を取ることがGUIでできるのでそれを利用した。

1　正規分布に従う集団の要約

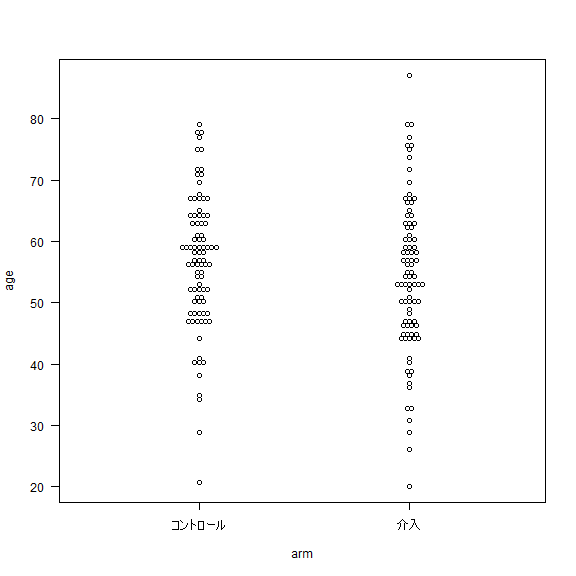
はじめに介入群とコントロール群で年齢の分布の要約を出力した。
今回は介入群とコントロール群で年齢の分布にそれほど大きな違いが無いことが分かった。
だいたい正規分布に従っていそうなことから、平均や標準偏差が記述統計量として利用しやすそうなことが分かる。

> #####連続変数の要約#####
> res <- NULL
> res <- numSummary(Dataset[,"age"], groups=Dataset$arm, statistics=c("mean", 
+   "sd", "quantiles"), quantiles=c(0,.25,.5,.75,1))
> colnames(res$table)[1:2] <- gettextRcmdr( colnames(res$table)[1:2])
> windows(width=7, height=7); par(lwd=1, las=1, family="sans", cex=1, mgp=c(3.0,1,
+   0))
> dot.plot(Dataset$arm, Dataset$age, xlab="arm", ylab="age")

> res

                 平均 標準偏差 0% 25% 50% 75% 100% data:n
コントロール 56.61798 11.04074 21  50  57  64   79     89
介入         54.08791 12.61802 20  46  54  62   87     91

2　正規分布に従わない集団の要約

次に介入群とコントロール群で罹患期間（年数？）について要約した。
これは罹患期間の短い人の多い山形の分布になっていることから、平均や標準偏差での記述に向かないことがわかる。

> #####連続変数の要約#####
> res <- NULL
> res <- numSummary(Dataset[,"dur_dise"], groups=Dataset$arm, statistics=c("mean",
+    "sd", "quantiles"), quantiles=c(0,.25,.5,.75,1))
> colnames(res$table)[1:2] <- gettextRcmdr( colnames(res$table)[1:2])
> windows(width=7, height=7); par(lwd=1, las=1, family="sans", cex=1, mgp=c(3.0,1,
+   0))
> dot.plot(Dataset$arm, Dataset$dur_dise, xlab="arm", ylab="dur_dise")

> res

                 平均 標準偏差 0% 25% 50% 75% 100% data:n
コントロール 8.584270 9.080209  0   1   5  12   36     89
介入         8.208791 9.302946  0   1   5  11   35     91

分割表の作成とその要約

介入群とコントロール群における男女間の割合の違いが無いか調べるため、分割表の作成を行った。
この場合、群数での比較になると分かりづらいので、割合に直してからの比較の方が適切。
結果から、介入群の方が男性が多いことが分かる。

また、症例数が40以上なのでカイ二乗検定を行った。

これは4日目の時の統計テストの選び方で説明がなされる（新谷本9日目も読む必要あり）。
20症例以下の場合はフィッシャーの正確確立検定を行うとのこと。

結果から、p値が0.4652なので、統計的な有意差はなさそう。このため介入群とコントロール群で男女比の差は問題ない程度であると考えられる。

> library(abind, pos=16)

> #####分割表の作成と群間の比率の比較(Fisherの正確検定)#####
> Fisher.summary.table <- NULL
> .Table <- NULL
> .Table <- xtabs(~arm+pat_gend, data=Dataset)
> .Table

              pat_gend
arm            女性 男性
  コントロール   38   51
  介入           34   57

> colPercents(.Table) # 列のパーセント表示

              pat_gend
arm             女性  男性
  コントロール  52.8  47.2
  介入          47.2  52.8
  Total        100.0 100.0
  Count         72.0 108.0

> .Test <- chisq.test(.Table, correct=FALSE)
> .Test

	Pearson's Chi-squared test

data:  .Table
X-squared = 0.5334, df = 1, p-value = 0.4652

参考

みんなの医療統計 12日間で基礎理論とEZRを完全マスター!