はじめに
コラッツ予想を逆向きに 1 から任意の自然数への経路を考える場合がある。その方法としてコラッツ予想式とは逆の計算、つまり数を2倍する、あるいは 1引いて3で割る操作を繰り返す方法を思いつくだろう。
本記事では逆経路に関する新たな方法(Journey Procedure)を記す。各々の自然数に対応する経路を計算するのではなく、経路の分岐点をまとめて数列として捉える方法である。
Journey Procedure
数列を生成する
Journey Procedure の原理は、最初の数列から新たな数列を生成し、生成された数列からまた新たな数列の生成を繰り返すというものである。
まず次の数列を与える
$JR(1)=1,2,4,8,16,...$
数列式で表すと以下のとおり。
$JR(1)⇒$
$a_1=1$
$a_n=2a_{n-1}$
これは 2 のべき乗の数列であり、第2項以降の数$(2,4,8...)$はコラッツ予想式(偶数の場合)を適用すればすべて 1 になる。
さて、この数列を基に別の数列を生成してみる。初見では意味が分からないかもしれないがまずは試してほしい。
生成元の数列。
$JR(1)=1,2,4,8,16,...$
これに初項として $0$ を追加する。
$0,1,2,4,8,16,...$
数列の偶数番目をマイナスにする。
$0,-1,2,-4,8,-16,...$
初項からの和を求め、それを新たな数列とする。
$0+(-1)=-1$
$-1+2=1$
$1+(-4)=-3$
$-3+8=5$
⇓
$-1,1,-3,5,-11,21,...$
新たな数列の偶数番目(正の数)をピックアップしたものを最終的な数列とする。これを $JJ(1)$ と表す。
$JJ(1)=1,5,21,85,341,...$
数列式で表すと以下のとおり。
$JJ(1)⇒$
$a_1=1$
$a_n=4a_{n-1}+1$
実はこの数列の任意の項は、3倍して1足すことで生成元の数列 $JR(1)$ のいずれかの項に戻る。
$5\times3+1=16$
$21\times3+1=64$
$85\times3+1=256$
これはつまり、以下のようなコラッツ予想における逆経路の生成を意味する。
JR(1)=1,2,4,8,16,...
⇓
JJ(1)=1,5,21,85,341,...
ちなみに $JR(n)$ は Journey Root, $JJ(n)$ は Journey Junction を表す。
さらに数列を生成する
さらに逆経路を生成できる。先に生成した $JJ(1)$ の項である $5$ を基に別の数列を生成してみる。まず
$JR(5)=5,10,20,40,80,...$
である。これは
$JR(5)⇒$
$a_1=5$
$a_n=2a_{n-1}$
の数列である。第2項以降の数$(10,20,40...)$はコラッツ予想式(偶数の場合)を適用すればすべて 5 になる。この数列を基に次の数列、つまりコラッツ予想の逆経路を生成する。
生成元の数列。
$JR(5)=5,10,20,40,80,...$
これに初項として $2$ を追加する(なぜ $2$ なのかは後で説明する)。
$2,5,10,20,40,80,...$
数列の奇数番目をマイナスにする(前の例では偶数番目だがこれは逆である)。
$-2,5,-10,20,-40,80,...$
初項からの和を求め、それを新たな数列とする。
$-2+5=3$
$3+(-10)=-7$
$-7+20=13$
⇓
$3,-7,13,-27,53,...$
新たな数列の奇数番目(正の数)をピックアップしたものを最終的な数列とする。これを $JJ(5)$ と表す。
$JJ(5)=3,13,53,213,853,...$
数列式で表すと以下のとおり。
$JJ(5)⇒$
$a_1=3$
$a_n=4a_{n-1}+1$
そしてこの数列の任意の項は、3倍して1足すことで生成元の数列 $JR(5)$ のいずれかの項に戻る。
$3\times3+1=10$
$13\times3+1=40$
$53\times3+1=160$
このようにコラッツ予想における新たな逆経路を生成できた。
JR(5)=5,10,20,40,80,...
⇓
JJ(5)=3,13,53,213,853,...
数列を生成できない例外
$JJ(1)=1,5,21,85,341,...$
$JJ(1)$ の項である $5$ からは $JR(5)$ を経て次の経路 $JJ(5)$ を生成できた。では $21$ はどうか? じつは $21$ からは次の $JJ(21)$ は生成できない。$JR(21)$ は存在するが $JJ(21)$ は存在しないのだ。
$JR(21)=21,42,84,168,336,...$
⇓
$JJ(21)=φ$
というのも $21$ は $3$ の倍数だからだ。$JJ(n)$ の $n$ が $3$ の倍数の場合、経路はそこで行き止まりである。実際 $3x+1$ の操作で $JR(21)=21,42,84,...$ のいずれかになる自然数は存在しない(たぶん![]() )。
)。
コラッツ予想の言い換え
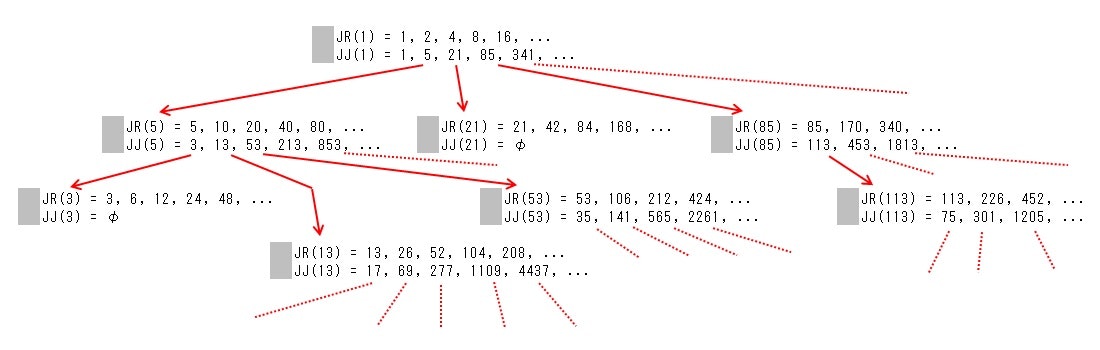
以上のように $JR(1)$ を出発点に数列の生成(Journey Procedure)を繰り返すと図のようになる。
生成された $JJ(n)$ の数列の任意の項は奇数なのだが、おそらく Journey Procedure で生成を無限に繰り返すと すべての奇数を重複なく生成できるのではなかろうか? これはコラッツ予想と同値な予想になり得るかもしれない。
Journey Procedure の一般式
$m$ を $3$ の倍数でない奇数とする。このときの $JR(m)$ から $JJ(m)$ を生成する一般的な方法を記す。
まず $JR(m)$ の数列は以下のとおり。
$JR(m)=m,\quad2m,\quad4m,\quad8m,\quad16m,\quad... $
つまり
$JR(m)⇒$
$a_1=m$
$a_n=2a_{n-1}$
このとき $m$ は次のどちらかで表せる($p$ は非負整数)。
$m=3p-1$
$m=3p+1$
.
この $p$ を $JR(m)$ の初項として追加する。
$p,\quad m,\quad2m,\quad4m,\quad8m,\quad16m,\quad... $
.
$m=3p-1$ の場合、奇数番目をマイナスにする。
$-p,\quad m,\quad-2m,\quad4m,\quad-8m,\quad16m,\quad... $
$m=3p+1$ の場合、偶数番目をマイナスにする。
$p,\quad-m,\quad2m,\quad-4m,\quad8m,\quad-16m,\quad... $
.
それぞれの場合で、数列の初項からの和を新たな数列とする。
$m=3p-1$ の場合。
$m-p,\quad-m-p,\quad3m-p,\quad-5m-p,\quad...$
$m=3p+1$ の場合。
$-m+p,\quad m+p,\quad-3m+p,\quad5m+p,\quad...$
.
さらに数列の正の数をピックアップしたものを最終的な数列とする。
$m=3p-1$ の場合。
$m-p\quad3m-p,\quad...$
$m=3p+1$ の場合。
$m+p,\quad5m+p,\quad...$
.
よって $JR(m)$ からの逆経路 $JJ(m)$ の数列式は最終的にこう表せる。
$JJ(m)⇒$
$a_1=m-p\quad(m=3p-1 の場合)$
$a_1=m+p\quad(m=3p+1 の場合)$
$a_n=4a_{n-1} + 1$
以上である。