はじめに
今日は勾配ブースティングについての投稿をしようと考えていたのですが、3ヶ月前に機械学習を学んで以降、大分知識が抜け落ちているなという印象を受けたので、今日から機械学習について一から勉強していくものにしていこうと思います。本日は正則化(Lasso回帰、Ridge回帰)を勉強した成果を挙げます。
正則化とは
trainデータには正確な予測ができるけど、将来のデータに対してはそれほどでもないというモデルの状態を過学習と呼び、このデータに対処するために正則化という作業を行います。実際に例を用いてやってみようと思います。
データ作成
データにはbostonデータセットを用います。これは、住宅価格を重回帰分析で予測するためのデータセットです。
# import文
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from numpy.random import *
from sklearn.linear_model import LinearRegression,Ridge,Lasso
from sklearn.datasets import load_boston
from numpy import linalg as LA
# bostonデータセットの準備
boston = load_boston()
# 説明変数の確認
columns = boston.feature_names
print(columns)
これにより、説明変数は
array(['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD',
'TAX', 'PTRATIO', 'B', 'LSTAT'], dtype='<U7')
であることがわかった。
説明変数ごとの日本語訳はこちら。
目的変数は'target'に格納されているので、
# df型で格納
data_x = pd.DataFrame(dataset.data,columns=dataset.feature_names)
data_y = pd.DataFrame(dataset.target,columns=['target'])
とした。
Ridge回帰、Lasso回帰の概要について
LPノルムについてはこちらのリンクを参照していただくとして、Ridge回帰はL2ノルムに罰則を課すものです。L2ノルムは以下の式で表されるもので、いわゆるベクトルの大きさを指します。
||w||_2 = \sqrt{(w_1)^2+(w_2)^2+ \cdot\cdot\cdot + (w_n)^2}
L1ノルムに罰則を課すLasso回帰について、こちらはL1ノルムに罰則を課すものです。L1ノルムは下記の式で表されます。
||w||_1 = |w_1|+|w_2|+ \cdot\cdot\cdot + |w_n|
LASSOは特徴選択による次元削減を自動的に行うことができます。サンプル数に対して特徴量が多い時に利用すると不要な特徴量を削減できます。
線形回帰、Ridge回帰、Lasso回帰の比較
では、実際に比較します。データ数が多すぎるのでデータ数を減らす処理をしています。
# インスタンス生成
lr = LinearRegression()
lasso = Lasso()
ridge = Ridge()
# データの削減
size = len(data_x.index) - 10
for i in range(size):
data_x = data_x.drop(i)
data_y = data_y.drop(i)
lr.fit(data_x, data_y)
lasso.fit(data_x, data_y)
ridge.fit(data_x, data_y)
## 図示
plt.plot(lr.predict(data_x), linestyle="solid",
color="black",label="lr")
plt.plot(lasso.predict(data_x), linestyle="solid",
color="red", label="lasso")
plt.plot(ridge.predict(data_x), linestyle="solid",
color="blue", label='ridge')
plt.title("lr, lasso, ridge")
plt.show()
これによる出力は下記の通りになります。Ridge回帰、Lasso回帰の順に過学習が抑えられているのがわかります。
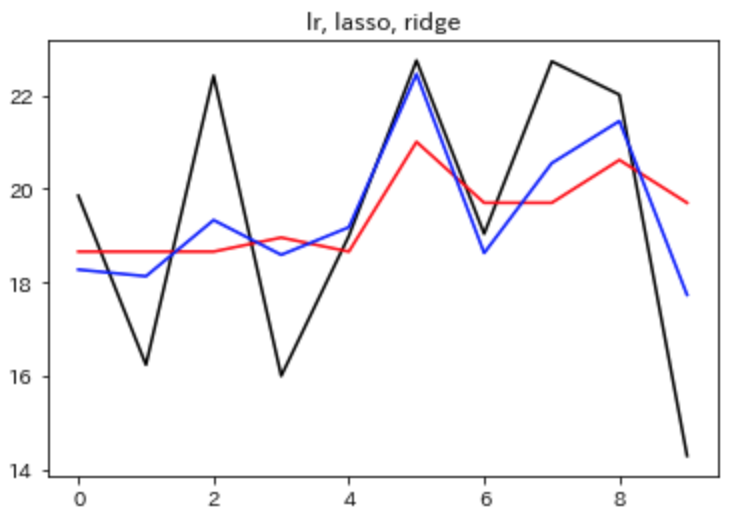
図だけでは影響の薄いとされる説明変数の重みが小さくなっているのか、本当にノルムが抑えられているのかわからないので、数字を出力して確認してみることにします。まず、重みを出力することにします。
# 正則化なしの時の重み
print(lr.coef_)
# Ridge回帰後の重み
print(ridge.coef_)
# Lasso回帰後の重み
print(lasso.coef_)
出力結果は以下のようになりました。
# 正則化なしの時の重み
array([[ 5.18970101e+01, -4.02455846e-13, 1.46033406e-03,
-2.02504680e-13, -7.82321821e-06, 7.36709552e+00,
-1.79320868e-01, -1.21591040e+01, -3.25967425e-03,
-7.69283122e-02, 1.17348273e-03, 2.47711678e-02,
6.75216061e-01]])
# Ridge回帰後の重み
array([[ 2.53025857e-01, 0.00000000e+00, -1.37577146e-05,
0.00000000e+00, 7.37020424e-08, 3.28166354e+00,
-2.43832964e-02, -1.18846289e+00, 3.07091843e-05,
7.24736750e-04, -1.10553064e-05, -4.45850693e-01,
1.99762992e-01]])
# Lasso回帰後の重み
array([ 0. , 0. , 0. , 0. , -0. ,
0. , 0. , -0. , -0. , -0.00883661,
0. , -0.26515107, -0. ])
このようにLasso回帰は次元削減を行うことが確認できました。では、続いて、L1ノルム、L2ノルムの値を確認してみます。
## 線形回帰とRidge回帰のL2ノルムを確認
print(LA.norm(lr.coef_, ord=2))
print(LA.norm(ridge.coef_, ord=2))
これにより、
53.81368022221476
3.533421125832272
と出力結果が得られ、Ridge回帰によるL2ノルムの縮小が確認できます。同様に
## 線形回帰とLasso回帰のL1ノルムの確認
print(LA.norm(lr.coef_, ord=1))
print(LA.norm(ridge.coef_, ord=1))
とすると
51.89701006427409
3.281663537382746
という出力結果が得られるので、Lasso回帰によるL1ノルムの縮小が確認できます。
まとめ
書くことないので省略。正則化について難しく思ってる人の助けになれたら嬉しいです。