機械学習の勉強をしているとL1正則化とかL2正則化という用語が出てくると思います。1
L1正則化の場合のペナルティ項:L1ノルムはこんな感じ、
という説明を見ますが、なぜL1ノルムとL2ノルムこんな形で表されているのか、をもうちょっとだけ掘り下げてみます。
Lpノルムの定義
ベクトル${\bf x}$をn次元、
$$
{\bf x} = (x_1, \cdots, x_n)
$$
としたとき、その時$L^p$ノルムは次のように定義されます。
\| {\bf x} \|_p = (\ |x_1|^p + |x_2|^p + \cdots + |x_n|^p )^{1/p}
L1ノルム
ここで、グラフに書けるように${\bf x}$を2次元としたときの$L^1$ノルムは
\| {\bf x} \|_1 = |x_1| + |x_2|
のように$x_1$と$x_2$のただの絶対値の足し算になります。それを等高線で表したものが
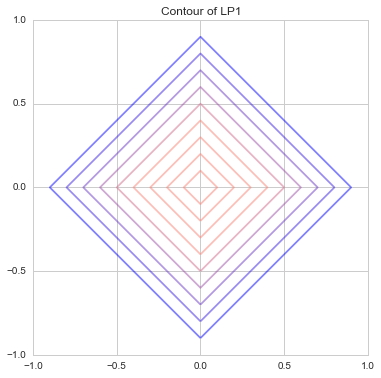
だったのです。これはマンハッタン距離とも呼ばれ、碁盤の目のように縦横垂直な道路しかないので、縦or横移動のみ可、斜めに移動できない、という世界の距離をあらわしているものと同じになります。
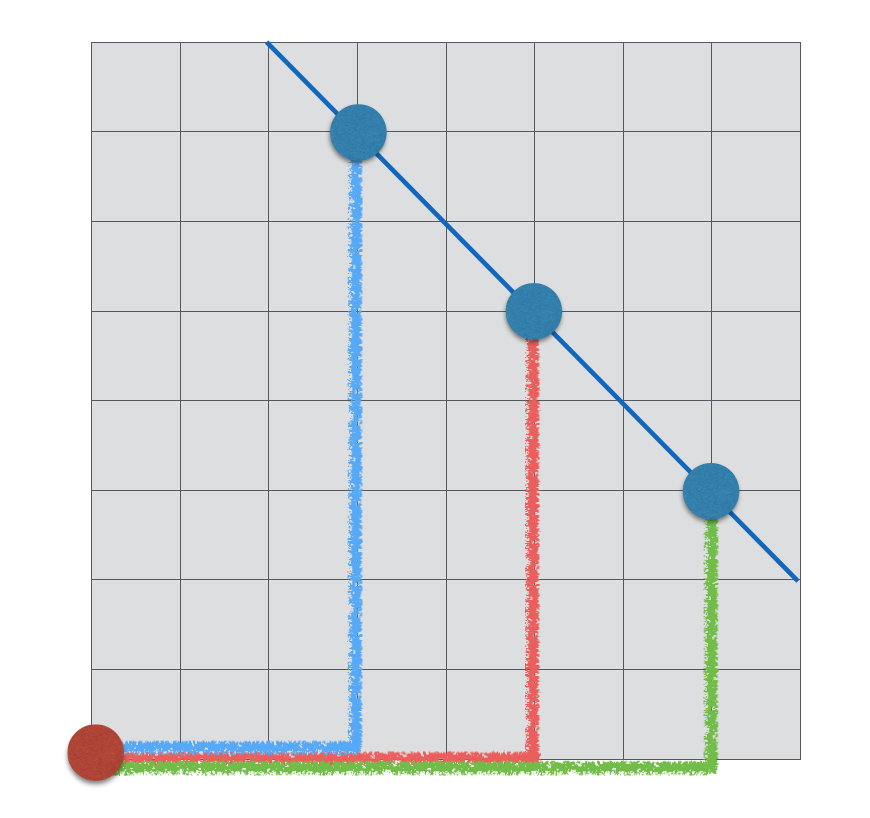
つまり、こんな感じで水色、赤、緑の線は全て長さ10なので、同じ距離のところを線で結ぶとこのように直線になります。なので先ほどのグラフの等高線がひし形になっているのですね。
L2ノルム
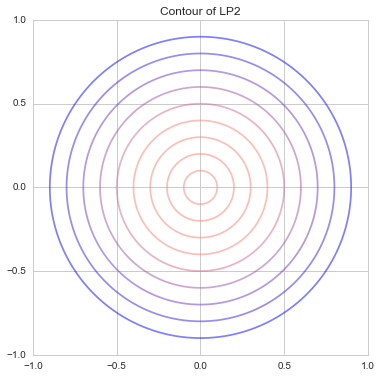
同じく2次元ベクトルの$L^2$ノルムは
\| {\bf x} \|_2 = \sqrt{|x_1|^2 + |x_2|^2}
です。これはおなじみのユークリッド距離です。円周上の点の原点との距離は常に一定なので、下記のような綺麗な円を描く等高線となります。
様々なpでのノルム
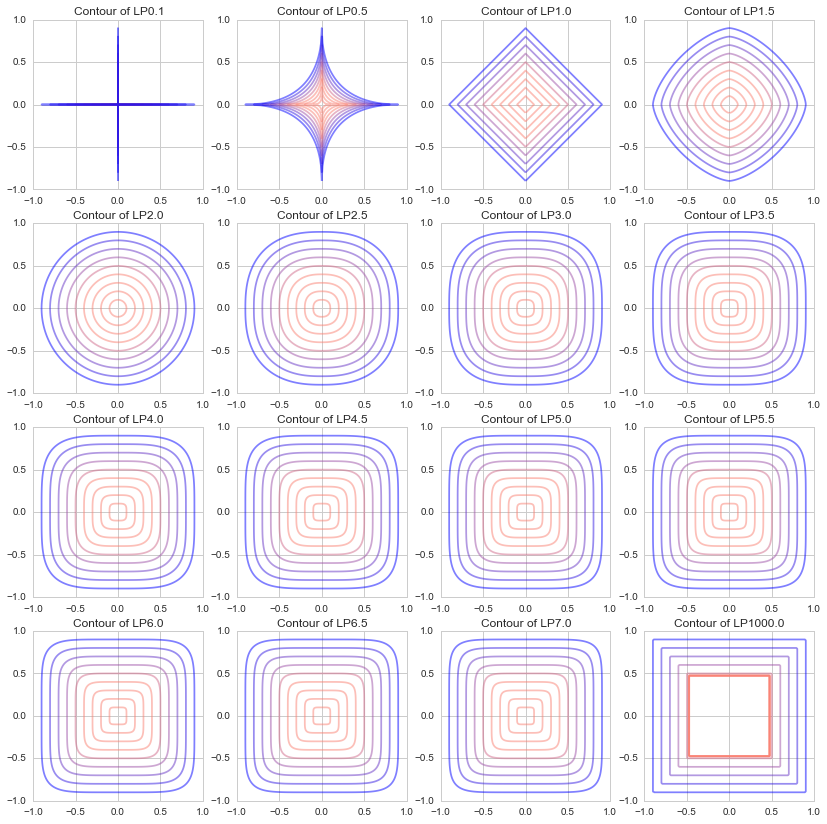
機械学習でよく使うのはL1ノルムとL2ノルムですが、理解のために様々なpの値でどのような等高線が描かれるのかを試してみました。
$p=0.1,\ p=0.5〜7.5$まで$0.5$ずつ、と、$p=1000$の図を描いてみました。
(本来Lpノルムの$p$は $p\ge1$の実数ですが、あえて0.1と0.5を描いてみました。)
pが0に近づくと"+"のような形に、1のときひし形(正方形を45度回転したもの)、2のとき円、∞に近づくと"□"のような形になることがわかります。
(Lpノルムの定義外ではありますがp=0.1の世界があったら、斜めに進むのがものすごく大変な世界です ![]() )
)
このようなL1ノルム、L2ノルムが応用されて、Lasso回帰、Ridge回帰、ElasticNetなどで使われているのですね ![]()
Pythonコード @GitHub
本記事のメイン部分のコードは下記になります。
def LP(x, y, lp=1):
x = np.abs(x)
y = np.abs(y)
return (x**lp + y**lp)**(1./lp)
def draw_lp_contour(lp=1, xlim=(0, 1), ylim=(0, 1)):
n = 201
X, Y = np.meshgrid(np.linspace(xlim[0], xlim[1], n), np.linspace(ylim[0], ylim[1], n))
Z = LP(X, Y, lp)
cm = generate_cmap(['salmon', 'salmon', 'salmon', 'salmon', 'blue'])
interval = [i/10. -1 for i in range(20)]
plt.contour(X, Y, Z, interval, alpha=0.5, cmap=cm)
plt.title("Contour of LP{}".format(lp))
plt.xlim(xlim[0], xlim[1])
plt.ylim(ylim[0], ylim[1])
# 16種のpの値のグラフを描画
fig =plt.figure(figsize=(14,14))
size = 4
for i, lp in enumerate(np.r_[[0.1], np.linspace(0.5, 7, 14), [1000]]):
plt.subplot(size, size, i+1)
draw_lp_contour(lp, (-1, 1),(-1, 1))
このグラフを描いたPythonコードの全文はGitHubに置いてあります。
https://github.com/matsuken92/Qiita_Contents/blob/master/General/LP-Norm.ipynb
参考
Wikipedia Lp空間
https://ja.wikipedia.org/wiki/Lp空間
オンライン機械学習 (機械学習プロフェッショナルシリーズ) [海野、岡野原、得居、徳永著]
http://www.kspub.co.jp/book/detail/1529038.html
RでL1 / L2正則化を実践する
http://tjo.hatenablog.com/entry/2015/03/03/190000
回帰モデルにおけるL1正則化とL2正則化の効果
http://breakbee.hatenablog.jp/entry/2015/03/08/041411
注釈
-
TJOさんの「銀座で働くデータサイエンティストのブログ」記事 RでL1 / L2正則化を実践する でも取り上げられています。 ↩