Grid Searchによる勾配ブースティングのハイパーパラメータ調整

はじめに

本日は以前に行ったJリーグの観客動員数予測のデータコンペの修正の続きに取り組んでいこうと思います。自分が初めて解いたときはこちら（修正後はこちら）
さて、前回は目的変数の正規分布化により、スコアを100程度縮めたわけですが、本日はコンペにて用いたGradient Boosting（勾配ブースティング）のハイパーパラメータ調整をGrid Search(グリッドサーチ)を用いて行うことにします。分類に比べて回帰にアンサンブル学習を用いる時の記事が少ないと感じたので回帰を題材とした記事を書いてみようと思います。

##Grid Searchとは？
さて本日利用するGrid Searchについて説明します。これはハイパーパラメータの値を適切なものに近づかせるために用いる手法です。その名の通りGrid(格子点)をSearch(探索)するものです。つまり複数のハイパーパラメータについて組み合わせを全て試し、最も評価精度の良いものを発見する手法です。SlideShareから取ってきた下図が非常にわかりやすいです。

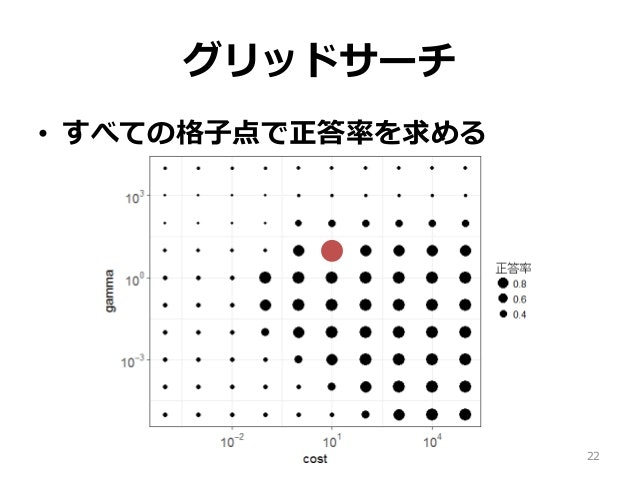
scikit learnにはGrid Searchを行う関数GridSearchCVがある。この引数は下図にて表される。

パラメータ名	説明
estimator	チューニングを行うモデル
param_grid	パラメタ候補値を「パラメタ名, 候補値リスト」の辞書で与える
n_jobs	同時実行数(-1にするとコア数で同時実行)
refit	Trueだと最良だったパラメタを使い学習データ全体で再学習する
cv	Cross validationの分割数(デフォルト値は3)
verbose	ログ出力レベル

##勾配ブースティングのハイパーパラメータの概要
勾配ブースティングはアンサンブル学習の一つで、ある決定木の間違いを修正するような決定木を逐次的につくることで､汎化性能の向上を目指すアルゴリズムです。最適化のために勾配降下法を用いることがその名の由来です。
さて、勾配ブースティングのハイパーパラメータは以下の通りです。 scikit learnの公式ドキュメントを参考に作りました。

パラメータ名	デフォルト値	説明
loss	ls	損失関数を最適化するもの {'ls', 'lad', 'huber', 'quantile'}から選択
learning_rate	0.1	合計でいくつの決定木を学習させるか。 n_estimatorsとトレードオフの関係
n_estimators	100	後に学習させる決定木が､前の決定木の間違いをどれだけ強く修正するか
subsample	1.0	各ステップの決定木の構築に関係するデータの割合。 1.0より小さいと確率的勾配ブースティングになる。
criterion	friedman_mse	分割の品質を測定する。基本的にデフォルト値が良い。
min_samples_split	2	内部ノードを分割するために必要なサンプルの最小数
min_samples_leaf	1	葉として必要なサンプルの最小数。 左右の枝分かれの葉がこの数より多いようにする
min_weight_fraction_leaf	0	min_samples_leafの割合表示
max_depth	3	各木構造の最大深度。 勾配ブースティングの特徴を反映させるには小さく設定するべき値。
init	None	初期予測を計算するもの
random_state	None	乱数のシード値の指定
max_features	None	最適な分割を探す際に考慮する機能の数 大きな値ほど過学習が起きやすい。 autoの時はmax_features=n_features sqrtの時はmax_features=sqrt(n_features) log2の時はmax_features=log2(n_features) Noneの時はmax_features=n_features
alpha	0.9	分位点回帰、Huber損失のα
verbose	0	1の場合は冗長出力を有効化する。
max_leaf_nodes	None	葉の個数の最大値、Noneを指定すると無制限になる。
warm_start	False	Trueで前のフィッティングに対して、追加ツリーをフィットさせる。
presort	auto	フィッティングを早めるために事前にソートを行うかどうか(boolかauto)
validation_fraction	0.1	早期停止のための妥当性確認として設定される訓練データの割合
n_iter_no_change	None	検証スコアが改善されない時に早期終了するかの決定
tol	0.1	早期終了のための許容差を決定する

##パラメータ調整
前回の点数は3,268.64733点で、これは勾配ブースティングのハイパーパラメータをデフォルトの値にしたものであり、このスコアを越すことを目標にしようと思いました。
import文は以下の通りです。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.grid_search import GridSearchCV
from mpl_toolkits.mplot3d import Axes3D
% matplotlib inline

1. n_estimators、learning_rateの調整

n_estimatorsは20~100で調整しlearning_rateは0.05~0.2で調整します。他パラメータはまず以下のように固定します。
min_samples_split = 5: 総サンプル数の0.5~1%が一般的、今回はデータに偏りがあまりないので5
min_samples_leaf = 50: 直感で選びます。過学習を防ぐ目的のためあまり小さな値を採用しません
max_depth = 5: サンプル数に応じて5~8ぐらいで選択。今回はデータ数が少ないので5
max_features = ‘sqrt’: 最初はsqrtが一般的
subsample = 0.8: 一般的な値

from sklearn.grid_search import GridSearchCV
from mpl_toolkits.mplot3d import Axes3D
#　ホールドアウト法
Xg_train_J1, Xg_test_J1, yg_train_J1, yg_test_J1 = train_test_split(X_J1, y_J1, test_size=0.3, random_state=0)
mod1J1 =GradientBoostingRegressor(
    min_samples_split = 5, 
    min_samples_leaf = 50, 
    max_depth = 5, 
    max_features = 'sqrt', 
    subsample = 0.8)
paramJ1_1 = {'n_estimators': list(range(20, 101, 10)),
             'learning_rate': list(np.arange(0.05, 0.20, 0.01))}
# scoringを neg_mean_squared_error(負のMSE)とする
gsearch1 = GridSearchCV(estimator = mod1J1, 
                        param_grid = paramJ1_1, 
                        cv = 5, 
                        n_jobs=4, 
                        scoring = 'neg_mean_squared_error')
gsearch1.fit(Xg_train_J1, yg_train_J1)
x = []
y = []
z = []
for i in gsearch1.grid_scores_:
    x.append(i[0]['n_estimators'])
    y.append(i[0]['learning_rate'])
    z.append(i[1])
fig = plt.figure()
ax = Axes3D(fig)
ax.plot(x, y, z)
plt.show()
# test精度の平均が最も高かった組み合わせを出力
print(gsearch1.best_params_)

この結果、

{'learning_rate': 0.19, 'n_estimators': 100}

と出力されました。Axes3Dによる図も出力したがよくわからないグラフになっていたので割愛します。
また、RMSEを確認するため

# そのときのtest精度の平均を出力(RMSE)
print((- gsearch1.best_score_) ** (1/2))
# ホールド・アウト法によるtest精度を出力(RMSE)
print((- gsearch1.score(Xg_test_J1, yg_test_J1)) ** (1/2))

と入力すると結果として

0.298537282383042
0.27801005403635193

と出力されました。

2. min_samples_splitとmax_depthの調整

min_samples_splitとmax_depthをともに3~7の自然数で調整します。上記とほぼ同様のコードを書くことで調整を行いました。すると

{'max_depth': 6, 'min_samples_split': 5}

と出力され、test精度の平均(RMSE)、ホールド・アウト法によるtest精度(RMSE)はそれぞれ

0.2942748176491349
0.2784377684697284

でした。　

####3. min_samples_leafの調整
続いて、min_samples_leafを1~71の10飛びの値で調整した。今回は変数が少ないためAxes3Dを用いずmatplotlib.pyplotを利用し、図を表示した。図は下記のようになる。

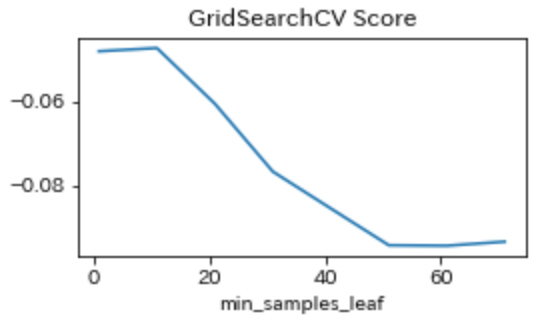
{'min_samples_leaf': 11}

と出力されました。ただ、グラフを見る限り1~11の間の値がmin_samples_leafに最適な値であるように考えられたのでmin_samples_leafを1~20の間で推移させ調整を行いました。図は下図のようになりました。

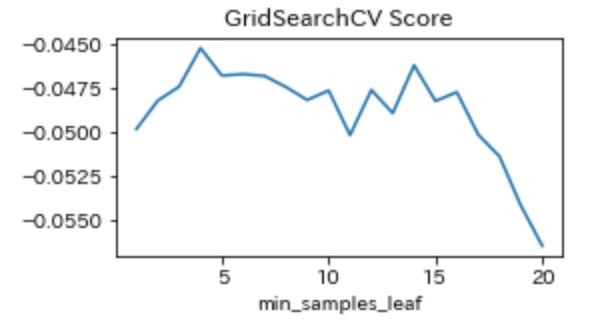
{'min_samples_leaf': 4}

またtest精度の平均(RMSE)、ホールド・アウト法によるtest精度(RMSE)はそれぞれ

0.2125592561762786
0.1994161961345939

でした。　

####4. max_featuresの調整
続いて、max_featuresを7~19の2飛びの値で調整した。

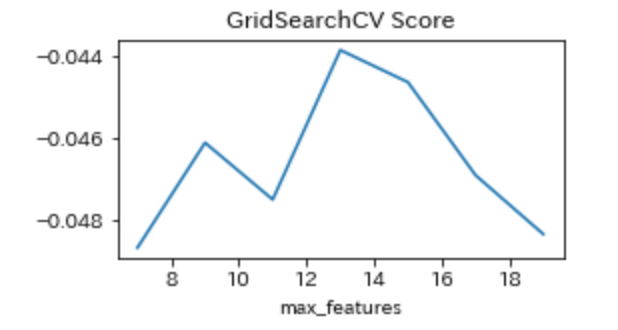
{'max_features': 13}

と出力されました。
またtest精度の平均(RMSE)、ホールド・アウト法によるtest精度(RMSE)はそれぞれ

0.20940111752331694
0.19811875953543406

でした。　
この手順でJ２リーグのデータも調整することで完了です。お疲れ様でした。
全コードはこちら

##まとめ
このGridSearchによるパラメータ調整の結果、Scoreが
3,268.64733点→3,245.83137点
と20点程度、スコアを伸ばすことができました。ちなみに順位は
62位/614位
でした。結構時間がかかった割にスコアが伸びにくいなと思いました。